Percentages
The purpose of this unit is to synthesise students’ fraction and decimal place value knowledge to enable them competently understand percentages.
- Recognise and demonstrate understanding of the relationship between fractions, decimals, and percentages.
- Use and explain percentage calculations (including with increase and decrease problems).
The ability to understand and work competently with percentages depends on the students having a sound understanding of place value, of our decimal number system and of fractions and their operations. It is important that students are given opportunities to explore, recognise, demonstrate and articulate these connections for themselves, and to be able to work fluently between them.
Relational thinking underpins the students' ability to understand that a percentage is used to express how large or small one quantity is in relation to another quantity (which is greater than zero). A percentage is a part to whole ratio.
Percent, from the Latin per centum literally means out of (per) one hundred (cent). The symbol % is made up of the / per sign and the two zeros (00) from the number 100. Therefore, a percentage can be thought of as a way of expressing a fraction of 100, another way of writing hundredths, and a new way of expressing the concept ‘out of 100’, using the % notation. It is important to use a range of physical representations to ensure that the students can clearly see and make the connections between the fraction: eg. 75/100 (or 3/4), percentage 75% and decimal representation 0.75 of the same amount.
Having a sound decimal place value understanding underpins the students’ ability to work with percentages. With this understanding a student can readily see, for example, that 0.6 is 6 tenths, is also 60 hundredths and is therefore 60%, whilst 0.06 is 6 hundredths and is therefore just 6%. Students will come to recognise the advantages of working with decimals rather than fractions when converting to percentages, particularly when the ratio cannot be represented as a common fraction.
Building a ready knowledge of common equivalent fractions for percentages, (1/4 = 25%, 1/2 = 50%, 3/4 = 75%, 1/10 = 10%, 1/5 = 20%, 1/8 = 12.5%), being able to use these as benchmarks to work out some other percentages (eg. 15% = 10% + half of 10%) and simplifying fractions and expressing these as percentages (eg. 9/36 = 1/4 = 25%) and are key outcomes. Using a formula to calculate a percentage requires an understanding of what is happening: the numerator of a fraction is divided by the denominator giving a decimal fraction which is then multiplied by 100 to express a percentage. For example, 72/120 x 100/1 = 0.6 x 100 = 60%. This can also be thought of as 6/10 of 100, which is of course 60.
As in any mathematics, estimating skills are important. Students should anticipate what answer would be reasonable. For example, if asked to find 9% of 450, a student should understand that they could find 10%, which is 45, and 1%, which is 4.5, and suggest that 9% will therefore be close to 40.
In responding to problems related to percentage increase or decrease the student must understand what the percentage is relative to. For example, an increase of 100% means that the final amount is 200% of the original amount, whilst a decrease of 100% means that the final amount is zero. Care must be taken in calculating percentage change. If, for example, the price of $50 were increased by 10% it would go up by $5 to $55. If it were then reduced by 10% it would go down by 10% of $55, or $5.50, resulting in a price of $49.50. The two changes here are relative to different quantities.
Calculating percentage change can be challenging when problems involve reverse percentages. For example, when finding the original price for an item for which you paid $15 following a discount of 25%.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- providing small group teaching opportunities to allow ākonga to consolidate different concepts
- providing digital representations of percentages, decimals, and fractions
- providing opportunities for tuakana-teina (peer learning) to allow ākonga to support and teach each other
- simplifying the complexity or quantity of percentages, fractions, and decimals ākonga are expected to work with in a session
- allowing the use of calculators for ākonga to check and support mental calculations.
These ideas are presented in five sessions, however, as the sessions include complex concepts that are fundamental to success with fractions, they can be extended over a longer period of time.
Whilst games are introduced and used within sessions to consolidate ideas, they can also be added to the class or group independent activities, or be sent home for whānau challenges and enjoyment.
The contexts for this unit can also be adapted to suit the interests, experiences, and cultural makeup of your students. The unit includes contexts such as sports games, kai and voting. You could work with the students and whānau to change these suggested contexts to instead link them to meaningful contexts from their lives. Other possible contexts involving percentages could include a marae visit, fundraising event, a fiefia night, or preparing a hāngī. Students could also collect examples or percentages from school data, CensusAtschool information, advertising material and from the media (newpapers, online). This will help them realise just how frequently percentages are used in daily life.
Te reo Māori vocabulary terms such as ōrau (percent), hautau (fraction), and hautanga ā-ira (decimal) could be introduced in this unit and used throughout other mathematical learning.
- Happy hundred board
- Metre ruler
- Rotating regions
- Several abacus
- 10 x 10 squared paper
- Decimal arrow cards
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
Session 1: Introductory session
Activity 1: Demonstrate and represent understanding of decimals with the use of different materials.
- Brainstorm on the group/class chart what students already know about decimals.
Record their ideas. (for example: “there’s a decimal point between whole numbers and parts”, “there are tenths, hundredths, thousandths”, “with decimal numbers you keep on dividing by 10 as you go to the right”, ‘deci is about ten’….).
- Make available to the students the following equipment:
10 x 10 squared paper, an abacus, rotating region, metre ruler, happy hundred board.
Have the students work in pairs. Each person should select a different piece of equipment.
Write several decimal fractions on the class chart (for example: 0.1, 0.01, 0.23, 0.5, 0.99, 0.001). Ask pairs of students to demonstrate and talk about what each of these looks like on their piece of equipment and agree. (note that 0.001 will be 1/10 of 1 square, bead, circle partition, centimetre and happy hundred face).
Listen to the language used and give feedback on what you hear.
- Ask students to return their equipment, and select a different item. Repeat the activity.
- As a class, discuss and record the common features of all the pieces of equipment (for example: they show 100 parts, each of which is 0.01 or one hundredth). Note that the metre ruler shows thousandths (mm) and squares on the grid are easier to partition into 0.001 than other representations on the equipment.
Activity 2: Explore the language of percentage and express decimal amounts as percentages
- Write the word percent on the class/group chart. Brainstorm together and record what this means to the students. Include contexts in which they hear ‘percent/percentage’ used (for example: shopping discounts, sports scores, political preferences, loading and display indicators on their computer/iPad).
- Write the percentage value beside the decimal numbers from Activity 1, Step 2 above. (10%, 1%, 23%, 50%, 99% and 0.1%) and have students show this on their chosen piece of equipment.
- Have students focus on the two number representations and record what they notice. For example: 0.1 is 1/10 and is 10/100 or 10%.
- Ask the student pairs to write their own definition of ‘percent’, and suggest why we use the word is ‘percent’ and the symbol %.
Ensure that the discussion includes these points:
A percentage is a way of expressing a fraction of 100, or another way of writing hundredths. Percent, from the Latin per centum literally means out of (per) one hundred (cent). The symbol % is made up of the / per sign and the two zeros (00) from the number 100.
Activity 3: Express decimal amounts as percentages
- Make a set of decimal arrow cards and paper available to each student pair.
Have them make a decimal number with their arrow cards. The number should be less than 1 and to two places only (eg. 0.15, 0.7, 0.05). Record it, make it on equipment and write this as a percentage.
- Have pairs share and discuss what they notice (when writing a decimal number as percent the decimal point ‘moves’ two places to the right). Demonstrate this with equipment, for example, 0.15: 0.1 is 1/10 or 10/100 and 0.05 is 5/100. Altogether this is 15/100 or 15%.
- Have pairs of students repeat this with three digit decimal numbers less than one.
Activity 4: Review and articulate the links between decimals and percentages
Conclude the session by having a student record the fractional representation of the decimal fractions and percentages recorded in Activity 1, Step 2, and Activity 2, Step 2 on the class chart: 10/100, 1/100, 23/100, 50/100, 99/100 and 1/1000 (or 0.1 of 1/100). Have the students read these to ensure they are saying the fraction correctly (hundredths and thousandths).
Record the students’ summary statements about the connections between decimal fraction, fractions and percentages.
Session 2
Make available to the students the percentage equipment from Activity 1, Step 2 above.
Activity 1: Introduction
Have these percentages recorded on the class chart. 25%, 50%, 75%, 10%, 20%.
Pass the Slavonic abacus around the class/group. As one student models the percentage on the abacus, have another record the fraction of the beads moved, in two ways.25% 25/100 1/4 50% 50/100 1/2 75% 75/100 3/4 10% 10/100 1/10 20% 20/100 1/5 - Ask what the students notice about the fractions (they are simplified to common fractions that we use everyday).
Activity 2: Calculate percentage amounts using knowledge of common fractions and their percentage equivalents.
- Pose the following problems for pairs of students to solve using common fractions. Students will need to be able to explain their solutions to the group. These problems could be displayed on a digital document, on which students’ solutions and calculations could then be recorded throughout the week. Adapt the contexts reflected in the problems to engage and interest your students.
Danny ate 10% of the 20 kiwifruit. How many did he eat?
Lily got 20% of the 40 votes. How many votes did she get?
Airini picked 50% of the 60 apples. How many did she pick?
Stevie mowed 25% of the 28 hectares of public lawns in the town. How many hectares did he mow?
- Have students pair share their solutions and discuss. Listen to their discussions and highlight any key points and their use of common fractions.
- Pose these problems and repeat Step 2 above.
Kiri ate 5% of the 20 kiwifruit. How many did she eat?
Andy got 15% of the 40 votes. How many votes did she get?
Mark picked 40% of the 60 apples. How many did he pick?
Jo mowed 65% of the 28 hectares of public lawns in the town. How many hectares did she mow?
- As a class discuss, record and model on the abacus strategies for finding 5%, (half of 10%) 15%, (10% + half of 10%), 40% (4 x 10% or 50% - 10%), 65% (6 x 10% + half of 10% or 50% + 10% + half of 10%).
- Make several abacus available to the students and have them write for classmates to solve (at least) 3 problems using personal contexts of interest and a percentage that you can work out using common fractions or combinations of these. They need to show and record the problem solutions. You could ask students to work in mixed groups, or could ask groups to write problems focused on finding different percentages.
Collect their written problems and explain that a group task sheet will be created from these to distribute at the next session.
Activity 3: Work out 100% from a given percentage.
Pose this problem:
How much is 100% if Manu eats 15 cherries and this is 5% of the bag full?
Have students discuss the solution in pairs. Share and demonstrate one way of thinking, using the abacus to look at the percentages and calculations then apply these to the problem.

5% x 2 = 10%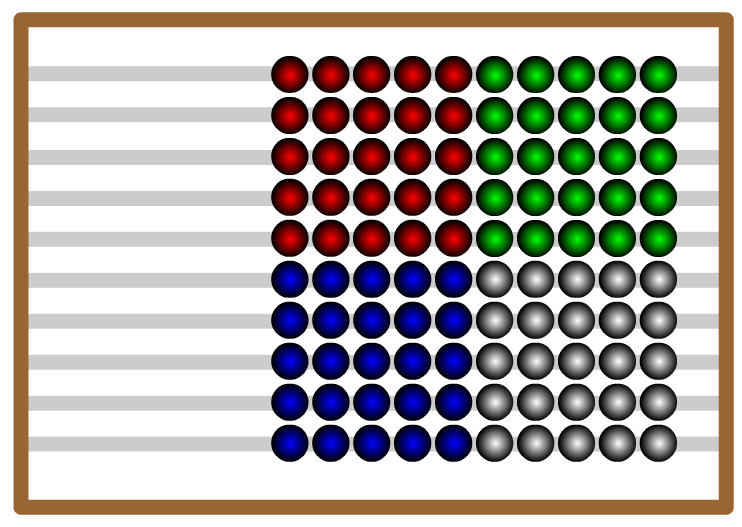
10 x 10 = 100%15 x 2 = 30 = 10% 30 x 10 = 300 = 100% Model twice more with a different number eg. 7 is 5%, 12 is 5%
- Distribute Copymaster 1.
Students can complete this on their own, or in pairs to practise working out 100% from a given percentage.. Have them show their thinking in the spare space provided. Some students may want to use equipment to explain their thinking as well.
- Pair share and discuss solutions.
- Record the students’ concluding remarks about using common fractions, particularly 1/10, and 10% to help to solve problems.
Before Session 3, compile selected student problems created in Activity 2, Step 4.
Session 3
Activity 1: Application of prior learning to student-generated percentage problems.
Review charted conclusions from Session 2.
Distribute student problems created in Session 2, Activity 2, Step 4.
Have students solve these on their own or in pairs. As a group, discuss solutions and have the student writers verify these.
Activity 2: Use knowledge of equivalent fractions to simplify ratios to common fractions and give a percentage percentage amount.
Review the charted list from Session 2, Activity 1, Step 1.
Ask a student to record beside each their decimal equivalent.25% 25/100 1/4 0.25 50% 50/100 1/2 (5/10) 0.5 75% 75/100 3/4 0.75 10% 10/100 1/10 0.1 20% 20/100 1/5 (2/10) 0.2 - Point out that, as they know, some percentage problems can be simply solved by simplifying a fraction to find a common fraction that is easy to change to a percentage.
- Pose these three percentage problems:
Tom shot 9 of the 36 goals that his team scored. What percentage was this?
Marni ate 4 of the 40 feijoas in the bowl. What percentage was this?
21 of the 28 votes were for Mele. What percentage of the votes was this?
Have students work in pairs to solve the problems and pair share their results.
Tom shot 9/36 = 1/4 = 25% of the goals.
Marni ate 4/40 = 1/10 = 10% of the feijoas.
Mele won 21/28 = 3/4 = 75% of the votes.
- Have students suggest other amounts that they could simplify to common fractions, or multiples of these, and percentages on the list. Record these. (eg. 12/16, 10/20, 4/8, 9/90, 3/30 etc.)
Activity 3: Explore and model 1/8 and 1/3 as decimals and as percentages.
- Pose these questions:
The sale said that the price had been reduced from $27 to $18. What percentage discount was this?
Nathan paid $8 for a small bag of mushrooms. $1 of this was GST. What percentage of the total price was the GST?
- Ask a different student to model and explain the answer to each, using the abacus. The discussion will result in the student partitioning 100 beads into thirds and eighths, resulting in the need to find a 1/3 of a bead and 1/2 of a bead respectively.
Have a student record on the class/group chart the percentages (33.33% and 12.5%) and write this as a decimal fraction (0.3333 and 0.125).
- Refer to the conclusions drawn about the relationship between decimals and percentages in Session 1, Activity 3.
- On the chart record the fraction 9/27 and simplify it to 1/3. Ask a student to explain 1/3. Elicit the language 1 divided by or shared into 3.
Perform a long division problem, 1 ÷ 3 showing the result of 0.3333.
0.3333 r
3) 1.0000
Have students also calculate 1 ÷ 3 on a calculator. Discuss this as a percentage.
Ask students to change 0.3333 into 33.33 on the calculator. Ask what they did and elicit ‘multiplied by 100.’
- Repeat this with 1/8 and show how 1/8 becomes a percentage.
Ask the students to suggest how this can be recorded and elicit: 1/8 x 100/1.
- Using this ‘procedure’ explore the calculations for known common fractions such as 1/2, 1/4, 3/4, 1/5, 2/3.
For example:
1/2 : 1 divided by 2 = 0.5 0.5 x 100 = 50%
1/4 : 1 divided by 4 = 0.25 0.25 x 100 = 25%
Activity 4: Convert an ‘awkward’ fraction into a decimal and show as a percentage.
Ask: Could this help us if a problem does not involve a common ratio or fraction? Pose this problem:
7 of the 49 people in the room voted against the idea. What percentage is this?
First ask students to estimate a percentage.
7/49 = 1/7 : 1/8 is 12.5% and 1/5 is 20% so it will be in between 12.5% and 20% but closer to12.5%
Look at this on the abacus.
? 1/5 1/7 1/8
Have students calculate the percentage, using both long division and a calculator.
(1 ÷ 7 = 0 .1428 0.1428 x 100 = 14.28 %
This is: 1/7 x 100/1 = 14.28%
Refer to the original problem and record the answer:
7 of the 49 people in the room voted against the idea. What percentage is this? 14.28 % or round to 14.3%
- Explore this problem in the same way:
Zoe scored 19 goals out of 29 shots. What was her percentage success rate?
(19/29 x 100/1 = 65.5%)
- Record several student suggestions for further problems to solve, involving more tricky ratios, but using interesting contexts of their own.
- Have the students solve these problems using the calculation.
Activity 5: Explain percentage calculations
Conclude this session by reviewing learning in today’s session.
(Elicit the observation that we can use common fractions to work out some percentages. If a fraction is tricky, we can work out its decimal value by dividing the numerator by the denominator and change the decimal to a percentage by multiplying by 100).
Session 4
Activity 1: Review approaches to percentage problems
- Begin this session by reviewing conclusions from Session 3.
- Pass an abacus around the group and have students model some common fractions/decimals/percentages, giving all three ‘names’.
- Ask the students to describe two ways for working out percentage from a given fraction/ratio. Record these:
1. Look for fractions we can simplify, to make equivalent fractions for which we know or can work out percentages.
2. Calculate by dividing the numerator by the denominator to find the decimal amount and multiplying this by 100.
Activity 2: Review approaches to percentage problems
Distribute the sets of cards from Copymaster 2 to each pair of students. Purpose: to practise deciding how best to solve percentage problems.
Have them sort these into the two piles indicated, giving the percentage solutions for the “common fractions they know” group as they do so.
Activity 3: Work out percentages by proportionally adjusting ratios that include factors of 10
- Tell the students that a third way to find percentages will now be explored.
Display the abacus and ask, what are factors of 100? (1, 2, 4, 5, 10, 20, 25, 50, 100)
Record the ideas shared on the class/group chart, and have students demonstrate their answers: 1 x 100, 2 x 50, 4 x 25, 5 x 20, 10 x 10 on the abacus.
- Pose the problem:
Tahu solved 7 of the 20 problems. What percentage is this?
Have students discuss in pairs the solution to the problem.
Ask a student to model this on the abacus.
Establish 20 is a factor of 100
5 x 20 = 100Model 7/20
(screen 80 beads)Model 7/20 five times 


Write 7/20 x 5/5 = 35/100.
Model this again on the abacus.
Have students articulate that the value hasn’t changed as both the denominator and the numerator are multiplied by 5 (and 5/5 =1).
Return to the problem:
Tahu solved 7 of the 20 problems. What percentage is this? 35%
- Explore and have students model on the abacus, these examples:
What percentage is:
14 out of 50? (14/50 x 2/2 = 28/100 = 28%)
17 out of 25? (17/25 x 4/4 = 68/100 = 68%)
3 out of 10? ( 3/10 x 10/10 = 30/100 = 30%)
13 out of 20? (13/20 x 5/5 = 65/100 = 65%)
- Have students work in pairs to discuss and solve the following set of problems, imaging the abacus.
What percentage is:
35 out of 50?
21 out of 25?
7 out of 10?
9 out of 20?
Confirm solutions by having a student model these on the abacus.
Activity 4: Work out percentages by proportionally adjusting ratios that include factors of 10
Distribute Copymaster 3 to practise deciding how best to solve percentage problems.
List three ways students have to solve percentage problems:
- Look for fractions they can simplify, to make equivalent fractions for which they know or can work out percentages.
- Calculate by dividing the numerator by the denominator to find the decimal amount and multiplying this by 100.
- Look for denominators that are factors of 100 and multiply both the numerator and denominator by the same number to give a fraction of 100.
Students can now revisit Copymaster 2 in Activity 2, Step 1 above, this time sorting the problems into three groups. Have them choose several from each group to solve, then write some of their own problems. This could be completed in pairs (tuakana-teina) or independently.
Activity 5: Work with and explain percentages greater than 100%.
- Write 200% on the chart. Have students discuss whether it is possible to exceed 100%.
Discuss some examples:
The temperature was predicted to reach 25oC. It reached 30oC.
This was 120% of the prediction. (1/5 higher than 100%, 30/25)
My goal was to save $100. I saved $130.
This was 130% of my goal. (130/100)
I figured the job would take me 15 minutes but it took half an hour.
This was 200% of the anticipated time. (double, 30/15)
The death toll was expected to be 80. Sadly the final toll was 200.
This was 250% of the expected toll. (2 1/2 times, 200/80)
- Ask students to suggest examples and record these.
Activity 6: Review approaches to percentage problems
Circulate Copymaster 4 to pairs or small groups of students.
Ask groups to decide whether each statement is right or wrong.
They should pair share and take turns to work through the examples and demonstrate and explain their rationale. Make equipment available.
Conclude the session by recording key ideas developed in the session.
Session 5
Activity 1: Calculate a percentage amount from a total amount.
- Pose the problem and make calculators available.
Steffi scored 23% of the 78 goals. How many goals did she score?
Ask student pairs to first record an estimate and then calculate a solution.
Give them time to work out how to do this.
- Discuss why the solution is 0.23 x 78 = 17.94, round to 18 (0.23 is 23 hundredths, so this is 23/100, or 23% of 78). So Steffi scored 18 goals.
- Have students offer (at least) three other similar problems from their own contexts. Record these. Have student pairs solve these, share and explain their solutions.
Activity 2: Estimate solutions to decimal and percentage problems and explain rationale.
- On the class chart write ‘estimation’. Ask students provide a definition of estimation and reasons for estimating.
- Have students explain in pairs how they would estimate the following:
9.5% of $165 (10% is $16.50 so 9.5% around $15.50)
14% of 360 (10% is 36, 5% is 18, so 15% is 36 + 18 = 54, so 14 percent is around 50)
26% of 164 (25% is 41 so 26% is around 43)
82% of 600 (80% is 4/5, 1/5 is 120, 4/5 is 480, so 82% is around 490)
Record student estimates.
Distribute calculators and ask students to check their estimates.
Discuss sensible rounding.
Record student calculations beside estimates and compare.
- Distribute the game Estimate Match (Copymaster 5) for 2 to 4 players.
Purpose: to further develop percentage estimation skills.
Some students can write new problems on the spare cards provided.
- Conclude the game then discuss the most difficult estimates, exploring reasons for this.
Activity 3: Understand and calculate percentage increase and decrease problems.
- Write ‘percentage increase/decrease’ on the class/group chart and circulate Copymaster 6. Have student pairs discuss and solve these problems involving percentage increases and decreases.
Have them pair share and explain their thinking.
These concepts can be modeled on the abacus, by the teacher or by students as necessary.
For example:
This is 100% of the beads.

This is 200% of the beads.
The beads have increased by 100%.
There has been an increase of 100%.
This is an increase to 200% (the original 100%, + 100%)


This is 300% of the beads.
The beads have increased by 200%.
There has been an increase of 200%.
This is an increase to 300% (the original 100%, + 200%)Pose additional problems.
The original price for the timber for the fence was $397.
Two years later the price had increased by 200%. How much will the fence timber cost now? Discuss.
What if the $397 price had been reduced by 100%?
This is 100% of the beads.This is what they look like if there is a decrease of 100%. Zero. - Because of the popularity of the style, the $30.00 price of the T-shirt was increased by 40%. Two weeks later it was reduced by 40%. Rick said, “The price is back to $29.00 again.” Is he right?
Have students discuss this and justify their Yes/No decision.
This can be readily modeled on the abacus.
For example:
Show 30 beads, add 12 beads (increase of 40% of 30 which is 12)
Show 42 beads
Show 42 beads and subtract 17 beads (decrease of 40% of 42 which is 16.8, round to 17)
Show 25 beads
No, Rick is not right.
Highlight that the percentage increase and decrease relate to different amounts.
- Return to Copymaster 6, looking carefully at the language of “to, by, of” and the amounts that the increase or decrease relate to.
Pose and try other examples parallel to those in Copymaster 6.
Activity 4: Work out an original price from a given percentage discount and discounted amount.
- You may want to pose and explore this final problem, although it is conceptually challenging:
You receive a 15% discount on your T-shirt and pay $24. What was the original price?
Ask how students might approach this problem.
Reword it this way:
If you received a 15% discount then you have paid 85% of the original price. How can you find the original price?
Students could investigate this using a calculator.
(Students may find 15% of 24 by calculating 24 x 0.15, and then add this on to 24. But this does not give the original price because the 15% calculated relates to the discounted price, not to the original price.)
Look at it this way:
The original price $? was multiplied by 0.85 to give the discount price.
Therefore, to find the original price, this process is reversed.
The discount price is divided by 0.85 to give the original $? price.
For example: $40 (original) x 0.85 = $34 (discounted price)
($40 has been discounted by 15% by multiplying 40 by 0.85)
Therefore to find the original price (in this case we know it is $40), the reverse must happen.
That is, $34 (discounted price) ÷ 0.85 = $40 (original price).
Therefore dividing 24 by 0.85 will give the original price= $28.24.
15% of 28.24 = 4.24.
$28.24 – $ 4.24 = $24 (the discounted price).
- Students could suggest a diagram for this to show what is happening.
Together, investigate some of the examples suggested by students , making sense of what is happening.
- Conclude this session by recording student reflections on what they have learned in working with percentages.
Dear parents and whānau,
We have been working with percentages in class. Ask your child to tell you about what they have been learning. They can teach you to play the game Estimate Match. A copy of the game is attached.
We trust that you find this both challenging and enjoyable.
