Wheeling and Dealing

Activity One

This activity is about divisibility: whether a number will divide evenly into another with no remainder. Knowledge of divisibility is very important at the advanced multiplicative stage because it allows students to identify common factors, which is the key to proportional reasoning. For example, to identify that 48/64 is equivalent to 3/4, a student must spot that both 48 and 64 are divisible by 2, 4, 8, and 16.
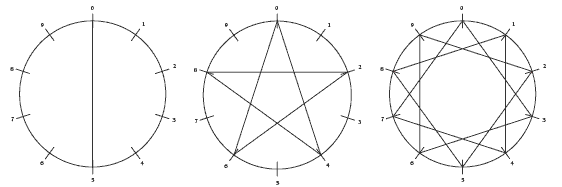
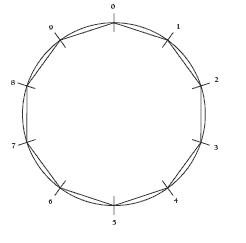
The students need to be aware of the connection between factors and multiples. Multiples are the answers to a given set of multiplication facts. For example, 4, 8, 12, 16, and so on are the multiples of 4. They are numbers that come up when you skip-count in fours from 0. Factors are numbers that multiply together to give a certain number. For example, 4 and 6 are factors of 24 because 4 x 6 = 24. The connection between factors and multiples is this: if 24 is a multiple of 4, then 4 must be one of its factors. Also, this means that 24 must be divisible by 4. Using a digit wheel to graph the ones digits of multiples produces interesting patterns and can, for some numbers, indicate criteria for being or not being in a set of multiples. For example, digit wheel patterns of the multiples of 5, 4, and 3 look like this:

The digit wheel pattern of multiples of 5 shows that for a number to be a multiple of 5, it must have either 0 or 5 as its ones digit. This is the divisibility test for 5. To be a multiple of 4, the number must have an even number as its ones digit. This is not the definitive rule for divisibility for 4 because there are some even numbers that are not multiples of 4, like 18 and 34. However, it does eliminate all the odd numbers from being multiples of 4. The digit wheel pattern for the multiples of 3 shows that the ones place gives no clue as to whether or not any number is divisible by 3. Every digit is visited on this wheel.
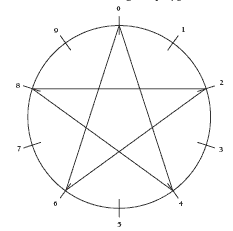
Some multiples form the same pattern on the digit wheel but visit the digits in reverse order. For example, the digit wheels of 1 and 9 both produce this pattern:

Multiples of 2 and 8, 3 and 7, and 4 and 6 also have similar digit wheel patterns. Note how these pairs of matching numbers add up to 10. Question 3b is set to see if the students can generalise that no matter how many tens, hundreds, and so on are added to the base multiple, the pattern in the ones digit will remain the same. For example, the pattern for multiples of 6 will be the same as that for the multiples of 16, 26, 186, 506, 7 546, and so on. That’s because multiplying tens, hundreds, and so on does not alter the ones digit. We need to look further than the ones digit
when testing for divisibility by all digits except 1, and 5.
Activity Two
This activity considers a test for divisibility by 3. The test is based on the fact that every 10 is divisible by 3 with 1 left over. Likewise, every hundred, thousand, ten thousand, and so on is also divisible by 3 with 1 left over.
Any whole number is made up of combinations of these powers of 10. For example, 795 is made up of 7 hundreds, 9 tens, and 5 ones. If 1 is taken from each ten and hundred, what is left will be divisible by 3. The only concern then is whether the collection of ones is divisible by 3. 795 has 7 + 9 + 5 = 21 extra ones. 21 is divisible by 3, so 795 must be divisible by 3.
The same principle can be used to test for divisibility by 9 because every ten, hundred, thousand, and so on is divisible by 9 with 1 left over. So for 795, the ones can be collected in the same way, but they must add to a number that is divisible by 9. 21 is not divisible by 9, so 795 is not divisible by 9.
Refer to pages 19–33 of Book 6: Teaching Multiplication and Division in the Numeracy Project series for lesson notes on teaching divisibility by 9 and 3.

Extension

The students can explore how the divisibility tests for 3 and 9 can be used to work out division answers and remainders. In the case of 795:
• Each 100 contains 33 threes with 1 left over, that is, 7 x 33 = 231 threes with a remainder of 7 ones.
• Each 10 contains 3 threes with 1 left over, that is, 9 x 3 = 27 threes with a remainder of 9 ones.
• The extra 7 + 9 + 5 = 21 ones make another 7 threes.
• This gives a total of 231 + 27 + 7 = 265 threes. So 795 ÷ 3 = 265.
By similar reasoning, 795 divided by 9 must be:
• 77 nines from the hundreds with 7 ones remaining
• 9 nines from the tens, with 9 ones remaining.
• From the 7 + 9 + 5 = 21 ones, another 2 nines can be made with 3 remaining.
• The total number of nines is 77 + 9 + 2 = 88, so 795 ÷ 9 = 88 r3.
Note that the answer to a given number divided by 3 is always 3 times larger than the same number divided by 9. In the case of 795, 265 = 88 1/3 x 3 (because the remainder 3 is 1/3 of 9).
The students can also investigate other divisibility rules, such as:
• If the last two digits of any whole number form a 2-digit number that is divisible by 4, then the number is divisible by 4. For example, 78 536 is divisible by 4 because 36 is divisible by 4. This results because every hundred, thousand, and so on is divisible by 4, for example, 100 ÷ 4 = 25.
• If a number is divisible by 2 (an even number) and it is also divisible by 3, then the number is divisible by 6. For example, 576 is divisible by 3 because 5 + 7 + 6 = 18. 576 is also even, so it must be divisible by 6, that is, 576 ÷ 6 = 96.
 

Answers to Activities

1. a. Practical activity. The pattern of the ones digits repeats as you carry on to higher
multiples of 4. The plotting line for the pattern visits only even digits, 0, 2, 4, 6, 8,
and forms the following star polygon.

b. No. 47, 95, and 783 are all odd numbers and therefore do not have 0, 2, 4, 6, or 8 as their ones digit.
2. a. A vertical line joining 0 and 5
b. If the ones digit is 0 or 5, the number is a multiple of 5.
3. a. Multiples of 3 or 7 or any numbers with a ones digit of 3 or 7
b. Yes. The ones digits would form the same pattern because the tens digits do not affect the pattern.
4. Practical activity

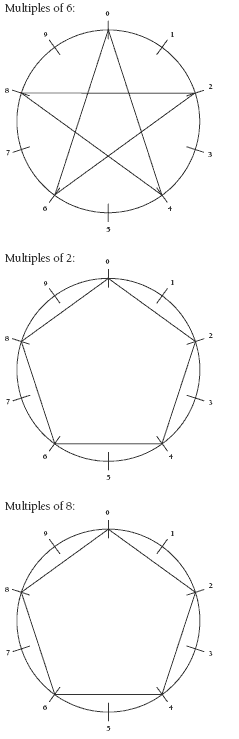
The multiples of 6 form a star like the multiples of 4.
The multiples of 2 and 8 form a pentagonal pattern. The only difference is the order in which the points are joined.
5. a. Same as multiples of 1
b. Decagon, like multiples of 9
The following diagram applies to a and b.

c. Pentagon, like multiples of 8. (See the diagram for the multiples of 8 at
question 4.)

Activity Two

1. a. 4 + 2 = 6, so 42 is divisible by 3.
b. 7 + 5 = 12, so 75 is divisible by 3.
c. 8 + 8 = 16. 16 is not divisible by 3, so 88 is not divisible by 3.
d. 10 + 2 = 12, so 102 is divisible by 3.
2. a. 2 + 7 + 3 = 12, so 273 is divisible by 3.
b. 4 + 1 + 4 = 9, so 414 is divisible by 3.
c. 5 + 2 + 3 = 10. 10 is not divisible by 3, so 523 is not divisible by 3.
d. 6 + 7 + 2 = 15, so 672 is divisible by 3.
e. 1 + 1 + 1 + 0 = 3, so 1 110 is divisible by 3.
f. 3 + 5 + 6 + 1 = 15, so 3 561 is divisible by 3.
3. Yes, because multiples of 9 will have digital sums of 9. (A digital sum is the sum of the digits.) For example, 81 has a digital sum of 8 + 1 = 9, and 567 has a digital sum of 5 + 6 + 7 = 18, 1 + 8 = 9.