On Top of the World

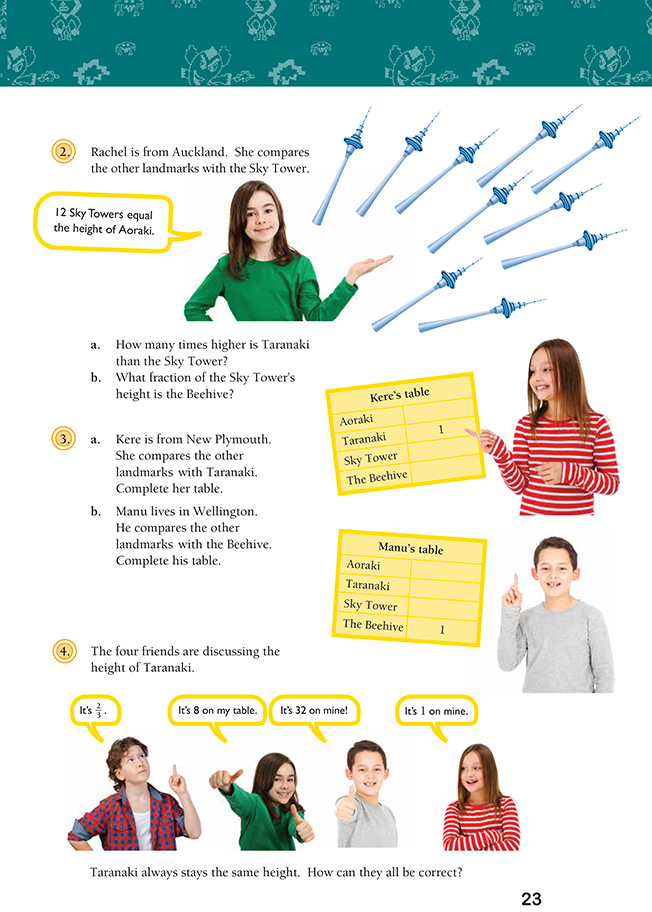
In this activity, students explore the idea that a fraction can be used to compare one thing with another without knowing the exact height of either. This helps to develop ideas of “openness” and reunitising, which are critical in algebra. The students discover that the same object can have a completely different fraction when it is compared with a series of different objects.
For this activity, the students need to be able to make comparisons in fractional terms, for example, 8 is 2/3 of 12 or 12 is 1 1/2 times bigger than 8. The diagram in the activity will help them do this. The students also need to recognise that numbers less than 1 (such as 2/3) and numbers greater than 1 (such as 5/4, 1 1/4, and 3/1 or 3) are all fractional numbers.
Set the scene with a guided teaching group by talking about local landmarks and asking the students what they think tourists would find interesting in your local area. Ask the students whether they have ever visited the landmarks in the diagram and, if so, what they were like.
Encourage the students to refer back to the diagram for each new question and establish which landmark is now defined as the “benchmark” (the landmark against which all others will be compared). Encourage them to predict whether the other landmarks will be described using a fractional number larger or smaller than 1 in each situation. (If the landmarks are being compared with Taranaki, the height of Aoraki will be a fractional number larger than 1 because it’s taller than Taranaki, but the Sky Tower will be a fractional number less than 1 because it’s shorter than Taranaki.)
Question 4 is a useful point for making formative assessment observations to determine whether the students can explain that fractions are comparative numbers and comment on the importance of one whole in this comparison. Another useful question to promote algebraic thinking is: Can a quarter ever be bigger than a half? (Yes. 1/4 of 40 is 10, and 1/2 of 6 is 3. But you can’t compare the physical sizes of quarters and halves unless they are both fractions of the same whole amount.)
For your information, the actual heights of the landmarks are: Aoraki: 3 754 metres,
Taranaki: 2 518 metres, Sky Tower: 328 metres, and the Beehive: 49 metres. These heights have been used very approximately in the student activity.

Answers to Activity

1. a. 1/12
b.1/48
2. a. 8
b.1/4
3. a.

3b.

4. They are all correct because the numbers are comparing the height of Taranaki with that of different landmarks. The other landmarks are all different heights, so the comparisons are different fractional numbers (32 and 8 are also fractional numbers: in this case, for Taranaki in comparison to the other landmarks, 32 as a fraction is and
8 is 8/12. A fractional number is a number used to compare a subset and its set or a part to the whole.)