This is a level 3 measurement activity from the Figure It Out theme series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (284 KB)
use multiplication to find areas of rectangles
A calculator (optional)
In this activity, the students will need to apply their knowledge of area and how to calculate the area of rectangular shapes. This may be the first time they have found area from a diagram drawn to scale. You should discuss why it is not possible to do a drawing of the actual park in the book and why it has to be represented by a diagram drawn to scale. In this case, the scale is 1 : 1 000 or 1 centimetre : 10 metres.
The students will have had previous experiences finding area by counting non-standard units and concrete units, such as 1 centimetre cubes and squared diagrams (or pieces of fudge, as on page 4). From this, you will need to check that they understand and can express in their own words that the area is found by “multiplying the measurement along the length by the measurement across the width” as they may have done with a multiplication array. Some visual models of 1 metre square
would also be helpful for imagining dimensions involved in the task. The students will have worked with 1 metre square in page 4 of Measurement, Figure It Out, Levels 2–3. The students will probably find it easier to begin by calculating the area of this year’s gala.
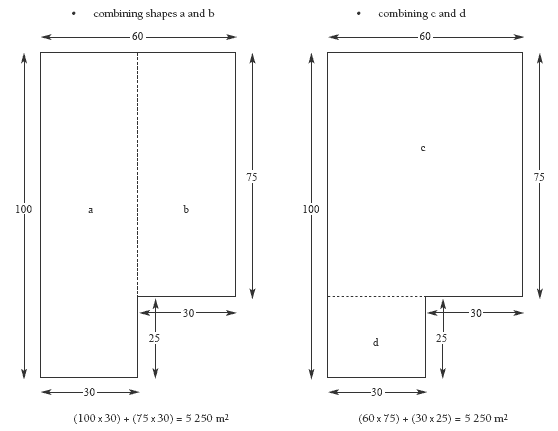
Encourage the students to use a problem solving approach to investigate different
ways of finding the area of last year’s gala.
This may include:
• taking the smaller rectangle away from the larger
During the activity, encourage the students to stop to discuss and share the strategies that the groups are using before they continue to work out other strategies. Students having difficulty with formal measurement could compare the two shapes using concrete materials and non-standard units.
Don’t forget to compare the measurements of the two diagrams to answer the original problem. As an extension, the students could attempt to draw an irregular shape with the same area as this year’s gala field.
Answers to Activity
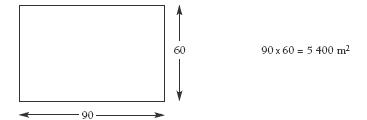
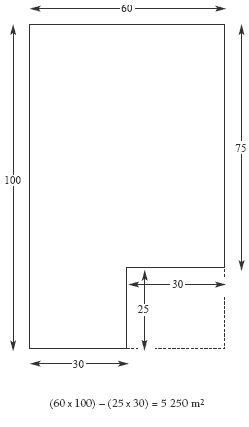
Yes. The total area of the park used for last year’s gala is (75 x 60) + (30 x 25) = 5 250 m2. The area available for this year’s gala is 90 x 60 = 5 400 m2.