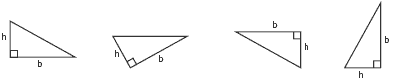Tempting Tangrams

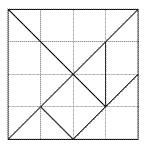
The tangram is a deceptively simple geometrical puzzle. The pieces are easy to make using card and scissors but can be combined in ways that challenge both students and adults. This activity focuses on the areas of the different pieces relative to each other and to the completed square.

When making the pieces in question 1, the students should use thin card so
that they can fold it cleanly. If they later want to make a more durable set, they
can draw a 4-by-4 grid of suitably sized squares on thicker card and then make
the pieces by joining the appropriate intersections, as in this diagram:

To answer questions 2 and 3, the students need to compare the area of each
piece with the area of the smallest right-angled triangle. They may need some
help with the idea that a triangle can represent a square unit. If this is the case,
you could get them to cut one of the small triangles in two and re-form the two
halves as a square. Area does not have a shape!
In question 4, the students need to give their answer in units (rather than length as measured by a ruler). They could work backwards from the area of the big square (16 square units) and use the fact that this area is found by squaring the length of the side, or they could make a square from one of the small triangles (as suggested above) and then use its side to measure the length of the long side of one of the big triangles. They should remember that, while area is expressed in square units, length is expressed in units that are not squared.
If your students have difficulty with questions 2-4, you can simplify the maths for them by getting them to make a tangram set using a grid, as shown in the above diagram. If they leave the grid lines in place, they can easily compare the size of each piece by counting the squares. Conversely, you can make the maths more challenging by naming the area of another piece (one of the large triangles, for example) as 1 square unit and then getting the students to express the area of all other pieces in terms of this unit. To do this, they will have to use fractions.
Question 5 is unlikely to be obvious or easy but creates a valuable teaching opportunity. The four pieces clearly do not have the same number of sides, the same shape, or the same area. The clue is the fact that these four pieces were cut from the same strip: the strip that was left when A, B, and C were removed. This
means that they have the same height. They also have the same base length.
When students see the word "base", they often think that this means the bottom (horizontal) line of a shape. In everyday thinking, this is true, but in geometry, when we rotate a shape, we don't change its essential features. These four triangles are congruent (identical in all respects) even though the side labelled b for "base" isn't always at the bottom:

The teaching points here are that:

•  "height" and "base" are nothing more than labels; we can call any side the base
•  the height and base always form a right angle with each other
•  sometimes, we need to draw a height line. This can be done at any convenient place:

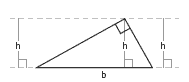
As an extension, you could challenge your class to think about what
happens to the areas of shapes when their heights change, as in this diagram:

Do the triangles still each have an area equal to half the rectangle?
Does the area of the parallelogram still equal the area of the rectangle?
If the height (the distance between the two parallel lines) is doubled, does the area of each shape also double? How could you show that this is, or is not, the case?
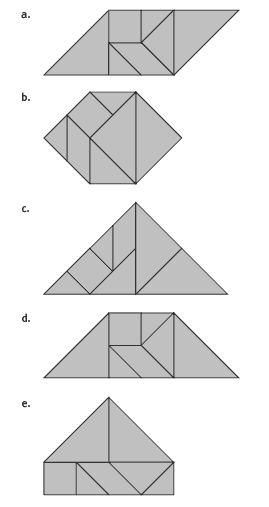
In question 6, the students use their tangram pieces to make geometrical shapes. Some will find this difficult at first, but they will get better as they understand the relative sizes of the pieces and develop some strategies. One useful strategy is to try and place the two large triangles first; in most cases there are only a few positions that they can occupy. The two small triangles can be left until the end; their positions will become obvious once the larger pieces are in place.
You may like to discuss with your students the fact that the parallelogram occupies a differently-shaped space when it has been flipped over (turned reverse side up). This is because it does not have reflective symmetry. Some series of tangram puzzles require the parallelogram to be flipped; others do not.
If your students get the "tangram bug", they could explore the subject using the Internet. There are websites that will give them plenty of challenges. Some of these feature interactive tangram sets. To find them, try "interactive tangram" in a search engine. 

Answers to activity

1. Practical activity
2. A and B: 4 square units; C, E, and G: 2 square units; D and F: 1 square unit
3. 16 square units
4. 4 units
5. They have the same base and height.
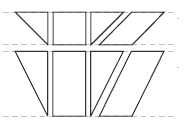
6. Practical activity. Here is one solution for each
shape. Other solutions are possible.