Team Schemes

This activity gives students opportunities to use a range of multiplicative strategies to solve practical problems involving multiplication and division.
For question 1, challenge students who simply add the numbers of students at each school to use a multiplicative method by asking How could you use Ms Kelly’s 7 x 30 statement to solve the problem in a different way?
Encourage the students to share their strategies for each problem in question 2 with the group and to talk about which was most efficient.
Possible part–whole multiplicative strategies to explore and compare include:
• using known facts and place value knowledge. For example, when solving 210 ÷ 3 = : if you know that 21 ÷ 3 = 7, you can use knowledge of place value to work out that 210 ÷ 3 = 70.
• using known facts and the distributive property. For 210 ÷ 6 = : if you know that
18 ÷ 6 = 3, you can use this to work out that 180 ÷ 6 = 30. There are still another 30 students to divide into 6-player teams: 30 ÷ 6 = 5. 30 + 5 = 35 teams.
• using partitioning. For 210 ÷ 4 = : you can partition 210 into 200 + 10 and then divide each part separately by 4. 200 ÷ 4 = 50, 10 ÷ 4 = 2 remainder 2, so 210 ÷ 4 = 52 remainder 2.
• making proportional adjustments. For 210 ÷ 5 = : 210 ÷ 5 = 420 ÷ 10 = 42.
• reversing and using multiplication. 210 ÷ 2 =  can be changed to 2 x  = 210.
 

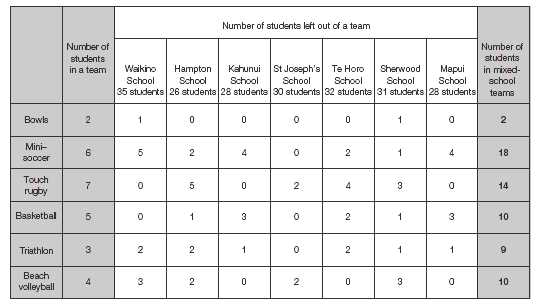
For question 3, encourage the students to design a table to help record all the information they need in a clear way. One possibility might be:

A key concept underpinning this problem is that of factors (a number that is multiplied by another number to create a product; if you divide a number by one of its factors, there will be no remainder. See Multiples and Factors, pages 16–17). Define the term “factor” together, then ask:

• There are 35 students at Waikino School. What are the factors of 35? (1, 5, 7, and 35)
• How does knowing about the factors of a number help you to know whether some students will need to play in mixed-school teams? (If the number of students in a team is a factor of the number of students at the school, there won’t be any remainders, and so no students from that school will need to be in mixed teams.)
• Which schools have fewer students who will need to go in to mixed teams? Why is this? (St Joseph’s School only has 4 students who need to go into mixed teams because they have 30 students and 30 has more factors than numbers such as 26 or 31.)
• A prime number only has two factors, itself and 1. Do any schools have a prime number roll? (Sherwood, with 31 students) How does this affect the numbers of students who will need to play in mixed teams?
(A school with a roll that is a prime number will have a lot more leftover students than a school such as St Joseph’s with its 30 students. For example, unless a team has 31 students in it, a school with 31 students will always have leftover students.)
If students have difficulty coming up with a fair way of scoring for question 4, direct their attention to
the speech bubble hint and ask questions such as:
• If you are in a winning team, how many points do you think each player in the team should get?
• What about if you draw? (You could get half the winning amount of points.)
• Would this system be equally fair to students who are in mixed teams?
• Would this system be fair to schools who have fewer students at the sports day?
• If each player in the mini-soccer team got, say, 5 points, how many points would the whole team have?(6 x 5 = 30 points) Would every sport be the same? (No, because it would depend on how many are in the team.)
Extend the problem by getting the students to design a syndicate sports extravaganza, using the numbers in your syndicate’s classes and coming up with their own team sports and team numbers (note that small teams are easier to work with for this problem):
• How many students are there altogether in our syndicate? Which multiplication fact would give you an estimate? (For example, 5 x 30 = 150)
• How many teams will be needed for each sport in your sports extravaganza?
• How many students will need to play twice so that everyone gets to be in a team?
• For each sport, how many players will need to be in mixed-class teams to make up numbers?
 

Answers to Activity

1. All of the schools have about 30 students, so Ms Kelly could work out how much more or less than 30 each school’s total is, add up all these positive and negative numbers, and then add or subtract the result from 210 (7 x 30).
(– 4 + 1 + 0 – 2 – 2 + 5 + 2 = 0, so there are exactly 210 students.)
2. 105 teams for bowls: 210 ÷ 2 = 105
35 teams for mini-soccer: 210 ÷ 6 = 35
30 teams for touch rugby: 210 ÷ 7 = 30
42 teams for basketball: 210 ÷ 5 = 42
70 teams for triathlon: 210 ÷ 3 = 70
53 teams for beach volleyball: 210 ÷ 4 = 52 1/2.
(2 students would probably have to play beach volleyball twice so that the 2 in the half team get a game.)

3.

This information is shown as a table below:

4. Answers will vary. For example, if each student on a winning team earns 2 points for their school, then the available points for each sport would be:
• 4 points for a win in bowls (because there are 2 players in a team)
• 12 points for a win in mini-soccer
• 14 points for a win in touch rugby
• 10 points for a win in basketball
• 6 points for a win in the triathlon
• 8 points for a win in beach volleyball.
This system is fair because each winning player earns points for their school.
This would also work very well for mixed teams, and the points could be halved for a draw.