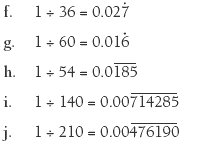Prime Time

Activities One to Three

These activities follow Primes and Emirps and build on the activities and investigations that the students have already done on those pages.
When the students are working through these activities, it is important that they understand the difference between “find the factors of”, “find the prime factors of”, and “factorise”.
In the first two instances, the answer will be a list of numbers, often (though not necessarily) expressed as a set and using set brackets. For example, the factors of 80 are {1, 2, 4, 5, 8, 10, 16, 20, 40, 80}. However, only two of these factors are primes, so the prime factors of 80 are {2, 5}.
In the third instance, the answer will be expressed as two or more numbers multiplied together. Often, this means “express as the product of its primes”, for example, 80 = 2 x 2 x 2 x 2 x 5. It can also mean “express as the product of two factors”, for example, 80 = 8 x 10.
In Activity One, the students need to find all the factors of 36, 56, and 84. They can do this without delving into primes, but if they begin by finding the prime factors, they will find it very easy to find all the factors of that number.
Before the students attempt the questions on the page, work with them on finding the factors of some other numbers. For example, 70 = 2 x 5 x 7. Obviously 1, 2, 5, 7, and 70 are factors of 70, but so also are 10, 14, and 35. These factors are found by pairing the primes, for example, 2 x 7. Students need to consider all possible pairings to be sure that they have found all possible factorisations.
Question 3 is a little more difficult in that the students need to consider combinations of three factors that multiply to give 84. As before, the first step is to establish that the prime factors of 84 are {2, 2, 3, 7}, so 84 = 2 x 2 x 3 x 7. The next step is to systematically look for combinations of 3 factors that will multiply to give 84:
• with 1 as the smallest factor: 1 x 1 x 84, 1 x 2 x 42, 1 x 3 x 28, 1 x 4 x 21, 1 x 6 x 14, 1 x 7 x 12
• with 2 as the smallest factor: 2 x 2 x 21, 2 x 3 x 14, 2 x 7 x 6 (no 1s allowed as these are considered in the first case above)
• with 3 as the smallest factor: 3 x 4 x 7 (no 1s or 2s allowed as these have been considered in the two cases above).
 

Prime factorisations make it easy to find common factors for two or more numbers. For example, 36 = 2 x 2 x 3 x 3 and 27 = 3 x 3 x 3. Their prime factors indicate that they have a common factor of 3 x 3 = 9. This means that 27/36 can be expressed as . (What we have done here is take out a common factor of 9, commonly called cancelling.)
In Activity Three, question 2, the students use this idea to solve problems involving rates. Expressed as a product of prime factors, 210 = 2 x 3 x 5 x 7. Similarly, 42 = 2 x 3 x 7. The prime factors 2, 3, and 7 are common to both, so the factor 2 x 3 x 7 must also be common to both. So 210 ÷ 42 = (2 x 3 x 5 x 7) ÷ (2 x 3 x 7), which equals 5.
Activity Four extends the ideas of divisibility to decimals that either terminate (end) or do not terminate. For any division 1 ÷ n =, the resulting decimal will terminate if n divides evenly into 10, 100, 1 000, and so on, because 1 is 10 tenths, 100 hundredths, 1 000 thousandths, and so on. Students who investigate this will find that this is only true if the prime factors of n are a combination of 2 and/or 5. For example, 1 ÷ 64 = 0.015625. This decimal terminates because
64 = 2 x 2 x 2 x 2 x 2 x 2 = 2⁶, so 64 divides evenly into one-million-millionths (another name for 1).
1 ÷ 36 = does not terminate because the prime factors of 36 are 2 x 2 x 3 x 3 and 9 does not divide evenly into any power of 10.
See pages 38–39, Book 7: Teaching Number Sense and Algebraic Thinking for more on these ideas.

Challenge

Students should generate a list of fractions in which the numerator is not 1 and then use a calculator to find which of them terminate. For ease of investigation, suggest that they limit their examples to fractions that have numbers no greater than 100 for both the numerator and denominator. Once they have found which of the fractions on their list terminate, they should factorise the numerators and denominators, where possible, and then look for common elements. They will find that as long as the only prime factors of both numerator and denominator are 2 and/or 5, the decimal will
terminate. If another prime is involved, the decimal will terminate only if that prime is a factor of both the numerator and the denominator. For example, 28/178 terminates because 28/178 = (2 x 2 x 7) / (5 x 5 x 7) and 7 is a factor of both the numerator and the denominator.

Answers to Activities

Activity One
1. The other possible 36-pot rectangular trays are:
1 by 36, 2 by 18, 3 by 12, and 6 by 6. However, 1 by 36 and 2 by 18 are unlikely in practice. (Note that the square 6 by 6 tray is also rectangular because it fits the definition of a rectangle: it has 4 right angles and opposite sides are equal.)
2. Other equal packets are: 1 pkt of 56, 2 pkts of 28, 4 pkts of 14, 8 pkts of 7, 14 pkts of 4, 28 pkts of 2, and 56 pkts of 1. However, some packets, such as 1 pkt of 56 and 56 pkts of 1, are unlikely in practice. (The factors of 56 are 1, 2, 4, 7, 8, 14, 28, and 56.)
3. The other possible boxes are: 1 x 1 x 84, 1 x 2 x 42, 1 x 4 x 21, 1 x 6 x 14, 1 x 3 x 28, 1 x 7 x 12, 2 x 14 x 3, 2 x 2 x 21, 3 x 4 x 7.
Activity Two
1. Paora’s method is different from the others because he begins by using 6 and 10 as his first factors. Holly and Amanda both start with 2 and 30 as factors. Holly then splits 30 as 2 x 15. Amanda splits 30 as 3 x 10.
2. Yes, because prime factors cannot be separated into two other factors. Other sets of factors for 60, for example, 2 x 2 x 15, include one or more factors that are not prime factors.
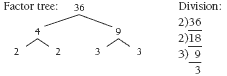
3. Strategies will vary. For example, you could use factor trees or division.

Prime factors are:
a. 36 = 2 x 2 x 3 x 3
b. 54 = 2 x 3 x 3 x 3
c. 72 = 2 x 2 x 2 x 3 x 3
d. 84 = 2 x 2 x 3 x 7
e. 140 = 2 x 2 x 5 x 7
f. 210 = 2 x 3 x 5 x 7.
Activity Three
1. a. Jane saw that there was an extra factor of 2 in the denominator, so the whole fraction is equivalent to 1/2.

2.

.
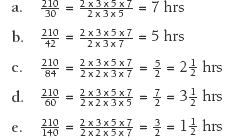
3. Yes. They can have 6 teams made up of 6 guides and 9 scouts. Using prime factors:
36 = 2 x (2 x 3) x 3 = 6 x 6
54 = 2 x 3 x (3 x 3) = 6 x 9
Activity Four
1. a. 1 ÷ 8 = 0.125
b. 1 ÷ 20 = 0.05
c. 1 ÷ 125 = 0.008
d. 1 ÷ 64 = 0.015625
e. 1 ÷ 100 = 0.01
So, yes, all these decimals terminate.

None of the divisions in this group terminate.
2. a. In each case where the decimals terminate, the divisor has no prime factors other than 2 and/or 5.
b. If the divisor has any prime number other than 2 or 5 as a factor, the decimal will not terminate.

Challenge

If a number other than 1 is involved in the division, the prime factors of the number being divided must be taken out of the divisor’s prime factors before the check
for factors other than 2 and 5 is done. For example, with 3 ÷ 120, the prime factors of 120 are 2 x 2 x 2 x 3 x 5. Taking out 3 as a factor leaves only 2 x 2 x 2 x 5, so the decimal will terminate. For 7 ÷ 22, the prime factors of 22 are 2 and 11. There is no 7 (the prime factor in the number being divided) to take out, but because 11 is a prime number other than 2 or 5, the decimal will not terminate.