Number Relations

Session 1

This session looks at aspects of relational thinking that relate to common addition strategies.

2. Write the equation 48 + 17 = 50 + 15 on the board and get students to think about how they know whether the equation is correct. They could also think about a contextual story for the equation, such as: “Tane has 48 pipis in his bucket and collects 17 more. Moana has 50 pipis in her bucket and collects 15 more. Who has the most pipis or do their buckets contain the same number?” You might model the situation with containers and place value-based materials, creating a collection for Tane (48 in the bucket and 17 outside it …).    
   Some ideas to discuss are:
   • Completing the addition on either side of the equal sign is one way to check the equality. 48 + 17 = 65 and 50 + 15 = 65. This strategy ‘closes’ the operations on both sides to provide a known amount on each side of equals.
   • 2 is added to 48 and 2 is taken away from 17 to get 50 + 15. Adding 2 and taking away 2 means the total doesn’t change so they must be equal. In this strategy the quantities on both sides of equal are treated separately to show how one side can be transformed into the quantity on the other.
   • Relationships between the numbers on both sides of equals are considered. 50 is 2 more than 48 but 15 is 2 less than 17 so the quantities should balance. Working with equality is relational thinking.
3. Ask students to show the equality using place value equipment.

4. Show students the following diagrams and get them to explain how they show the equality 48 + 17 = 50 + 15.    
   Operating on each side separately might be shown using the cup and bar models below. Working relationally might be shown using the empty number line model.    
        
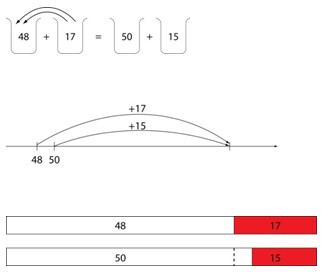
   Give similar equations for students to decide whether, or not, they are true, that the equality holds or does not hold. Get them also to show the equality (or inequality) using materials, or in some diagrammatic representation. Note that two equations below are incorrect.

   39 + 18 = 40 + 17	56 + 23 = 59 + 20	38 + 17 = 40 + 19
   67 + 24 = 57 + 34	236 + 38 = 238 + 40	52 + 227 = 50 + 229

5. Ask students to look at the equations and think about which side of the equal sign would be the easiest to work out and why. Use this discussion as a basis for the ‘tidy number’ strategy which could be used to solve the following equations:

   47 + 18

   34 + 69

   26 + 37

   438 + 48

   Look at the equations again. Can you decide if the equation is true without calculating the answers to both sides? How can you do that?

6. Discuss a couple of examples, one correct and one incorrect.    
   In 67 + 58 = 69 + 56, 69 is 2 more than 67 but 56 is 2 less than 58, so the equality must hold.    
   In 52 + 227 = 56 + 231, 56 is 4 more than 52 and 231 is 4 more than 227 so the right side is 4 more than the left, and the equation is incorrect.

7. The following additions require students to think about the additive relationship between the numbers on either side of the equal sign. It is important to get student to explain and discuss their strategies. Recognise that the greater the difficulty of calculation, the greater the likelihood that students will think relationally using equality. Provide place value materials and/or calculators to students who need that level of support.

   87 + 36 = 77 +	342 + 678 = + 478
   29 + 74 = 31 +	488 + 396 = 427 +

8. As students work, roam the room to look for the following:
   • Do they ‘close’ off one side of the equation by calculating the answer, then try to find the missing number by trial and error (a very inefficient method)? For example, 87 + 36 = 123 then find a number to add to 77 to get a sum of 123.
   • Having closed off one side do they use the inverse operation (subtraction) to find the missing number? For example, 342 + 678 = 1020, 1020 – 478 = 542.
   • Is relational thinking applied by maintaining equality? For example, 488 is 11 less than 499 so  is 11 more than 86, therefore  = 97.
9. Gather the class to discuss their strategies, raising the efficiency of those strategies as shown in the bullet points above.

10. To complete this session get students to think about what numbers could be put in the square and circle to make these equations true. Ask students to explain the relationship between the square number and the circle number and justify why the relationship must hold. Note that you are developing a solution set for each equation that can be generalised to a common relationship between the and  values.

    15 + = 14 +	+ 78 = + 68
    + 362 = 261 +	278 + = + 268

    In the example + 78 =  + 68, 78 is 10 more than 68 so the value of is always 10 less than the value of  . The generalisation can be developed by creating a table containing examples of values that work, such as:

    1	11
    10	20
    5	15
    100	110
    0	10
    17	27

Session 2

This session focusses on relational thinking and subtraction.

1. Ask students to think about why they don’t need to work out the subtractions on both sides of the equal sign to decide that this equation is true: 43 – 28 = 63 – 48. The key idea is that if you add the same amount to both numbers, the difference between them stays the same. However, students may not apply the fact the subtraction is not commutative, such as believe that 28 – 43 = 63 – 48. Use empty number lines to show whether the results of the calculations are likely to be the same.

2. Ask students to consider the truth of equations like the following, without working out the subtractions on either side of the equal sign:

   23 – 9 = 24 – 10	267 – 46 = 261 – 40	468 – 239 = 478 – 249
   63 – 38 = 61 – 40	2,548 – 1,376 = 2,648 – 1,476	456 – 78 – 450 – 70

   Students should also be able to explain their reasoning using diagrams and equipment. For example:

    

   

3. Introduce students to the term ‘equal addition’ as a strategy to make the subtraction easier to work out. This could also be ‘equal subtraction’, the main concept being that adding or subtracting the same amount to or from both of the numbers does not change the difference between them. Talk about the following two strategies used to make this subtraction easier to solve, and why it becomes easier:

    

4. Discuss how the strategy applies relational thinking by retaining the equality. Consolidate relational thinking with regard to subtraction by getting students to use the ‘equal addition’ or ‘equal subtraction’ strategy to solve the following problems.

   35 – 18 =

   64 – 39 =

   263 – 98 =

   632 – 148 =

5. Ask students to think about whether, or not, the ‘equal addition’ or ‘equal subtraction’ strategies could be used to solve addition problems. Use examples like:

   Is this equation true? Why, or why not?

   48 + 56 = 52 + 60

6. To complete this session, ask students to think about what numbers could be put in the square and circle to make these equations true. Ask students to explain the relationship between the square number and the circle number, and why the relationship occurs:

   65 – = 63 -

   – 32 = – 30

   – 18 = 74 –

Session 3

This session explores how relational thinking applies to multiplication.

1. Discuss why this multiplication equation is true, and what relationships exists between the numbers on the left of the equal sign and the right: 14 x 5 = 7 x 10
2. Re-arranging a 14 x 5 array to become 7 x 10 will help students to understand that nothing has been added or taken away to the array, so there will be the same number of items (Copymaster 1 is the pūkeko array):    
    
3. Relate the re-arrangement of the array with the more abstract equation representation such as:    
    

4. Give students some multiplication equations like the following for them to decide whether or not they are true, without working out either side of the equal sign:

   34 x 5 = 17 x 10	34 x 4 = 17 x 8	½ x 20 = 2 x 5
   20 x 4.5 = 10 x 9	68 x 2 = 39 x 3	1½ x 4 = 3 x 2

5. The following multiplications require students to think about the multiplicative relationship between the numbers on either side of the equal sign. It is important to get students to explain and discuss their strategies. Note that multi-digit multiplication is difficult to model physically so use easier examples at first where rearranging arrays can be used to represent the quantities on both sides of the equal sign.

   18 x 4 = x 8	124 x 48 = x 24
   60 x 15 = x 45	72 x = 36 x 150

6. To complete this session get students to think about what numbers could be put in the square and circle to make these equations true. Ask students to explain the relationship between possible values for the square number and the circle number, and why the relationship occurs. Use easier examples at first if students find these examples to difficult, such as 4 x = x 8. Develop a table of values first, if needed, to establish cases of the relationship.

   56 x = 28 x	x 7 = x 21
   66 x = x 22	x 15 = x 5
   15 + = 14 +	+ 78 = + 68
   + 362 = 261 +	278 + = + 268

Session 4

In this final session students are challenged to come up with their own ‘relational thinking’ division problems. They should be able to demonstrate and explain the correctness of their equations using materials and equation diagrams.

Measurement is a good context for showing how relational thinking applies to division problems. For example, dividing 24 litres of juice into 6 litre buckets will give you the same number of buckets as dividing 12 litres of juice in to 3 litre buckets:

This equality can be written as 24 ÷ 6 = 12 ÷ 3

Equal sharing is the other form of division and behaves in the same manner.

For example, sharing 24 litres equally among 6 people gives the same amount as sharing 12 litres equally among 3 people. The shares are both 4 litres per person.

This equality can also be written as 24 ÷ 6 = 12 ÷ 3

Make a collection of students’ equations. A nice way to provide problems for other students is to mask one number in the equation and ask a classmate to work out the hidden number.

For example, the original equation might be 48 ÷ 6 = 16 ÷ 2 and changed to 48 ÷ 6 = 16 ÷ □.