Making Money

The main focus of this activity is finding percentages and applying these in a practical context. Although some questions involve adding and subtracting money amounts, students will need to be at or beyond the advanced multiplicative stage of the Number Framework and learning to apply their multiplicative strategies to percentage problems.
In question 1, the percentage involved is 50 percent (%). This is easy to calculate because 50% is equivalent to half. Although the students should be able to use mental strategies to answer these questions, you could use this page to teach them how to use the percentage button on a calculator. To do this, they enter the manufacturing cost, press the multiply button, then 5 and 0 , then the percentage button. There are various ways that the students could use a calculator without a percentage button: they could enter the manufacturing cost and then multiply by 50 and divide by 100; divide the manufacturing cost by 2 to get a half (because 50% is a half); or multiply the manufacturing cost by 0.5 (which is also 50% or a half).
Question 2 can be done by addition: for each item, the cost to the clothing shop (the wholesale price) equals the manufacturing cost plus the manufacturer’s 50% profit.
To answer question 3, the students need to refer back to their answers for question 2. They can use the same strategy or calculation as they did for question 1, but they need to add the 50% in each case to the price paid by the clothing shop.
If the students are using calculators for questions 2 and 3, they can calculate the price that the retailer pays for the sweatshirt by doing two calculations:
1. Find 50% of the manufacturing cost
2. Add this 50% amount to the manufacturing cost.
Discuss with the students a quicker way to do this. They are adding half or 50% of the manufacturing cost to get the cost to the retailer, so the cost to the retailer is 11/2 times the manufacturing cost.This cost can be quickly calculated in one calculation: the manufacturing cost x 1.5 (which is 11/2) or times 150%. Students who use an efficient calculation like this show that they have the number sense to understand what they are doing when they add a certain percentage.
A mental strategy for question 4a is to calculate 1/10 of the customer cost (1/10 of $57.38 is $5.738), then double that to get 2/10 or 20% ($11.476 ≈ $11.48). Remind the students to round to the nearest cent at the end of their calculations to minimise inaccuracies.
The students may notice that the 20% discount is more than half the shop’s original profit. Encourage them to understand that a smaller percentage of a larger amount can be more than a larger percentage of a smaller amount.
A systematic way for the students to keep track of their calculations for this activity is to record the information in a table.

Question 4b i involves subtracting the original cost price of the items from their sale price (after the 20% discount) to find the shop’s sale profit on each type of sweatshirt. The students then multiply this amount to take into account the total number of individual items sold (5 three buttons, 2 short sleeves, and 1 basic style) and add the products together to find the shop’s total profit for the morning.
Question 4b ii involves looking back at the original non-sale profit for the three types of sweatshirts and subtracting the total sale profit found at 4b i from the total original or pre-sale profit. During the discussion in 4c, encourage the students to justify their reasoning with examples and to consider what profit margin a business would need to cover wages, electricity, rent, and so on and whether it’s acceptable in some circumstances to sell products below cost in order to reduce losses. (Or should a garment be left on the shelf in the hope it will sell eventually?)

Answers to Activity

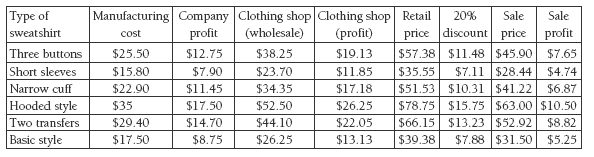
1. i. $12.75
ii. $7.90
iii. $11.45
iv. $17.50
v. $14.70
vi. $8.75
2. i. $38.25
ii. $23.70
iii. $34.35
iv. $52.50
v. $44.10
vi. $26.25
3. i. $57.38
ii. $35.55
iii. $51.53
iv. $78.75
v. $66.15
vi. $39.38
4. a. i. $45.90
ii. $28.44
iii. $41.22
iv. $63.00
v. $52.92
vi. $31.50
b. i. $52.98. ($317.88 sale price – $264.90 shop cost)
ii. $79.50. ($132.48 – $52.98)
c. Discussion will vary.