Animal Antics

In this activity, students solve problems that involve proportional relationships, using equivalent ratios.
The students are likely to find it very hard to know where to begin with question 1. The reason is that there are no obvious units to work with. But once they discover (or are shown) a way of dealing with this, they should have little difficulty comparing the relative strengths of the teams in each case. You may like to begin by letting your students spend some time in groups trying to find a way forward and then get them to report back on the problems they have or their successes. Alternatively, you may prefer to give them some scaffolding before they move into groups.
The simplest approach is to use either box diagrams or materials. (Visually, these amount to the same thing.) Materials could be strips of card that the students cut and label themselves. The strips need to be cut to fit the information in the two introductory illustrations. The yaks will be the shortest strips because they have the least pulling power. It doesn’t matter what actual length the students choose for the yaks, but they need to cut and label three strips, all the same length. They then need to cut another strip that is exactly the length of three yak strips end to end. If they fold
this strip in half and cut it on the fold, they will have two rhino strips. They can use all these strips to model the second set of information in the top panel:

They should then cut a new strip that has the length of 1 rhino strip and 3 yak strips joined end to end. This new strip should be labelled Elephant. The students can now use their strips to model the first set of information in the top panel.

It is very important that they understand that the length of the strip represents the strength of the animal: the longer the strip, the greater the pulling power.
By cutting additional strips for extra animals as needed, the students should now be able to use them to model each of the situations in question 1 and to solve the problems:
Question 1a:

Question 1b:

Question 1c:

Using the strips, the students should find it easy to make up and answer their own tug-of-war questions involving any combinations of the three animals.
As a further activity, you could challenge your students to work out the relative strengths of the three animals as a ratio. To do this, they will need to use a notional “unit of strength”. If they have trouble with this, suggest that they assign 2 units of strength to a yak. The elephant:rhino:yak ratio in its simplest form is 9:3:2. The box diagram illustrates this fact:

Question 2a requires the students to make proportional adjustments: they know how many bananas and apples are needed for each chimpanzee or monkey, so how many are needed for  chimpanzees and  monkeys? In question 2b, the students have to work in reverse. This is not too difficult for part i. In this case, it is clear that the number of animals involved must be very small, so trial and improvement should quickly find the right combination. The students might note that it takes 4 bananas and 5 apples to feed a monkey and a chimpanzee. 8 bananas and 10 apples is twice
that, so there must be 2 of each animal.
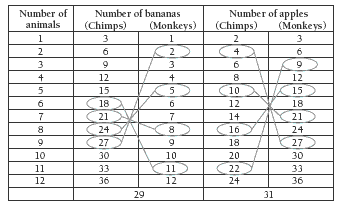
The students will probably find question 2b ii more difficult because there appear to be so many possible combinations of chimpanzees and monkeys to consider. One method is to use the “one of each animal” formula to get close to the desired numbers, then adjust. 4 bananas and 5 apples feed 1 monkey and 1 chimpanzee, so 6 monkeys and 6 chimpanzees would need 24 bananas and 30 apples. This total is close to 29 bananas and 31 apples. Adjusting the 6-chimpanzee-and-6-
monkey formula gives:

The alternative to trial and improvement is to find a way of systematically sifting the possibilities. Here is a suggested way of doing this using a table:

Once the numbers have been entered in the table, the students can use a pencil to circle combinations in the Bananas columns that add up to 29 and combinations of numbers in the Apples columns that add up to 31, as shown above. They should then list these combinations in another table, but with the focus on numbers of animals, not number of pieces of fruit as in the first table. There aren’t many combinations that add up to 29 and 31, and it should be immediately clear that there is only one combination of animals that exists for both types of fruit:

This kind of strategy works well in many different situations where we need to find one combination from a range of many possible combinations. Once the table has been drawn up, the students will quickly see that they can discard a lot of combinations for reasons such as “The sum is odd, so I only need to check combinations of even + odd.”
For questions 3a and 3b, 2 salad rolls + 2 drinks = $12, and 3 salad rolls + 1 drink = $14. The students need to approach this logically and intuitively. For example:
1. If 2 salad rolls and 2 drinks cost $12, 1 roll and 1 drink cost $6.
2. 3 rolls and 1 drink cost $14, so the 2 extra rolls cost 14 – 6 = $8, or $4 for 1 roll.
3. Given that 1 roll and 1 drink cost $6, if 1 roll costs $4, the drink costs $2.
The students can use this information to create the generalisation for calculating the cost of lunch in question 3c: number of drinks x $2 + number of rolls x $4 = cost.
In question 3d, the students could calculate the cost of lunch as 3 x $4 rolls + 3 x $2 drinks = $18, so the amount spent on muffins is 28.50 – 18 = $10.50 for 3 muffins. 10.50 ÷ 3 = $3.50 for each muffin. Alternatively, the students could start with 1 roll + 1 muffin + 1 drink = 1/3 x $28.50 and then use their answers to questions 3a and 3b to work out the cost of 1 muffin.

Answers to Activity

1. a. The elephant should win. 2 rhinoceros = 3 yaks; 1 elephant = 3 yaks + 1 rhinoceros; therefore the elephant is a whole rhinoceros stronger.
b. The 5 yaks should win. 3 rhinoceros would equal 4 yaks (and half a yak isn’t possible).
c. 1 elephant + 3 yaks should win. 4 rhinoceros = 6 yaks, and 1 elephant + 3 yaks = 6 yaks + 1 rhinoceros. So the left side is stronger by 1 rhinoceros.
2. a. i. (30 + 5) bananas and (20 + 15) apples = 35 bananas and 35 apples
ii. (45 + 20) bananas and (30 + 60) apples = 65 bananas and 90 apples
b. i. 2 chimpanzees and 2 monkeys. ([6 + 2] bananas and [4 + 6] apples)
ii. 8 chimpanzees and 5 monkeys. ([24 + 5] bananas and [16 + 15] apples)
c. A possible short cut for bananas is:
3 x number of chimpanzees + 1 x number of monkeys.
A possible short cut for apples is: 2 x number of chimpanzees + 3 x number of monkeys.
3. a. $2
b. $4
c. A possible short cut is: Cost = the number of salad rolls x $4 + the number of
drinks x $2.
d. $3.50. ($28.50 – $12 – $6 = $10.50. $10.50 ÷ 3 = $3.50)