- rautaki tatau;
- rautaki tāpiripiri;
- rautaki whakarea;
- rautaki pānga riterite māmā.
- whakaahua i roto hinengaro ngā rautaki hei whiriwhiri i te hautau o tētahi tauoti mēnā he tauoti te otinga;
- whiriwhiri i te hautau o tētahi tauoti (mēnā he tauoti te otinga) me te whai wāhi mai o ngā hautau nui ake i te kotahi.
E tino hono ana tēnei kōwae ako ki te Mahere Tau o Aotearoa (tirohia te kaupapa o Te Poutama Tau i te pae tukutuku o www.nzmaths.co.nz).
E whakaatu ana te wāhanga rautaki o te mahere tau i ngā momo rautaki ka whakamahia e ngā ākonga ki te whakaoti paheko.
E hāngai ana te mahi o tēnei kōwae ako ki te ākonga e piki ana mai i te Kaupae 7 ki te Kaupae 8 o te Mahere Tau.
I te Kaupae 7, e mōhio ana te ākonga ki te whakamahi i ētahi rautaki maha ki te whakarea tauoti.
I te Kaupae 8, e ako ana te ākonga ki te whakamahi i ētahi rautaki maha ki te whakarea hautau, tau ā-ira hoki.
|
Tāhei Hautau
|
Fraction Bar
|
|
rauemi matihiko
|
digital resources
|
|
mahi wehe kē
|
work independently
|
|
pāwhiri
|
click (the computer mouse)
|
|
pūtohu
|
button (on computer screen)
|
Kei tēnei wāhi i te ipurangi te rārangi mai o ngā rauemi matihiko katoa kua tuhia ki te reo Māori: Akoranga Matihiko
Ko ētahi o ngā rauemi matihiko (ngā mea o nzmaths) e wātea ana ki te katoa, mā te pāwhiri noa i te pūtohu. Ko ētahi atu o ngā rauemi matihiko (ngā mea o The Le@rning Federation), me rēhita kē tō kura, kātahi koe ka uru atu ai.
Koia nei te wāhi noho o te rauemi matihiko te Tāhei Hautau, e hāngai ana ki tēnei kōwae ako: http://www2.nzmaths.co.nz/maori/LO/taheihautau/index.html.
He Hononga ki Rauemi Kē
Tirohia te Pukapuka Tuawhitu o Te Poutama Tau.
Ka Mahi Tahi te Kaiako me tētahi Rōpū ākonga ki te Whakamahi i te Tāhei Hautau (ngā hautau mai i te 0 ki te 1)
- Huakina te Tāhei Hautau, ka whakamārama ai i tōna kaupapa ki te whakaatu i ētahi rautaki hei whiriwhiri i te hautau o tētahi tau.
- Pāwhiria te pūtohu e hāngai ana ki ngā hautau mai i te 0 ki te 1.
- Whakawhitiwhiti kōrero mō te whārangi tuatahi o te Tāhei Hautau, kia tino mārama ai ngā ākonga ki ēnei āhuatanga:
- Ko tā te tāhei he tohu i tētahi tau. E kimihia ana tētahi hautanga o taua tau.
- Ko tā te rārangi he tohu i te hautau o taua tau e kimihia ana.
I tēnei tauira, e whiriwhiria ana te 3/4 o te 28. E tohu ana te tāhei i te 28, ko te rārangi e tohu ana i te 3/4.
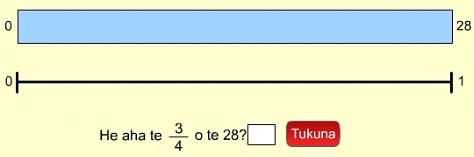
- I tēnei tauira, ka whakamahia te Tāhei Hautau hei āwhina i a koe ki te whiriwhiri i te 3/4 o te 28. Mēnā e mōhio ana koe ki te otinga me tuhi noa ki te pouaka. Ki te kore, ka whakamahia te Tāhei Hautau.
- Titiro ki te rārangi. Ko te 0 ki te pito mau?, ko te 1 ki te pito matau. Nō reira ki hea te 3/4? E Kiri, māu e pāwhiri te wāhi tika mō te 3/4.
- He nui ake, he iti iho rānei i te haurua? Kei waenganui pū i te haurua me te tahi.
- Ki te kore koe e mōhio ki hea te 3/4, me pāwhiri te pūtohu nei (whakaaturia ngā hauwhā). Koirā hei āwhina i a koe ki te kimi mai i te wāhi tika mō te 3/4.
- E Heta, pāwhiria te 1/4 i te rārangi. Tuhia te hautau 1/4 ki ngā pouaka e hāngai ana.
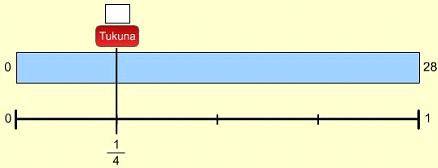
- Me pēhea te whiriwhiri i te 1/4 o te 28?
- Wehea te 28 ki te 4, ka 7. (28 ÷ 4 = 7)
- E hia ngā 4 kei roto i te 28? E 7. (4 x ? = 28)
- Hauruatia te 28, ka 14. Hauruatia te 14 ka 7. Koirā te 1/4.
- Tuhia te 7 ki te pouaka e hāngai ana i te tāhei.
- Ka taea hoki te whakaatu i te 1/2 (te 2/4 rānei) ki te rārangi mēnā e hiahiatia ana hei āwhina i a koe.
- Me pēhea te whiriwhiri ināianei i te 3/4 o te 28?
- Ko te 7 te 1/4 o te 28, nō reira whakareatia te 7 ki te 3, ko te 3/4 tērā o te 28. Arā ko te 21.
- Tāpirihia te 7 ki te 7, ka 14, Ko te haurua tērā. Tāpirihia tētahi anō 7, ka 21. Ko te 3/4 tērā.
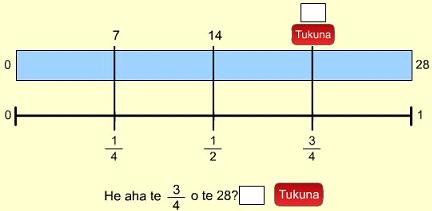
- Tuhia te 21 ki te wāhi e tika ana i te tāhei.
- Kei te kaiako te whiriwhiri mēnā ka mahi tahi i ētahi atu rapanga kia tino taunga ngā ākonga ki te whakamahi i te Tāhei Hautau, ka tukuna rānei ngā ākonga ki te mahi wehe kē.
- Ko te mea matua, kia mārama ngā ākonga ki te whakamahi i te hautahi (te 1/4) ki te whiriwhiri i te hautahi-kore (te 3/4) o tētahi tau. Hei tauira, 3/4 of 28 = 3 x 1/4 o te 28.
- Hoatu he rapanga hei whiriwhiri mā ngā ākonga. Kia taunga rā anō rātou ki te whakamahi i te Tāhei Hautau, kātahi ka tono i a rātou ki te whakaoti rapanga i rō hinengaro (e pai tonu ana te whakamahi i te pepa me te pene hei āwhina). Tonoa ngā ākonga ki te whakamārama i ā rātou mahi.
Ka Mahi Tahi te Kaiako me tētahi Rōpū ākonga ki te Whakamahi i te Tāhei Hautau (ngā hautau mai i te 0 ki te 2)
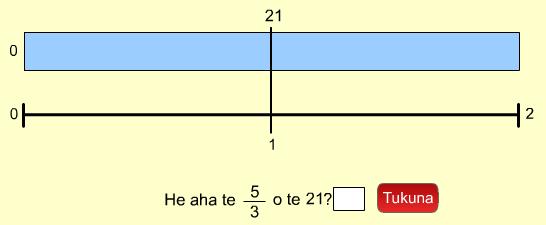
- Pāwhiria te pūtohu e hāngai ana ki ngā hautau mai i te 0 ki te 2. Ko te nuinga o ngā hautau i konei, kei waenganui i te 1 me te 2. Aratakina ngā ākonga ki te whakaoti i te rapanga ka puta mai. Ko te tauira rapanga e whai ake nei, ko te whiriwhiri i te 5/3 o te 21.
- Whakawhitiwhiti kōrero mō te whārangi o te Tāhei Hautau ka puta:
- Ko te 21 kei waenganui pū i te Tāhei. He aha ai? E noho hāngai ana te 21 ki te 1 i te rārangi hautau.
- He aha i puta ai te 1 me te 2 ki te rārangi hautau? Nā te mea e kimihia ana te 5/3 o te 21. Kei waenganui te 5/3 i te 1 me te 2.
- Ki hea tau ai te 5/3 i te rārangi tau? Ki waenganui i te 1 me te 2. He nui ake i te 11/2.
- Ki te kore koe e mōhio ki hea te 5/3, me pāwhiri te pūtohu nei (whakaaturia ngā hautoru). Koirā hei āwhina i a koe ki te kimi i te wāhi tika mō te 5/3.
- Pāwhiria te wāhi i te rārangi tau e hāngai ana ki te 1/3. Tuhia te 1/3 ki ngā pouaka.
- Whakawhitiwhiti kōrero mō te whakatau i te wāhi e hāngai ana ki te 5/3.
- Ki konei te 1/3, nō reira ki hea te 5/3? Tatauria kia 5 ngā hautoru.
- He nui ake, he iti iho rānei te 5/3 i te 1? He nui ake.
- E hia ngā hautoru kei roto i te 1? E 3.
- E hia atu anō kia 5/3? E 2 atu anō ngā hautoru.
- He aha te 1/3 o te 21? Tuhia ki te pouaka.
- Nō reira he aha te 5/3 o te 21?
- Kei te kaiako te whiriwhiri mēnā ka mahi tahi i ētahi atu rapanga kia tino taunga ngā ākonga ki te whakamahi i te Tāhei Hautau, ka tukuna rānei ngā ākonga ki te mahi wehe kē.
Te Whakarea i tētahi Tau ki tētahi Hautau
Ko tā te Tāhei Hautau he whakatauira i tētahi o ngā rautaki hei whiriwhiri i te hautanga o tētahi tauoti. Ko te whāinga matua kia kaua rātou e whakawhirinaki ki te Tāhei Hautau, ki te rautaki kotahi rānei ki te whakaoti i ngā rapanga pēnei i te 5/3 o te 21. E tika ana kia mārama te ākonga ki ngā rautaki maha me ngā āhuatanga tātai o te whakarea.
He uaua te whakamahi i te rautaki e whakaaturia ana i te Tāhei Hautau hei whakaoti i te 5/3 o te 14. He uaua te whiriwhiri i te 1/3 o te 14, me te whakarea i te otinga ki te 5, nā te mea ka whai wāhi mai he hautanga atu anō:
1/3 o te 14 = 4 2/3
5 x 4 2/3 = 20 10/3
= 23 1/3
He māmā ake tētahi atu rautaki pēnei i tēnei:
5/3 x 14 = 1/3 x 5 x 14
= 1/3 x 70
= 23 1/3
Tirohia te Pukapuka 7 o Te Poutama Tau, kei reira ētahi ngohe e hāngai ana ki ngā rautaki nei.
Ka Mahi Takitahi, Takirua rānei ngā ākonga
Ka whakaputaina e te Tāhei Hautau ngā rapanga hei whakaoti mā ngā ākonga. Nō reira, kia taunga rātou ki te whakamahi i te Tāhei Hautau, e pai ana kia tukuna rātou kia mahi takitahi takirua rānei.
Kia oti ētahi rapanga, tonoa rātou ki te whakamahi i te pepa me te pene ki te whakaatu i te rautaki hei whiriwhiri i te hautanga o tētahi tauoti.
Kātahi ka tonoa rātou ki te whakaoti rapanga pēnei i rō hinengaro.