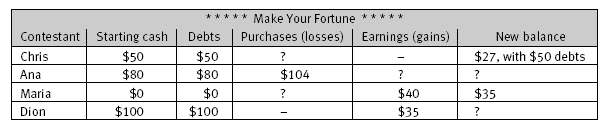This is a level 4 number link activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (251 KB)
add and subtract integers
Toy Money (optional)
FIO, Link, Number, Book Four, Money Matters, page 21
A classmate
This activity gives students experience in sorting through relevant information and thinking out how to use it in a way that makes sense in terms of the questions being asked. Working through information systematically and using logic and reasoning will help the students to keep track and write appropriate equations. It may be beneficial to solve question 1 together co-operatively as a class or group, with you guiding the discussion.
A useful starting point would be to collate all the relevant information about Chris. We know that Chris:
• has $50
• owes $50
• buys a CD
• has $27 left with two bills to pay.
Ask the students: “How do we calculate the cost of the CD?” ($50 – $27).For question 4, the students will need to recognise that Chris will be disqualified because, even if he used his $27 to repay debt, he would still owe $23.
In question 2, we know that Dion:
• has $100
• owes $100
• makes $35.
His balance could be found by either ($135 – $100) or ($100 – $65) or ($100 – $100 + $35).
Also in question 2, we know that Maria:
• has $0
• owes $0
• earns $40
• buys three guitar strings
• finishes with $35.
So her guitar strings cost $40 – $35.
Ana in question 3:
• has $80
• owes $80
• pays $104 for radio advertisements
• has $55 left. (She has $20 more than Dion or Maria.)
So she must have made $104 + $55 = $159 from her garage sale.
Another way to work through this activity is to summarise each person’s story so that it can be traced in a table. In the second column, put the amount each contestant had to begin with and in the third, put the debts they have to work with. The fourth and fifth columns can be for purchases (losses) or earnings (gains) and the sixth column for the new balance.
The students will still need to read each person’s situation carefully and summarise it with appropriate equations.
Answers to Activity
1. a. $23. ($50 – $27)
b. Yes. (Chris has $27, but he still owes $50, so he is not debt-free.)
2. $5. (Dion earns $35 by working for the restaurant. Maria finishes with $35, the same as Dion, so her guitar strings cost $5.)
3. $159. (Ana finishes with $20 more than Dion and Maria, which takes her to $55. Her radio advertisements cost $104. $104 + $55 = $159)
4. Answers will vary. (Note that contestants are disqualified if they are not debt-free at this point.)