Getting Round to It

Activity

In this activity, students discover the differences between a circle and an ellipse and how these two shapes are related. Ask students what they know about circles and ellipses and how they might go about drawing them. (For example, an egg is an elliptical shape. Planets follow an elliptical path.)
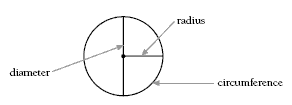
The activity provides opportunities to use mathematical language. Students need to understand that  to make their circle as round as possible, the person standing in the centre needs to make sure that their end of the rope remains in the same place so that every point on the circle (the circumference) is the same distance from the centre. The distance from the centre of the circle to the circumference is called the radius. The line segment that passes through the centre and goes from one side of the circle
to the other is called the diameter.

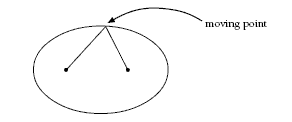
An ellipse is the path formed by a moving point so that the sum of the distances from two fixed points to the moving point is always the same.

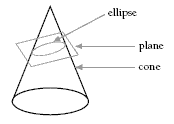
An ellipse can be described as a regular oval. An ellipse is also produced when a cone is cut obliquely by a plane.
Discuss with students which parts of the ellipse are regular or equal, for example, the two halves of an ellipse, divided either vertically or horizontally.

Answers to Activity

1. a. Practical activity
b. The rope works in the same way as the
compass by ensuring that there is a fixed
distance from the centre of the circle. (This
distance is called the radius.)
2. Practical activity
3. a. The ellipse becomes closer in shape to a circle.
b. As the 2 people move closer together, the 2 lines begin to behave more like the
radius of a circle. Eventually the 2 points would become 1 point, and this would be the centre of the circle.