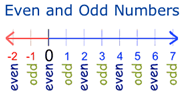
The purpose of this unit is to explore a pattern that is central to our number system: odd and even numbers.
- Identify even and odd numbers.
- Independently investigate, recognise and report on the patterns and characteristics of even numbers and of odd numbers.
- State generalisations about the addition and subtraction of even numbers and of odd numbers.
- Investigate and recognise the results of adding and subtracting combinations of odd and even numbers.
- Apply generalisations about odd and even number patterns to problem solving situations.
The purpose of these lessons is to enable students to recognise odd and even numbers and their characteristics, to generalise their behaviours when added or subtracted, and to be able to consistently apply these generalisations with problem solving contexts.
Our number system is made up of odd and even numbers. This is a fundamental pattern structure that requires focused exploration by students.
In many early primary classrooms, students are provided with opportunities to recognise odd and even numbers and to count aloud using these distinct number sets. However, investigation into their unique behaviours is not always given priority.
The members of each set of numbers behave in a particular way, as do the members of both sets when they work together in each of the four number operations.
The activities suggested in this series of lessons can form the basis of independent practice tasks. It is also assumed that throughout the school day, all class members, students and teacher alike, will look for and take opportunities to apply learning included in this unit of work.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- repeating activities as required
- extending examples to larger numbers
- providing extended opportunities for students to repeat and explore tasks as individuals, with partners, and alongside the teacher
- providing modelling, explicit teaching, and targeted scaffolding at all stages of the unit
- developing the use of diagrams and expressions alongside the use of materials and digital representations
- encouraging students to work in pairs or small groups. Providing opportunities for students to work in a range of flexible groupings can encourage greater peer learning, scaffolding, and extension.
The activities in this unit can be adapted to increase their interest to students, by adding contexts that are familiar to them. Whilst the focus of the learning is on number properties, the various activities could be carried out with whatever equipment motivates your students. Encourage your students to consider a range of real-life contexts in which they encounter odd and even numbers.
Te reo Māori kupu such as taukehe (odd number), taurua (even number) and tatau (count) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share relevant vocabulary from their home language.
- Packets of packaged items (eg. muesli bars, raisins, cans of drink, etc.)
- Number Strips
- Coloured see-through plastic counters
- Multilink or unifix plastic cubes
- Hundreds boards
- Pencils and paper
- Copymaster 1
- Copymaster 2
- Odd and Even Patience (Copymaster 3)
Session 1 (Exploring even numbers)
Activity 1
- Make number strips and coloured see–through counters available to students. Have them work in pairs, sharing a number strip, and counters of one colour only. Using a single colour enables greater focus on the concept being developed.
- Place a selection of pre-packaged food or drink, which have an even number of individual content items, in front of the students. Have students handle and check the number of items in each package, and then place a counter on that number on their number strip. The result will be that their number strip has several even numbers each covered with a see-through counter.
- On the class chart or modelling book, record these numbers and have the students tell you what they notice. Elicit from the students, or tell them, that these are all even numbers. Have the students suggest reasons why commercial packaging mostly works in this way and record their ideas. For example: ‘They’re neater that way’, ‘There’s no extra ones sticking out’, ‘The rows are equal’, ‘They’re in pairs’, etc. Agree that these are all reasons why the identified numbers are known as even numbers.
- Have students now place counters of the same colour on each even number on their number strip. Have one student read even numbers to twenty aloud, removing the counters as they do so. Then have the other student begin at twenty and count back in even numbers, replacing the counters as they do so. Repeat if necessary. Recognise the pattern that they make: the counters are on every second number.
Activity 2
- Make multilink or unifix plastic cubes available to students. Group the students in a way you feel is appropriate to the needs of the class. Have the students make a cube model of each of the even numbers to at least 10, depending on the number of cubes available. Provide time for them to discuss and record what they notice.

Record students' ideas on the class chart or modelling book. For example: ‘you keep on adding 2’, ‘it’s +2 each time’, ‘they go in pairs’, ‘they match and have partners’, ‘they’re called even because there’s none left over’, ‘it’s kind of fair’ etc.). Recognise that this is a pattern that grows by +2 each time.
- Have students, on their own paper or think-board, draw a picture of the even numbers. For each number, have them record the number of pairs there are.
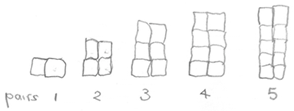
Provide time for paired discussions and recording of ideas. This should focus on what is noticed about the even numbers drawn and the numbers of pairs,
- Have students share their ideas and once again record them on the class chart. Elicit the important language of ‘times two’, ‘double’ and ‘half’. For example: ‘The number of pairs is half the even number of cubes,’ ‘The number is 2 times or double the number of pairs’, ‘It’s like the two times tables’, ‘When you say 4 times 2 it’s like saying 4 pairs’.
- Pose the question: “How can we find out if this is true for all even numbers?” Accept all responses and discuss.
- Make hundreds boards and counters available. Have students place counters on even numbers greater than 20.
- Record, using the class chart, the patterns students identify, and their descriptions of these numbers: ‘they all end in 0, 2, 4, 6, or 8’.
- Give students time to investigate the generalisations made in Step 4 above, ‘prove’ these with at least three numbers greater than 20. For example: 48 is 24 pairs, 48 is double 24, 24 is half 48, 24 x 2 = 48
- Have students describe to their partner or to the class, an even number they have chosen. Encourage them to demonstrate their discovery, using the language of ‘times two’, ‘double’ and ‘half’.
Activity 3
- Refer to the packages in Activity 1, Step 1 that have an even number of component items. List other content numbers on the class chart. For example: one pack with: 6 pottles of yoghurt, 10 ice blocks, 8 cans of drink, 2 packets of soup, 12 packets of raisins, etc.
- Pose this investigation:
Sam Shoppers says: “No matter which of these packages I put into my shopping trolley, I will always have an even total number of items.”
- Have students, working with a partner, use the equipment (cubes and hundreds boards) to show whether they agree or disagree with Sam Shopper (i.e. that when you add even numbers you always get an even total number). Emphasise that students should be able to explain their position to the class and show this with materials. Provide time for the completion of this challenge, including demonstrating their rationale using cubes.
- Conclude this session by writing on the class chart the generalisation: When even numbers are added together the sum is always an even number.
Activity 4
- Distribute a copy of Copymaster 1 to each student. Have students individually complete the problems, then discuss their ideas with a partner.
- Discuss what has been noticed and, on the class chart, record the agreed generalisations for subtraction and zero.
- When an even number is subtracted from an even number, the result is always an even number.
- Zero is an even number. (It ‘fits into’ the pattern of even numbers and when zero is added or subtracted from an even number, the result is an even number.)
Activity 5
- Conclude the session by having students create their own poster, poem or story about even numbers. Consider having the student choose some even numbers and give them personalities in their writing (anthropomorphism). For example: ‘Even Steven likes to...'
- Challenge the students to check the packaging of items at home or in the supermarket to see if all packages are made up of even numbers. Ask to find and write down the names of any products they find with an odd number of content items.
Session 2 (Exploring odd numbers)
Activity 1
- Begin with having students share their posters, poems or stories about even numbers.
- Place packages from Session 1 in front of the students. Ask if anyone has found packaging that has an odd number of items. Point out many packages (bags) of produce, (for example carrots, tomatoes) contain an odd number of items. Discuss possible reasons. (eg. the items are not always a uniform size and therefore it may take an odd number of them to make up the advertised weight.)
- Record on the class chart or modelling book, student predictions of things that they think they will discover about odd numbers. Accept all suggestions, including possible misconceptions such as odd number + odd number = odd number.
- Make number strips and see-through plastic and counters of two colours available to students. Have students work individually or in pairs, to cover the even numbers, saying the numbers aloud as they do so. Have them ‘fill in the spaces’, with another colour, saying the numbers aloud as they do so. Identify these as the odd numbers. Provide time for them to discuss what they notice about the way they are placed on the number strip.
- Make multilink or unifix plastic cubes available. Have the students make (or draw) the odd numbers with cubes, noticing how many they add each time to make the next odd number.
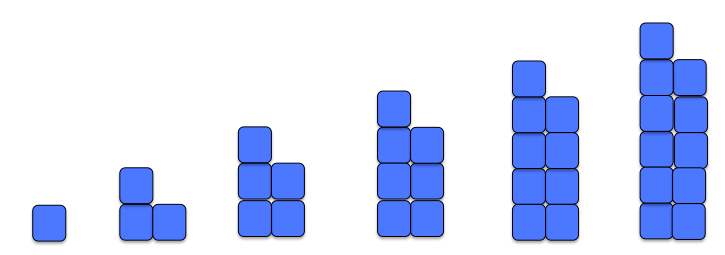
- Have students share what they notice and record these on the class chart. Elicit the important language and key ideas of : ‘There’s always one sticking out or left over,’ “Most are in pairs, then there’s an odd one without a partner.’ ‘They’re called odd numbers because they’re not all in tidy pairs,’ ‘It’s not just double or times two any more’, ‘It’s like a double of something plus one’.
- Highlight that a feature of even numbers is that it is a plus two (+2) pattern. If it has not already been noted, ask students to describe the growing pattern of odd numbers. Agree (and generalise) that the pattern of odd numbers grows by an even number, +2. Have students confirm this on the number strip and with their cubes.
Activity 2
- Make hundreds boards and counters available. Have students place counters on odd numbers greater than 20.
- Record on the class chart the patterns they see and what they notice about these numbers: ‘they all end in 1 3, 5, 7, or 9. Note the similarities and differences in the physical patterns made with the counters on the board, for odd and even numbers (i.e. columns of odd numbers alternate with columns of even numbers.)
- Ask if there are any other kinds of whole numbers other than odd and even numbers. Record responses, including odd and even negative integers if this discussion arises.
- Have students suggest some odd numbers of produce (eg. 11 carrots, 7 tomatoes.) Write on the class chart. Have student pairs investigate addition and subtraction of these odd numbers, recording their equations as they do so. Explain that they will be reporting their findings to the class and will need to explain and show the results of their investigation using equipment or a diagram.
- After student explanations, record on the class chart the generalisations:
When one odd number is added to another odd number the sum is an even number.
When an odd number of odd numbers are added together, the result is an odd number.
When an even number of odd numbers are added, the result is an even number.
When one odd number is subtracted from an odd number the result is an even number.
Ensure that students demonstrate each of these generalisations with materials. For example. (‘s’ is the student notation for ‘spare’ cube.)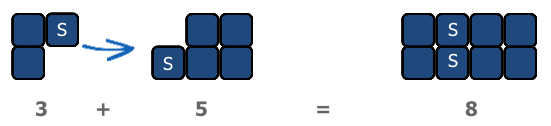
- Conclude the session by having students draw their own diagram to show the addition and subtraction of pairs of odd numbers, with an accompanying explanation.
Session 3 (Exploring combinations of odd and even numbers)
Activity 1
- In the class modelling book/chart draw an empty Venn diagram with the headings odd numbers and even numbers. Have students interpret the task and suggest what they might do. Confirm the following:
- Students should write what they have found out about each set of numbers in the correct place. If something is true about both sets, it belongs in the segment that is the intersection of both sets (for example: when you add two of these numbers, the sum is an even number).
- Have students share and discuss their Venn diagrams and generalisations. Reach clear agreement.
Activity 2
Make multilink or unifix plastic cubes available. Write a model of a recording chart in the class modelling book. For example:
Our odd and even number investigation Problem Example/investigation Result even + even = ? 2 + 4 = 6 
even even - even = ? 8 - 4 = 4
diagram/picture worth promotingeven Have student pairs follow your model and create their own recording chart. They should use this to investigate and record the addition and subtraction of odd and even numbers.
- Have student pairs share their investigation findings with another pair of students. Have each pair write a tick, on the other pair's chart, beside the statements that they agree with.
Have students discuss these as a class, and complete a class summary of generalisations which include:
Even ± even = even Odd ± odd = even Even ± odd = odd Odd ± even = odd
Activity 3
- Ensure that students can see a copy of the generalisations of the ‘behaviour’ of odd and even numbers when number operations are applied.
Distribute a copy of Copymaster 2 to each student. Have them individually complete the problems, then discuss their ideas with a partner. Emphasise that they must use the words ‘odd’ and ‘even’ in each of their explanations.
- As students finish have them play in pairs, Odd and Even Patience. (Copymaster 3).
- Conclude with a discussion of student learning about the patterns of odd and even numbers. Ask students to articulate how this information will be useful as they estimate and solve number problems in the future.
Dear families and whānau,
The numbers that we use in our number system are either odd or even. (Did you know that 0 is an even number?)
In class we have been exploring the patterns of odd and even numbers, including finding generalisations for what happens when they are added and subtracted. Like this:
| Even ± even = even | Odd ± odd = even |
| Even ± odd = odd | Odd ± even = odd |
Please take time to discuss this with your child and to enjoy playing the game, Odd and Even Patience. You’ll need a pack of playing cards. The instructions are attached.
Thank you.