Olympic training
This problem solving activity has an algebra focus.

Rose and Ron are training for the Olympic Games.
They start off swimming from different ends of the pool and when they reach the opposite end they immediately turn and keep swimming.
When they meet the second time, Ron is swimming to the right end.
At that moment the ratio of their distance from the left end to the right end is 3:2.
What is the ratio of Ron’s speed to Rose’s speed?
- Form and solve linear equations.
- Use ratios.
- Devise and use problem solving strategies to explore situations mathematically (draw a diagram).
To solve this problem, students are likely to first draw a diagram. From the diagram, they may more readily be able to express the situation using an equation. This will enable them to find a solution. To be able to generate and use an equation in this way, is an important mathematical skill to develop.
The Problem
Rose and Ron are training for the Olympic Games. They start off swimming from different ends of the pool and when they reach the opposite end they immediately turn and keep swimming.
When they meet the second time, Ron is swimming to the right end. At that moment the ratio of their distance from the left end to the right end is 3:2. What is the ratio of Ron’s speed to Rose’s speed?
Teaching Sequence
- Interest the students in the problem with a brief discussion of well-known swimmers.
- Pose the problem to the class and ask for ideas about how the problem might be solved.
- As the students work on the problem in pairs, check that they are recording their work so that they can communicate their solution to others.
Ask questions that focus on their understanding of ratios and the strategy they are using.
What does a 3:2 ratio look like in terms of their position in the pool?
How did you figure that out? - Depending on their experience, the students may need some support with the forming of a linear equation. Ask questions that encourage them to consider the different pieces of information given in the problem, and how these can be expressed in an equation:
How far has Rose swum when they met?
How can you record that?
How far has Ron swum when they met?
How can you record that? - Share solutions.
Extension
This time, the ratio of the distance from the left side of the pool when they met the second time, to the distance from the right side of the pool when they met the first time is 6:5. What is the ratio of Ron’s speed to Rose’s speed this time?
Solution
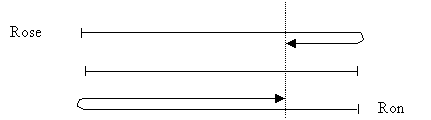
Let the length of the pool be L. When they meet Ron has travelled L + 3/5L and Rose has travelled L + 2/5L. So the ratio of their speeds is ![]()
Solution to the Extension
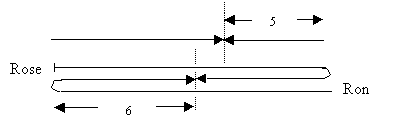
When they first meet Ron has swum 5 units and together Rose and Ron have swum the length of the pool, L units. When Rose and Ron next meet, together they have swum 3L units. But for every length that they swim together, Ron swims 5 units. So at their second meeting, Ron has swum 3 x 5 = 15 units.
But when they meet the second time, Ron has also swum L + 6 units. So 15 = L + 6, so L = 9.
Now we know that when Ron and Rose first meet them, Ron has swum 5 units and Rose L – 5, which is 9 – 5 = 4. So the ratio of Ron’s speed to Rose's speed is 5:4.