In this activity, the students investigate number patterns generated from triangular numbers. They will need to use problem-solving strategies, such as drawing diagrams and making tables, to identify and continue the number patterns.
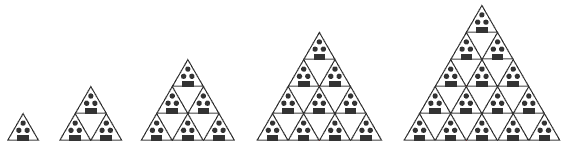
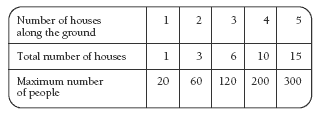
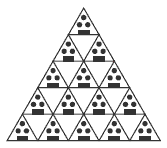
Encourage the students to look for patterns in the number of houses. For example, without the antigravity device, the number of houses are triangular numbers. Question 1 asks the students to use triangles or draw a diagram. Ensure the students read the question properly and say how many more houses could be built. They could then add to their diagram the number of houses along the ground, the total number of houses, and the maximum number of people. For example:

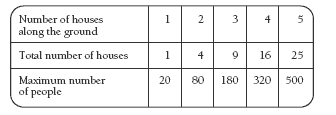
The students will need to make up a different table to complete the anti-gravity problems in questions 3 and 4.

From this table, the students may see a pattern developing where the total number of houses is the number of houses along the bottom multiplied by itself (that is, t = n x n), and the maximum number of people is the total number of houses multiplied by 20 (that is, p = t x 20). Using this reasoning, they would be able to calculate the maximum number of people for any number of houses along the ground.
Extension activities could involve looking at different “islands”, each with different bases. For example, an island called Gamma has room for only six A-frame houses along the ground.
As an extension to question 3, you could ask the students this question: “Anti-gravity houses cost half the price of normal houses. Each normal house costs 100 Delta dollars. What are all the houses worth altogether?”

Answers to Activity

1. 7, to make 15 in total

2. No, there will only be enough housing for 300 people.
3. 25
4. a. No, there will only be enough housing for 200 people.
b. Yes, there will be enough housing for 320 people.