In this activity, students learn that they need to think carefully before deciding that change is proportional and whether proportional change is direct or inverse.
There are two main approaches that you could take when introducing the activity to your students.
• Put them into problem-solving groups and set them to work on it. Each of the scenarios is simple enough to generate discussion. It will be interesting to see how soon groups realise that proportional reasoning may not be appropriate in all cases.
• Discuss the activity with your students before they begin, alerting them to the learning outcome at the bottom of the page and emphasising the importance of using common sense before applying proportional reasoning to a problem.
The key question in each case is “Is it possible to solve this problem using proportion?”
In question 1, the ingredients in the large and small quantities of muesli are directly proportional: for less muesli, you need less of the ingredients. Students may find it helps to use a ratio table:

Alternatively, they may reason “We need to know how many 160s there are in 800. Since 10 x 160 = 1 600 and 1 600 is double 800, it must be that 5 x 160 = 800. So we need to divide all the amounts by 5.”
Get the students to report back with their strategies. Restate the explanations to help others understand them, and record them on the board.
There is no answer to question 2. If the students are unable to see this, or are uncertain, they could use plastic beans, marbles, or similar materials to act out the scenario a number of times, recording their findings. (The logistics will be easier if they divide all numbers by 10.) They will see that each time they withdraw the required number of beans, the result is different.
You may like to discuss the fact that proportional reasoning can nevertheless be used in a case like this to work out the kinds of outcomes that are more likely or less likely. In other words, introduce probability as a mathematical tool that can be used to analyse the scenario. Given, for example, that there are twice as many blacks as yellows, it is probable that a blindfolded person who removes some beans from the jar will end up with more blacks than yellows. This trend would certainly become obvious if the experiment were conducted many times. It can be confirmed mathematically by looking at the ratios of the numbers of beans of the different colours:

Students should not confuse what is probable with what will happen. If a blindfolded person took 50 jellybeans from the jar as described, they would probably get some of each colour, more blacks than any other colour, and fewer whites. But then again … all 50 could be black!
The “catch” in question 3 is that the relationship between consumption and duration is inverse: the big fish eats three times as much as the little fish, so the packet of food will last the big fish just one third as many days.
Question 4 encourages students to think algebraically as they try to find a rule to connect the number of eagles and the number of trapeziums. Suggest that they make a table connecting eagles and trapeziums:

Ask “What patterns can you see in the numbers?” They should see that each time an eagle is added, the number of trapeziums increases by 3. Ask “Why does the number needed go up by 3 trapeziums when there are 4 in each eagle?” They should see that each eagle added to the first shares a trapezium.

This information can now go into a short cut: either (20 x 3) + 1 = 61 for twenty eagles, or (19 x 3) + 4 = 61. Encourage your students to verbalise a generalisation for this pattern and record it algebraically, for example: to find the number of trapeziums, multiply the number of eagles by 3 and add 1. Algebraically, this can be written as t = (e x 3) + 1 (where t stands for the number of trapeziums and e for the number of eagles).
Most students will have had some experience of running and should recognise that no runner can sustain a sprint speed for a long distance. This means that question 5 cannot be solved using proportional reasoning.
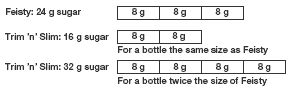
Question 6 is not difficult, but like a lot of questions involving proportional reasoning, it may be hard for students to work out where to begin. A strip diagram can be a useful tool for visualising the problem and seeing the relationship between the various bits of information:

Question 7 is the most straightforward part of this activity: the cost is directly proportional to the number of oranges. Like question 5, question 8 can’t be solved using proportional reasoning.
To round off the activity, bring the groups together to summarise the eight questions in terms of the learning outcome. Highlight the importance of thinking about the context and looking for answers that are sensible, instead of unthinkingly multiplying or dividing.

Answers to Activity

1. 160 g is of 800 g. The amounts are all in proportion to each other:
1/5 of 400 is 80 g of rolled oats
1/5 of 250 is 50 g of bran flakes
1/5 of 150 is 30 g of dried fruit.
2. There is no way of knowing. The theoretical probabilities for each colour are: black 3/10, white 1/10, pink 1/5, yellow 3/20, blue 1/4.
Using this information, you could predict that your 50 would be made up in this way: 15 black, 5 white, 10 pink, 7 or 8 yellow, and 12 or 13 blue. But it is extremely unlikely that this is exactly what you would get. You would get a different result every time you tried.
3. 10 days. (30 ÷ 3 = 10)
4. 61. (20 x 3 + 1 = 61)
5. 10 km is 100 times as far as 100 m, but André will not be able to run 10 km in 100 x 15 s (1 500 s = 25 min). This is because a runner can’t keep up a sprint speed over a long distance. All that can be said for certain is that André will take longer than 25 min to run 10 km.
6. 32 g. (Twice the amount of sugar in the Feisty bottle is 48 g. Trim ’n’ Slim has 2/3 of this, that is, 32 g.)

7. $2.50. (If 6 oranges cost $1.50, 1 orange costs 25 cents, so 10 oranges cost 10 x 25 cents = $2.50.)

8. There is no way of knowing for sure. For one thing, the boats will have different lengths and weights. The pairs will probably be slower than the fours, but not twice as slow. The eights will probably be faster, but not twice as fast.