Branching Out
This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (343 KB)
multiply decimals with multiples of ten
operate on fractions and decimals
Number Framework Links
Use these activities to:
• help your students to consolidate and apply advanced additive and advanced multiplicative part–whole strategies (stages 6 and 7) in multiplication and division of whole numbers
• extend the students who are beginning to use proportional part–whole strategies so that they become confident at this type of thinking.
FIO, Level 3, Number Sense and Algebraic Thinking, Book One,Branching Out, pages 10 -11
In these activities, students identify patterns and relationships between equations. They explore the effects of proportionally adjusting number expressions.
Students need to be at least advanced additive part–whole thinkers (stage 6) to do this activity independently. They should be familiar with fractions and decimal fractions and multiplying and dividing by multiples of 10 and 100.
Students working independently will need to work in pairs or groups of 3 to complete parts of this activity and will need photocopies of the web copymasters to work on.
You may need to define these terms:
• Expression: symbols connected by an operator (+, –, x, ÷) with no equals signs, for example, 40 x 6 or 69 + 8.
• Relationship: how any two things (in this case, expressions) are connected, how changing one changes the other, and what patterns you can see.
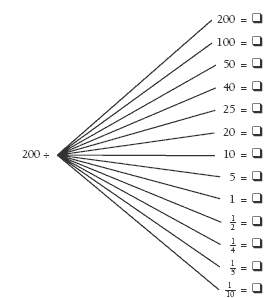
Activity One
Encourage the students to change the expressions around to make them easier to solve. For example:
If you know “something divided by 10 is 100”, how could you change this into a multiplication problem that
could help you? ( ÷ 10 = 100 has the same answer as 10 x 100 =.)
Students who don’t have a strong grasp of multiplicative strategies may need to confirm their predictions on a calculator after they make each one because it is impossible to identify useful patterns based on inaccurate answers. Encourage them to build on this instant feedback by looking for patterns and using them to predict related answers.
Asking your students questions about the relationships between the webs will help them to focus on identifying patterns they can use to predict answers:
What connections can you see between the 100 and the 200 webs?
What do you have to do to that number to make it into this new number?
Is it the same for the other spokes on the web?
Which ones are different?
Note that the relationships between the expressions are not as simple as they first appear. For multiplication expressions, when the answer is doubled, all the boxes in the multiplication expressions are doubled. In the division expressions, the action depends on the position of the . Where the is the divisor, for example, 200 ÷ , doubling the answer is matched by halving the box number.
There are three key issues here:
• Division is not commutative (reversible). 8 ÷ 4 is not the same as 4 ÷ 8.
• Increasing the variable () in ÷ 10 increases the result by the factor of the increase (because 1/10 of something big is always greater than of something small).
• Increasing the variable in 10 ÷ decreases the result proportionally, for example, 10 ÷ 2 is twice 10 ÷ 4 because the more people there are sharing the 10 items, the less they each get.
These ideas can be easily demonstrated using examples.
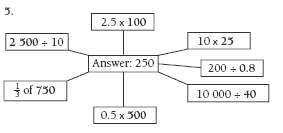
Question 5 is a useful formative assessment checkpoint for algebraic thinking. Do the students use the multiplicative relationships they have discovered, or are they still needing to guess and check the answers? Students who understand the patterns and relationships they have been exploring in questions 1–4 are likely to see that they can solve most of the questions by multiplying their answer to question
1 by 2.5. However, most will have trouble with 200 ÷ = 250 and may wonder “How is it that a number can become bigger by dividing?” One approach you could take to this is to ask your students to complete the pattern in the following:
Once they realise that the number they are looking for in 200 ÷ = 250 is less than 1, they can search for it using trial and improvement. Another approach is to see 200 ÷ 1/2 as How many halves do you get in 200? This explains the answer of 400 (halves). The unit of the answer is the real issue: it’s not ones, it’s halves.
Activity Two
In question 1, students are asked to identify patterns in each branch of the web so that they can continue the same pattern. This familiarises them with the various ways that expressions can be adjusted to make them easier to solve without changing the answer. This can be helpful when solving problems mentally. The branch 20 ÷ 1 →10 ÷ 0.5 continues to explore division by numbers less than 1 (but greater than 0).
Challenge the students to use fractions and decimal fractions for the ? branches of the big web. Get them to check each other’s webs by using a calculator to do the equation on the end of each branch.
To encourage reflective discussion, ask the following questions in a think-pair-share discussion:
Did you use any short cuts today that helped you predict the answers?
What patterns did you notice that would be useful to remember?
Did any patterns surprise you?
Why might it be useful to change expressions so that they have different numbers that still give the same answer (like you did on your big webs)?
Answers to Activity
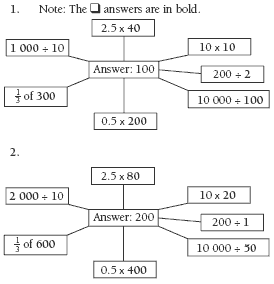
Activity One
3. You could change your answers from question 1 by halving the amount when it’s a multiplication expression or when it’s ÷ 10 and doubling the amount in the other division expressions (where the is the divisor, not the dividend, as in 100 ÷ ).
The web would look like this
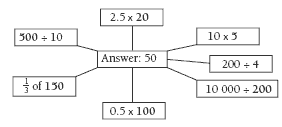
4. Answers may vary. The multiplication numbers and the ÷ 10 numbers in the 50 web are those in the 100 web, and those in the 200 web are double those in the 100 web.
The other division numbers in the 50 web are double those in the 100 web, and those in the 200 web are halved.
Activity Two
1. For the 2 branches that begin with 4 x 5: One factor is halved and the other is doubled each time. For the branch that begins 10 + 10, 9.9 + 10.1: 0.1 (or 1/10) is taken from one addend and added to the other each time. For the 2 branches that begin with 20 ÷ 1: The dividend (the number being divided) and the divisor (the number doing the dividing) are halved or doubled each time. So for all the branches, what happens to each number in the expression happens to all the numbers in the
same position in that branch.
2. The 4 x 5 branches can be extended to 0.25 x 80 and 32 x 0.625 (or 32 x 5/8).
The 10 + 10 branch can be extended to 9.8 + 10.2, 9.7 + 10.3, and so on.
The 20 ÷ 1 branches can be extended to 2.5 ÷ 0.125 and 160 ÷ 8.
Answers will vary for the 2 branches with ? in them. Check yours on a calculator