Comparing areas
Purpose
The purpose of this activity is to support students in attending to area (flat space) when comparing two shapes. Students are encouraged to use direct comparison by laying one shape on top of another.
Achievement Objectives
GM2-1: Create and use appropriate units and devices to measure length, area, volume and capacity, weight (mass), turn (angle), temperature, and time.
Required Resource Materials
- Copymaster (print and laminate then cut the flounder out)
Activity
- Introduce the flounder from the Copymaster - Fiafia and Fatu. Students may know that the fish is a flounder (called pātiki in Māori). Pātiki are a type of flatfish so they are very thin and have both eyes on the top of their head.
- Ask: Which flounder, Fiafia or Fatu is the biggest?
- Allow students to discuss this, in pairs, before discussing the questions as a class.
- Can you convince me you are right?
- Look for students to directly compare the fish by placing one on top of the other. Fiafia is longer than Fatu so students who confuse length with area will still choose the correct answer.
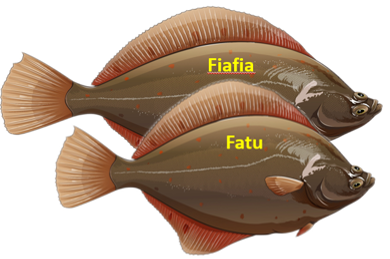
- When we compare the size of two pātiki do we just look at how long they are?
Raise the possibility that the width of the fish might also be important.
- Similarly compare the lengths of the pātiki called Fred and Felicity. These fish are the same length but clearly Felicity is bigger than Fred.
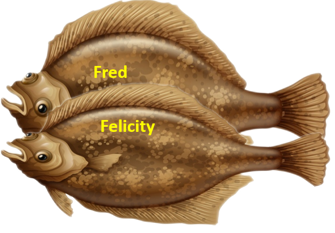
- Why is it that these flounder are the same length, but one is bigger than the other?
- Look for students to explain that the width of the fish must also be considered when comparing them by size. Overlap the fish to show that the lengths are equal, but Felicity is wider than Fred.
- Summarise that the size of a flounder depends on both how long and how side the fish is.
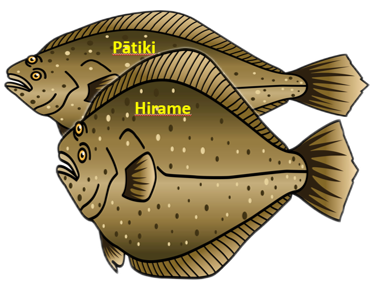
- Compare the other two pairs of fish, Finlay and Fiona, and Pātiki and Hirame (Japanese for founder). Both pairs have differences in length and width of the fish.
- Finlay is shorter than Fiona, but she is wider.
- Pātiki is longer than Hirame but not as wide.
- Let students discuss how to decide which fish is bigger. Look for a student to suggest that the area must be equal, the same. Another student may suggest that ‘taking and giving’ overlapping parts to make the fish about the same width or length might work.

- Provide students with a copy of Pages 3-4 of the Copymaster, scissors and tape. Initially, you might model completing one of the puzzles for the class, or use a guided approach to help students solve one of the puzzles. Consider grouping students strategically to encourage tuakana-teina.
- These puzzles can be solved in two directions. In the example below the L shape can be cut up and reformed to make the pentagon (house shape) or the pentagon cut up and reformed to create the L shape.
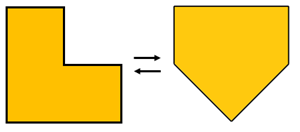
- The purpose of the puzzles is to develop students’ understanding of conservation of area (horahanga). Shapes can be reformed into other shapes with the same area, amount of flat space. Often shapes that look to have different areas but have the same area.
Next steps
- Provide students with experiences where the spaces are of similar area, and one shape can be modified to make the other shape. For example, a ‘give and take’ approach can be used to show that the shapes, in each of the pairs below, have the same area.
- Have students find two dimensional shapes in their environment and compare the areas of the shapes.
Attachments
comparing-areas.pdf545.24 KB