Comparing ratios with a common part
Purpose
The purpose of this activity is to support students in comparing ratios with a common part but different whole. They do so by creating and comparing fractions.
Achievement Objectives
NA4-3: Find fractions, decimals, and percentages of amounts expressed as whole numbers, simple fractions, and decimals.
NA4-4: Apply simple linear proportions, including ordering fractions.
Required Resource Materials
- Connecting cubes
- Calculators
Activity
- Pose a ratio comparison where the number of cubes in one part is the same but the whole is different.
Here are the ratios 2:3 and 2:4. Which mixture has the strongest taste of blueberry?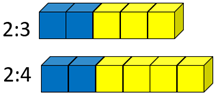
Expressing the part to whole relationships as fractions allows the comparison.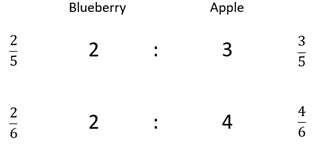
Since 2/5 is greater than 2/6, because fifths are larger than sixths, it can be claimed that 2:3 has a slightly stronger taste of blueberry than 2:4. Write the inequality 2/5 > 2/6.
Which ratio tastes most strongly of apple?
Students should recognise that a stronger taste of blueberry means a weaker taste of apple. Looking at the fractions confirms that that is true for these ratios: 3/5 is less than 4/6 so 2:4 has a stronger taste of apple than 2:3.
You might use a calculator to confirm the inequality, using the operations 3 ÷ 5 = 0.6 and 4 ÷ 6 = 0.666, to change 3/5 and 4/6 into decimals. Write the inequality 3/5 < 4/6.
- Pose further problems with one part of both ratios being the same and the wholes being different. Use familiar fractions to make the inequalities easier to see. If needed, use a calculator to confirm the inequalities. Write the inequalities as you work through each problem. Good examples might include:
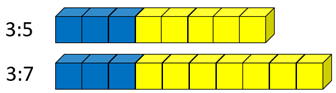
- Which has a stronger taste of blueberry 3:5 or 3:7?

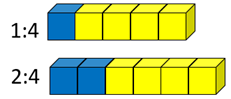
- Which has a stronger taste of blueberry 1:4 or 2:4?

- Which has a stronger taste of blueberry 4:8 or 4:6?
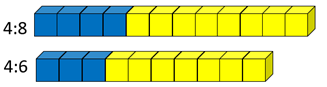
- Which has a stronger taste of blueberry 4:6 or 6:6?
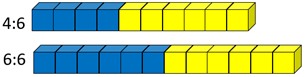
- Which has a stronger taste of blueberry 3:5 or 3:7?
Next steps
- Increase the level of abstraction by progressing from using fraction strips to diagrams to symbols only. Maintain the types of ratios in the lesson description until students make the comparisons using the symbols alone.
- Progress to comparison problems involving a mixture of common part and common whole. Support students to discriminate between these types of problems. For example, you might provide this suite of ratio comparison problems, using blueberry and apple juice as a context:
Which mixture tastes most strongly of blueberry?
Note the first number represents parts that are blueberry and the second number represents parts that are apple.
3:4 or 6:8? (equivalent ratios so equal flavour)
5:3 or 5:2? (equal part)
5:7 or 4:8? (equal whole)