Simple discounts
Purpose
The purpose of this activity is to support students in calculating prices after a simple percentage discount is applied.
Achievement Objectives
NA4-3: Find fractions, decimals, and percentages of amounts expressed as whole numbers, simple fractions, and decimals.
Required Resource Materials
- Connecting cubes
- Paper and pens
- Calculators
Activity
- Use cube stack models to revise common fractions as percentages.
What percentage of each stack is yellow? What percentage is blue?
5/10 = 1/2 = 50%
3/12 = 1/4 = 25% 9/12 = 3/4 = 75%
4/5 = 8/10 = 80% 1/5 = 2/10 = 20%
6/10 = 3/5 = 60% 4/10 = 2/5 = 40%
3/8 = 37.5% 5/8 = 62.5%
- Pose this problem:
You go to a shop and buy an item that usually costs $40. They have a 20% off sale.
How much do you pay for the item? You might adapt this problem to include a more specific context that is more relevant to your students' interests, cultural backgrounds, and learning from other curriculum areas.
Draw a double number line to represent the problem:
What percentage is taken off? (20%)
What percentage of the price do you pay? (80% since 100 – 20 = 80%)
How much is 10% of $40? (10% = 1/10 so 10% of 40 = $4)
How much is 20% of $40? (20% = 1/5 or 2/10 so $8 is taken off)
What is 80% of $40? (8 x $4 = $32 or 4 x $8 = $32)
Develop the double number line as each question is answered.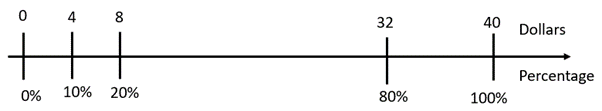
- Pose similar problems and support students to create double number line models to find the answers. Organise students in groupings that will encourage peer scaffolding and extension, as well as productive learning conversations. Examples might be:
- You go to a shop and buy an item that usually costs $70. They have a 50% off sale.
How much do you pay for the item?
Students might use 10% of 70 = $7 and multiply that answer by five to get $35 or recognise that 50% = 1/2 so find 1/2 x 70 = $35.
- You go to a shop and buy an item that usually costs $88. They have a 25% off sale.
How much do you pay for the item?
Students might recognise that 25% = 1/4, find 1/4 x 88 = $22 and subtract that amount from 88 to get $66. They might find 1/4 x 88 = 22 then multiply that amount by three to get 3 x 22 = $66.
Alternatively they might use 10% of 88 = $8.80 so 5% of 88 = $4.40. They might then subtract, 88 – 8.80 – 8.80 – 4.40 = $66.
- You go to a shop and buy an item that usually costs $55. They have a 30% off sale.
How much do you pay for the item?
Students might recognise that 30% equals three times 10%, find 1/10 x 55 = $5.50, 3 x 5.50 = $16.50, and subtract that amount from 55 to get $38.50.
Alternatively they might use 10% of 55 = $5.50 so 70% of 55 = 7 x 5.50 = $38.50.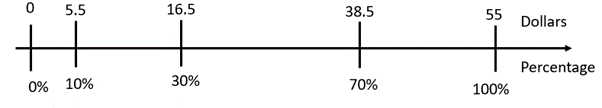
- You go to a shop and buy an item that usually costs $90. They have a 45% off sale.
How much do you pay for the item?
Students might recognise that 45% equals 40% and 5%. They might find 1/10 x 90 = $9, 4 x 9 = $36.00. 5% equals half of 10% which is $4.50. Then they find that 45% equals 36 + 4.50 = $40.50 and subtract that amount from 90 to get $49.50.
Alternatively they might use 10% of 90 = $9 so 5% of 90 = $4.50. 11 x 5% = 55% which equals 11 x 4.5 = $49.50
- You go to a shop and buy an item that usually costs $70. They have a 50% off sale.
Next steps
- Introduce using a unit rate on the calculator as another useful strategy. For example, to take 25% off $200, we must recognise that the remaining percentage is 75% (100 – 25), before calculating 200 ÷ 100 = $2 to work out that 1% equals $2.00. We multiply 75 x 2 = $150 to get the price that is paid.
- Explore more difficult examples of discounts with percentages that are equivalent to thirds and eighths. For example, to take off 33% from $60, we must recognise that 33% is very close to one third, before calculating 1/3 x 60 = $20.00 to work out the amount to be taken off. We subtract 60 – 20 = $40 to get the price that is paid.