Session 1

1. To begin the week we will use some simple experiences that will reinforce the students’ existing knowledge of units of capacity and will provide an assessment of their initial knowledge.
2. Pose the problem below. This could be adapted to suit the context of your class. Instead of a birthday party, the context for this session could be “how many bottles of juice need to be purchased for the school disco?” or “how many bottles of water need to be provided to the waka ama team?”
   Marama is planning her birthday party.
   She wants to invite eleven friends so there will be twelve people at the party.
   How many bottles of soft drink will she need to buy so that each person can have one drink?
3. Discuss this problem with the class. Students will have ideas like: It depends on the size of the bottle. (What sizes can you get? 600 mL, 1.25 L etc.) It depends on the size of the cups/glasses.
   (How much does a cup hold? 200mL, 250 mL, 300 mL, etc.)
   It also depends on how much you are going to fill each cup.
   
   Establish the capacity of a single cup, by measuring the amount of water it holds up to a suitable level. Pour the water into a measurement jug and read the scale. 
4. Produce a 1.5 litre bottle full of water and a 250 mL cup. Get the students to estimate how many full cups of drink they believe could be poured from the bottle. Ask individual students to give their estimates and explain their thinking. Record the estimates on a dot plot with each dot representing an individual student's estimate.
   
   
   Pour one cup of water from the bottle and invite the students to change their estimates if they wish. If the dot plot has been made with sticky dots on a whiteboard they can easily be rearranged.
   Confirm the actual number of cups the bottle holds by pouring until it is empty. Compare the actual result to their estimates on the dot plot and invite them to explain what they notice.
5. Remind the students of Marama’s birthday problem and tell them that they are going to solve her problem in groups. Each group will be given a full bottle of water, an icecream container (for catching spillage), and a cup. They are to work out how many bottles Marama will need, by estimation first, then confirm their estimation by pouring. Note that different groups will use bottles of different sizes. Remind the students to record their results for reporting back.
6. Allow the groups time to attempt Marama’s problem then bring them together for reporting back. Focus on their methods of estimation, particularly how they may have applied the results from the introduction.
7. Ask if there is an easier way to find out the number of cups that can be poured from each bottle. Using comparisons from one metric unit to another may help the groups solve Marama’s problem. For example, a student may say that you can get ten 250mL cups from a 2.5 litre bottle since 2.5 litres equals 2500 millilitres.
8. The groups then reform to use metric units to solve Marama’s problem with the bottle and cup from another group. For example, given a 1.5 litre bottle and a 250 mL cup they should work out that the bottle will hold six cups (6 x 250 = 1500mL) with 50 mL to spare. Marama will need two bottles in this case. The students’ answers can be checked, as before, by repeatedly pouring.
9. Get the students to write a sentence or two in their book/journal telling you what they now know about the metric units of capacity. Their reflections can be used to gauge their initial knowledge. Invite ideas from them to make a chart about metric units. Key comparisons are 1000 millilitres ( 1000 mL) = 1 litre (1 L), 500 mL = 0.5 litres, 250 mL = 0.25 litres, etc.

Session 2

1. For the next three days we put the students in situations where they need to apply their knowledge of the metric units for capacity. They will be required to make sense of an unknown system and compare it to our own.
2. Tell students that there is a tiny island nation, called Smati, in the South Pacific Ocean. The people of Smati have a special elixir that helps people to remember their multiplication and division tables. (Wouldn’t you like some of that?) You are going to go on a trade mission to Smati so New Zealand can trade our milk for their elixir. Unfortunately, on Smati they do not use litres and millilitres to measure capacity. They use sloshes, dribbles, and plops. Before you can go to Smati you will need to figure out how big each unit is so that you can talk their language (of capacity, that is).
3. Tell the students that you have some bottles of elixir from Smati which give some clue about how many millilitres or litres a slosh, a dribble and a plop are. You will need to have prepared a measurement jug and the following full bottles of "elixir" for each group:
   600 mL labelled 12 dribbles, 1 litre bottle labelled 4 plops,
   1.5 L labelled 1 slosh.
   In their groups students are to find out how they can change measurements in dribbles, plops and sloshes into metric units. Remind them to record their results.
4. While the students are investigating, circulate around the groups to monitor their progress. Important guiding questions are:
   Which Smati unit do you think is biggest? Why?
   Which Smati unit do you think will be easiest to compare with our own units, litres and millilitres? Why?
   How do you think dribbles, plops and sloshes are related?
   How could you find out how many millilitres are the same as one plop?
5. After a while bring the class together with the intention of making a conversion chart for Smati measures to metric measures. Get different groups to report back and look for common findings. These can be confirmed by checking with the bottles:
   12 dribbles = 600 mL, so 1 dribble = 50 mL
   4 plops = 1 litre = 1000 mL, so 1 plop = 250 mL
   1 slosh = 1.5 L = 1500 mL
6. Ask: How many dribbles would make a plop? (5)
   How many plops make a slosh? (6)
   How many dribbles make a slosh? (30)
7. Give each group a 2 litre milk bottle. Tell them that it needs to be relabelled so that Smati people will know how much milk it holds. Send them away to figure out the new label. Report back on their ideas. Note that many answers are possible like, 1 slosh and 2 plops, 40 dribbles, 8 plops. Discuss which label might be best.

Session 3

1. Have a range of plastic bottles of many different sizes for the students to use. Provide sticky labels.You may need to discuss why bottles are certain sizes. This brings up ideas of suitability for purpose (technology curriculum) and tidiness in terms of units of capacity (348 mL is not a common bottle size!).
2. Tell the students that they must come up with a new range of milk bottles for the Smati market. Each bottle must be labelled with how much milk it holds in dribbles, plops, and sloshes. Consumers in Smati like the capacities to be both functional and easy to recognise. Discuss what milk is used for.
   How much milk does your household use?
   What size bottles does your family buy?
   Why is that size good for your needs?
3. Once each group has its range of milk bottles another group can adopt the role of the Smatian customs inspectors to check that each bottle is the capacity that is stated.
4. Now for the trade mission to Smati! Tell the students that when you go to Smati the trade rules are half as much elixir of the same volume of milk. So, if you give them a two plop bottle of milk, they will give you a one plop bottle of elixir. Use the milk bottles the students have created and pretend they are taking this milk to Smati. They must find out how much elixir, in millilitres and litres, they will receive back for the milk they are taking. This may be done by acting out with one group as New Zealanders and the other as Smatians!

Session Four

1. It is good to trade with Smati as kiwi students desperately need the elixir to help them remember multiplication and division facts. However, pricing the bottles of elixir for the supermarket might get quite complicated. Provide bottles of different shapes and capacities for students to use.
2. Remember that New Zealand exchanges milk for elixir so the prices need to be comparable.
   What should be true about the price of a bottle of elixir?
   Students should say that elixir is twice as expensive as milk for the same volume.
   What does milk cost?
3. You might look online for the current price of milk. That price will vary depending on the size of the bottle. A 1L bottle might cost $2.65 while a 2L bottle might cost $4.90.
   Is that the same amount for every 100mL? How could we find that cost per 100mL?
4. Discuss how dividing the price by the number of mL gives the cost per millilitre. Multiplying that unit cost by 100 gives the price per 100mL. Confirm that smaller bottles usually cost more per 100mL than larger bottles.
5. Pose the problem:
   A Supermarket is now importing Smarti elixir. They wonder how much they should charge for a bottle.
   How could they work out what to charge?
6. Students might say that the price depends on the size of the bottle.
   Take a specific bottle as an example (say a 3L juice bottle)
   Ask: It says that this bottle holds 2 sloshes. Does that information help? What other information do we need?
7. Students might suggest converting the Smati measure to millilitres. (1 slosh = 1500mL so 2 sloshes equals 3000mL)
   So we should charge the cost of 3000 mL of milk? Have we forgotten something?
   3000mL of elixir was traded for twice as much milk, 6000mL. How much does 6000mL of milk cost?
8. Students need to convert 6000mL into 6 litres and calculate the cost of three 2L bottles of milk.
   The pricing of bottles takes two steps:
   • Each group chooses a set of five bottles in various sizes and shapes. They work out the Smati measure of capacity for each bottle and label it accordingly. e.g. 4 Plops for 1L.
   • Groups exchange sets of bottles and the receiving group must work out the correct price to charge for each bottle full of elixir. Someone in the group acts as the recorder so that the calculations are clear.
9. After a suitable time, ask the groups to offer one bottle with a displayed price to the class collection.
   Do the prices look right?
10. The discussion might raise issues about estimating the capacity of bottles, especially those that are irregular. Students might also question some calculations.
    Which prices look correct? Which prices are possibly incorrect?
11. Check on dubious prices (Could be the Consumer watchdog or Fair Go).
12. If time permits, investigate how long a bottle of elixir from Smati will last.
    To improve your basic facts it is recommended that you drink 20mL of elixir per day. 
    How many days do these bottles of elixir last at that rate?

Session 5

1. Get the students to bring along the oddest shaped plastic bottles they can find. Shampoo and fruit juice bottles are good examples. With the whole class choose three or four bottles of different shapes but similar sizes. Label them A, B, C, D. Tell the students to rank them in order of capacity by sight and record their beliefs. Pour 100 mL of water from each bottle and mark the level with a felt pen (some bottles will not be very transparent).
2. The students now revise their order and estimate the total capacity of each bottle. Discuss their methods of estimation, particularly their use of the 100mL as a benchmark and observations about the shape of the bottle at different points. Get a student to pour the remaining contents of each bottle into a measuring jug to check.
3. Put the students into groups of four with several different odd shaped bottles. Their task is to make marks on each bottle to indicate fair shares of the bottle into quarters. They may use a capacity measure to do this if they wish. This will provide excellent assessment information about their ability to apply the metric units. For example a 600mL bottle could be marked in divisions of 150mL.

Getting Started

In this session students explore how the same data can be shown on a bar graph and a pie graph. They take a bar graph and rearrange it to make a strip graph and then use it to draw a pie graph.  At the end of the session the students will have 3 graphs of the same data.

1. As a class, decide on a simple, meaningful topic to collect data about as a class. Try to frame this in response to the current learning interests or events that are a part of your students’ lives (e.g. a school camp, Polyfest). Examples could include favourite sports, method of transport to school, or food usually eaten for breakfast.
2. As a class, come up with a survey question to ask to the class (e.g. what activities are our class members most looking forward to on school camp?) Explain to the class that we are looking to find categorical data - meaning data that looks at different groups or categories, and describes the quality of something. For this question, the different camp activities would be the quality measured. 
3. Conduct a survey as a class. Model collecting this data in an organised and logical manner. You could use a paper template, or Google Sheet to do this.
4. Model how to enter this data into Microsoft Excel or Google Sheets. You will need to add the categories (e.g. the activities on school camp) to one column - with one option in each cell. In the column to the right, record the numbers of students that preferred each activity.
   • If you are using Microsoft Excel, select all of the data in both columns, choose the Insert tab, click the column graph icon () and choose the top left option (clustered column graph). Using the chart design tab you can change the format and appearance of the graph.
   • If using Google sheets, select all of the data in both columns and click insert → chart from the menu bar. A pie graph will appear. Using the chart editor, you can change the format and appearance of the graph.
5. Support students to create their own bar graph - individually or in pairs. Ensure that they add a title and axis labels. If your students are ready to be extended, they could come up with a new question to investigate.
6. Print two copies of the bar graph you created with the class.
7. Ask the students to take one copy of the graph and cut up the bars. Using sellotape students stick the bars end to end to form a strip graph.
8. Discuss the two graphs with the students. For example, ensure that they recognise that that the same data is shown on both graphs.
9. Ask students to take the strip graph, put it on its edge, and join the two ends to make a circle. By drawing a line from the circumference where the colour changes on the strip graph to the centre of the circle students can mark the sections of a pie graph. Students should then colour the sections of the pie graph to match the colours of the strip graph. 
10. Discuss with the students that the 3 graphs all show the same data.

Exploring

Choose a graph

Activity 1

Refer to the bar and pie graph that students constructed in the previous session.
Ask the students questions, and ask which graph they used to answer the question:
For example: How many children walk to school? Which graph shows this best?
What percentage of children travel by car?
The school thinks about a third of the children come by bike, is this true?
How many more children come by bus than by car?

Discuss with the students why bar graphs are useful for showing the number of items and why pie graphs show proportions well.

Activity 2

Students are to make a bar graph and a pie graph for favourite spreads using the percentages given in the table below.

Check that they include titles on both graphs and labels on the axes of the bar graph.

Ask the students which type of graph they would use if they want to show:

• 15% of the children in the survey like jam.
• Over a third of the children picked nutella.
• 10% more children like honey than like jam.
• The most popular spread is nutella.

Lucky Dip

1. Organise the students into groups of 4. Cut out the lucky dip cards in Copymaster 1 and have the students take turns at selecting a card from a container. Use all the cards. 
2. Have students construct a bar graph and a pie graph of the data using Excel or Sheets.
3. Students discuss and decide which graph is best for answering the following questions about the data.
   1. How many bouncy ball prizes are there?
   2. Which prize is about a third of all the prizes?
   3. Are there more bouncy balls or pencil prizes?
   4. What prize is 25% of all the prizes?
   5. How many more lollipop prizes are there than yoyo?
      Students are likely to have answered questions a, c and e using the bar graph, and questions b and d using the pie graph.
4. Ask students to use the questions and answers to write appropriate statements about the data under each of the graphs.

Writing and evaluating statements

1. Students complete a bar and a pie graph by choosing their own topic and categories. As a class, brainstorm a list of topics and categories that students could explore. 
2. Ask students to write statements under each graph. Remind students that the graph should clearly illustrate their statement.
3. Ask students to exchange their work with a buddy and check that the statement is true and is clearly shown by the graph.

Reflecting

In this final session students evaluate if statements are true about a graph and if the graph clearly illustrates the statement.

1. Using the data in the table below, students construct a bar graph and a pie graph of "Favourite things to do in the school holidays".

   Favourite thing to do in the school holidays	Percentage
   Holiday with family	40
   Playing computer games	15
   Going to holiday programmes	20
   Playing with friends	25

2. Ask them to complete the Statements Table on Copymaster 2.
3. After working by themselves students compare their answers with a classmate.

Session 1

In this session students learn to use a cup containing cubes to represent a variable.

1. Put two plastic cups of different colours on a table. Tell the students that you are going to put 12 cubes into the cups. Ask, “How many cubes might go in each cup?”

2. Draw up a table of values to organise the students’ responses. Note that students frequently neglect the options that have zero cubes in a cup. This task is an excellent opportunity to develop the concept of zero as the numbers representing ‘nothing of something.’ 

   Blue	Green
   0	12
   1	11
   2	10
   3	?

3. Tell the students to draw a graph to show the relation between the number of cubes in the blue cup and how many are in the green cup. Ask them to predict what the graph might look like. Students might hand draw the graph or use a spreadsheet like Microsoft Excel or Google Sheets to complete it. If necessary, you could model the construction of a graph, and then have students create their graphs independently or with their peers. This could also be done as a whole-class teacher-modelled activity.
   Ask students to explain why they think the points on the graph lie along a downward sloping straight line. They might notice that the value of the green cup variable goes down by one as the value of the blue cup variable goes up by one.
   

4. Using a range of different coloured cups and different numbers of cubes pose similar problems asking the students to come up with a table of values and a graph to represent the relations. The table below shows four examples of possible problems. The students should model the situation with actual cups and cubes to come with ordered pairs such as (1,3) to represent possible values that the variable may assume. Note that you are dealing with discrete variables (i.e. random variables that can take only distinct values, usually whole numbers). Therefore, the numbers of cubes should be whole numbers. Some students may consider fractions of cubes. Examples of useful relations might be:

   The red cup has two more cubes than the blue cup. This linear relation is effectively r = b + 2	Each blue cup has the same number of cubes. The number of cubes in the yellow cup equals the total number in both blue cups. This linear relation is effectively  y = 2b (b multiplied by 2)
   There are 18 cubes in total. Each yellow cup holds the same number. This linear relation is effectively 18 = r + 2y	The number of cubes in the yellow cup equals the total number of cubes in all the blue cups. This linear relation is effectively y = 3b (b multiplied by 3)

5. Note that in some of these relations, an infinite number of whole number values could be put in the table. For example, in the problem with one yellow cup an three blue cups, the table could read:

   Blue cup	Yellow Cup
   0	0
   1	3
   2	6
   3	9

6. Ask the students to come up with rules that describe the relation. If necessary, model coming up with a rule as a class. You could organise students to work in tuakana-teina relationships, and give students the option to work with the teacher for more direct support. For the relation above this might be, “There are three times as many cubes in the yellow cup as there are in each compared to the blue cup.” Algebraically, this might be recorded as y = 3b, though this is not a learning intention for students at this level. Using algebraic conventions to represent the rule for a pattern could be offered as an extension task. Choose a couple of relations for students to graph. Look at the pattern formed by points on the graph and ask students to explain why the graph is linear (it points in a straight line).
7. Pose real life scenarios for students to support them to understand the significance of relationships with variables. Model each scenario with cups and cubes, with a particular coloured cup representing the number of items possessed by each person.
   • Tammy is four years older than Hosepha. How old might both people be?
   • Anshul has three times as many toy cars as Kahu. How many toy cars might each boy have?
   • Altogether Liam and Moana have 24 video games. Moana has twice as many video games as Liam. How many games might each person have? (Note that zero values are not possible in this problem. Why?)

Session 2

In this session students explore the effect of operations on variables. Inverse operations are presented as “doing and undoing” processes.

1. Pose “think of a number” problems for students that result in some unexpected answers at the end. Encourage the students to reason why that occurs and discuss with a partner. The processes involved can be modelled using cups and cubes. Begin with a problem where the use of inverse operations is obvious. Note that the algebraic representation is not expected though you might use an empty box as n for a more accessible representation.

   Instructions	Cups and cubes model	Algebraically
   Think of a number		n
   Add five		n + 5
   Take away your starting number		5

   Ask: Why does everyone get an answer of five, no matter what starting number they thought of?
   Do your students realise that subtracting n undoes the adding of n in the first place?
    

2. Develop more complex examples. Encourage the students to model the steps with cups and cubes to explain the effect of the operations.
   For example:

   Instructions	Cups and cubes model	Algebraically
   Think of a number greater than 5		n
   Take away four		n – 4
   Double the answer		2 (n- 4) = 2n – 8
   Add ten		2n + 2
   Halve the answer		n + 1
   Take away your starting number		1
   Your answer is one!

   Instructions	Cups and cubes model	Algebraically
   Think of a number		n
   Add three to the number		n + 3
   Double the answer		2(n + 3) = 2n + 6
   Take away four		2n + 2
   Halve the answer		n + 1
   What number did you start with? Your final answer was one more than your starting number.

3. Discuss how each activity works. Look for students to explain that some operations undo others. In particular, subtraction undoes addition (and vice versa) and division undoes multiplication (and vice versa). 
   Tell your students that addition and subtraction, and multiplication and division are inverse operations. With the class, come up with a list of metaphors that describe inverse relationships (e.g. turning a light switch on and off).
   Students also need to recognise when an operation is only partly undone. For example, with 3n + 6 dividing by three will undo multiplying n by three, but the addition of six is not completely undone. Demonstrate this for students.
4. As a class, come up with a new (or several) “think of a number” problem(s) and represent the values in a table and graph. Highlight that the relationship on the graph is linear (i.e. is represented by a straight line). Emphasise the use of inverse operations, and draw on students’ experiences of working with cups and cubes. Keep the equations simple by using only two different operations, and numbers below 10 (e.g. 4n + 7). The letter ‘n’ can be used to keep the equation(s) consistent with what has previously been covered in the lesson.
5. Invite the students to develop their own “think of a number” problems. This could be done in pairs, small groups, or independently. Emphasise the use of inverse operations. At this stage, students are not expected to find the resulting answer of linear equations, rather they are expected to demonstrate their understanding of the effects of operations. Their attempts can be set as examples for other students to explain. Look for the following:
   • How complex are students’ attempts at inverse operations? In the early stages you will find that students tend to immediately undo a previous operation.
   • How comfortable are your students with variables being unknown?
   • Are they able to recognise the parts of an expression that are variable (the cups) and that are fixed (the cubes)?
   • Can they control variables and numbers under the operations? Division is particularly challenging. For example, 3n + 6 divided by three requires each part, 3 cups and 6 cubes, to be divided separately then recombined.

Session 3

In this session students model equality with cups and cubes models. They investigate operations that can be performed on both sides of the equation, that simplify the relationship while maintaining equality.

1. Begin with simple equalities such as:

   Each red cup has the same number of cubes and each blue cup has the same number of cubes. Which collection, left or right,  has the most cubes?
   Look for students to realise that structurally the collections are the same (Two blue cups and three red cups on each side). This can be provoked by putting different numbers of cubes into the cups, e.g. 3 cubes in each red cup, 8 cubes in each blue cup. The equality of the collections is preserved no matter what numbers are used.

2. Ask: Could I remove cups from both collections and the total number of cubes would remain equal? What could I do?
   Look for students to realise that taking away the same cups from each side leaves the equality maintained. Algebraically that is alike 3r + 2b = 2b + 3r so 2r + 2b = 2b + 2r (subtracting one red cup from each side)
   Also consider what cannot be done. For example, removing a red cup from the left collection and a blue cup from the right collection does not maintain the equality. 

3. Provide other examples where applying the same operation to both sides makes finding possible values for the variables much easier.

   Each yellow cup holds the same number of cubes as every other yellow cup.
   Each blue cup holds the same number of cubes as every other blue cup.
   The left collection of cubes equals the right collection of cubes.
   What numbers of cubes could be in the yellow and blue cups?
   
   
   Simplifying both sides by removing the same cups makes the problem much easier.
   
   In this case students are left with the equality that one blue cup equals two yellow cups (b = 2y). An infinite set of solutions like (0, 0), (2, 1), (4, 2),… is possible.
    

4. Get students to connect the concepts of variable and equality using group worthy problems like:

   
   Each cup of a given colour, in both collections, must contain the same number of cubes, e.g. all reds hold 4 cubes, all yellows hold 3 cubes.
   What numbers of cubes could be put in each cup so that the two collections contain the same total number of cubes?
   Students might realise that the number of cubes placed in the red cups is irrelevant to the problem since it is the equivalence of two yellow cups to one blue cup that determines whether or not the collections are equal. They are likely to arrive at this conclusion by experimenting and looking for commonality among the solutions.

5. Recording their solutions systematically will help:
   Solutions for r = 1                              Solutions for r = 2                 Solutions for r = 3
   y = 0 so b = 0                                      y = 0 so b = 0                         y = 0 so b = 0
   y = 1 so b = 2                                      y = 1 so b = 2                          y = 1 so b = 2
   y = 2 so b = 4                                      y = 2 so b = 4                          y = 2 so b = 4
   y = 3 so b = 6                                      ....                                          ....
    
6. Explore other group-worthy equivalence problems such as:
   •                              
     What numbers of cubes for each colour of cup will make each collection equal?
     (Two reds must equal one blue plus six)
     What is in common with these solutions? 
      
   •                                
     What numbers of cubes for each colour of cup make each collection equal? (One green plus one blue must equal one yellow plus three)

Session Four

In this session cups and cubes models are created to solve problems more traditionally associated with algebra. Students attempt to find specific unknowns from the information they are given.

1. Start with this problem:
   Manaia began the weekend with some dollars in his money jar.
   He worked all day on Saturday weeding Mr Barkley’s gardens.
   After he was paid Manaia saw he had five times as much money as he had to start with.
   On Sunday, he delivered advertising, and made an extra $12.
   By the end of the weekend he had a total of $72.
   How much money did he have at the start of the weekend?
2. Ask students: How could we use cups and cubes to help us solve the problem?
3. Students might suggest using a cup to represent the amount of money Manaia had at the start. They might then track what happens to the model as Manaia earns money.
   
   Starts with some dollars…      Then has five times as much…Then adds $12 to that amount
    
4. Set up an equality like this (Equivalent to 5m + 12 = 72):
   
    
5. Ask: What can we do to make this equation simpler?
   Students should suggest some undoing, using inverse operations. The order is important. The undoing needs to occur in the reverse order to the first operations.
   Take $12 off each side:
   
   Divide both sides by five:
   
    
6. Manaia had $12 at the start of the weekend. Check the answer by acting out the original problem. Put 12 cubes in each cup then work through five times as much then adding $12.
   Has Manaia got $72 or are we incorrect?
   You might use a calculator to check (5 x 12 + 12 = 72)
7. Pose this problem for the students to solve in pairs. The numbers are smaller, but the operations are more complex. This problem could be adapted to better reflect your classroom context.
   Jodie collected lemons to squeeze juice. She started with a few lemons.
   After she visited her Nana’s tree, Jodie had six times as many lemons as she had to start.
   She got another 15 lemons from her neighbour.
   Jodie’s Mum was a bit worried about her lemon collecting habit. She told Jodie to share her lemons equally with her two sisters.
   “That’s fair,” said Jodie, “I still have 13 lemons to make juice.”
   How many lemons did Jodie have at the start?
8. Watch as your students try to model the problem.
   • Do they set up a cups and cubes model or find another strategy, e.g. trial and improvement?
   • Do they control the order of the inverse operations?
   • Do they check to see that their solution meets the conditions of the problem?
9. Gather the class to discuss strategies, and check the solution of four for the starting number of lemons.
10. Give your students Copymaster 1 to work through.  They can use cups and cubes if they want to model the problem though drawing diagrams is a useful alternative.
11. Students share their strategies with the class and justify their thinking.

Session 5

In this session students use the cups and cubes model to solve problems from growth patterns. Matchsticks are used to create the figurative patterns.

1. Connect the students’ understanding of equivalent structures with rules to describe relations. Pose problems like:
   Petra and Clive are looking at this matchstick pattern:
   
   They have worked out that it takes 25 matches to make 12 triangles in this way. Their teacher has challenged them to work out how many matches 100 triangles might take to make.
   What rules can you find to help Petra and Clive so they do not have to build 100 triangles?
   Students are likely to come up with different direct rules that describe the relation between the number of triangles and the number of matches. For example:
   • The first triangle took three matches. Each triangle after that took two matches. So to make 100 triangles takes 99 x 2 + 3 matches.
   • There was one match to start with and each triangle took two more matches. So 100 triangles takes 100 x 2 + 1 matches to make.
   • Each triangle takes three matches to make but when two triangles are joined there is one extra match. So to make 100 triangles takes 100 x 3 - 99 matches.
2. Ask the students to explain where the numbers come from in each person’s rule. Check to see that all three rules give the same answer to the number of matches. Use the explanations to model the structure of each rule using a cup to represent the chosen number of triangles.
   • Take one off the number of triangles (99), double it, and then add three. 
                            
      
   • Take the number of triangles (100), double it, and then add one.
     
      
   • Take the number of triangles (100), multiply by three, then take away one less than the number of triangles (99). Note 99 is the number of joins of two triangles and taking away one less than n is like taking n away but leaving one behind.
     
     With the cups and cubes model it is easier for students to appreciate the structural similarity of the rules in that one model can be converted to the others. For example, in the first rule if two of the three cubes are used to replace the two cubes taken out then the model becomes the second model. This is equivalent to proving physically that 2(n-1) + 3 = 2n + 1
3. Provide the students with a related stick problem and ask them to find as many rules as they can. Tell them to then explain the equivalence of the rules using cups and cubes models. For example:
   
   How many matches would it take to make 20 houses in this pattern?
   Rules might include:
   • 19 x 5 + 7 (seven for the first house, five for each house after that)
   • 20 x 5 + 2 (five for each house plus two matches to start)
   • 20 x 7 – 19 x 2  (seven for each house less two matches for each join)

Session 6 (extension session)

In this session students learn how cups and cubes models can represent why number relationships work.

1. Get the students to apply the structural strategies they have to problems that involve proof. Begin with simple properties of consecutive numbers.
   Take any three consecutive numbers, e.g. 3, 4, 5.
   If you add the numbers (3 + 4 + 5 = 12), this equals three times the middle number (3 x 4 = 12).
   Does this work for any set of three consecutive whole numbers? Why?
2. Invite students to explain why the rule holds for any set of consecutive whole numbers, and to model their explanation with the cups and cubes model.  Let n be the first number:
   
   Students may recognise that both collections total three lots of the first number plus three. Algebraically this could be written as, n + (n + 1) + (n + 2) = 3n + 3 = 3 (n + 1)
3. Pose another problem involving consecutive numbers and ask the students to explain why the property holds irrespective of which four numbers are chosen.
   Choose any four consecutive odd numbers, e.g. 3 + 5 + 7 + 9.
   Add the two outside numbers, e.g. 3 + 9 = 12.
   Add the two inside numbers, e.g. 5 + 7 = 12.
   Are the sums always equal no matter what consecutive odd numbers you choose? Why?
   Would this work for consecutive even numbers? Why?
    

4. Pose other more complex problems that can be modelled with cups and cubes.
   For example: 
   Choose any two single digit numbers, e.g. 3 and 8 (modelled by two different cups).
   Use the digits to make two different two-digit numbers,
   e.g. 38 and 83, 38 = 10 x 3 + 8, 83 = 10 x 8 + 3

   Add the two sums, e.g. 38 + 83 = 121
   Divide the answer by 11, e.g. 121 ÷ 11 = 11
   The result is always the sum of the two digits, e.g. 3 = 8 = 11.
   Does this always happen? Why?

   Hint: If b is the first digit and r is the second digit, then a model of 10b + r looks like this. 
   What will the model of 10r + b look like?

   
   Why will the sum of 10b + r and 10r + b equal 11 x (b + r)?

Session 1

In this session we use paper strips to help us solve fraction problems.

1. Use Copymaster 1 to produce paper strips with various divisions across the bottom. Enlarge the copy to A3 size so the strips are easier to handle. Be sure that students cut the strips around the exact outside, and do not leave extra length. Introduce the activity by saying that a new company is producing fruit strips with cutting marks. This modification is to make equal sharing of the strips between friends much easier. You might use another context instead such as making a tuke (cubit) long measurement stick or dividing an eel up to share it among whānau members. Here is a 12-mark strip. Ask, "How could these marks be used to find half of the strip?"
    
2. Students should suggest that folding would be easy and that the fold mark will line up with the 6. Draw this action as a double number line like the one below. Use a paper strip to draw the number line so all numbers are located correctly to scale.
   
    
3. Ask: What other fractions are easy to fold with this strip?
   Students should suggest quarters, thirds and possibly sixths. Use their responses as an opportunity to add fractions to the number line. Include unit (denominator of 1) and non-unit fractions, like three quarters. For example:
   
    
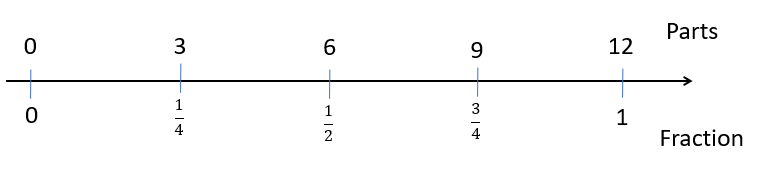
4. Write the equation for the halving problem as 1/2 x 12 = 6. Explain that the equation means “One half of 12 equals 6.”
    
5. Ask students to record how the other fractions of 12 might be written as equations. For example, 3/4 x 12 = 9 and 2/3 x 12 = 8.
    
6. Ask students to use the 15 parts strip.
   What fractions would be easy to fold with this strip? Why would those fractions be easy?
   Students might suggest that thirds and fifths are easy because 15 divides equally by 3 and 5. Ask them to work in pairs, folding one strip into thirds and one into fifths.
    
7. Ask students to work together to create a number line that includes thirds and fifths, including the fractions with more than one as the numerator (non-unit fractions).
   
    
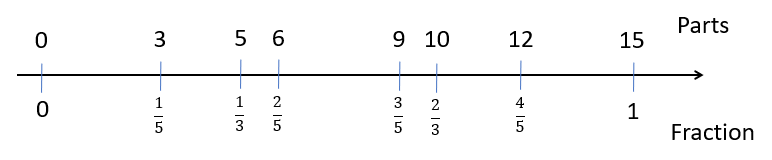
8. Draw students’ attention to important features of the number line with questions like:
   Where would the fractions 3/3 (three thirds) and 5/5 (five fifths) go? (These are equivalent fractions for one, just like 2/2 and 4/4)
   How would you find one half of this strip? How many thirds and fifths are equal to one half? Folding in half yields 1 ½ / 3 (one and one half thirds) and 2 ½ / 5 (two and one half fifths).
   Are the thirds in the same position on this number line, with 15 parts, and on the previous number line with 12 parts? Why does that happen? (Since both strips were the same length, the same fractions align).
    
9. Ask students to record some fraction multiplication problems for the 15 part strip. For example, 2/3 x 15 = 10 (two thirds of 15 equals 10).
    
10. Share the equations. Ask students to justify their equations using the strip model. Does a student record, 1/2 x 15 = 7 ½?
     
11. Set the students a few closed problems to solve using the fruit (paper) strips:
    • 1/3 x 24 = ?
    • 2/5 x 15 = ?
    • 2/3 x 18 = ?
    • 1/2 x 28 = ?
    • 4/10 x 30 = ?
    • 2/5 x 25 = ?
       
12. Open up the task so it is group worthy.
    Choose a strip we have not used as a class. Use that strip to create a number line with at least six different fractions.
    or
    Create a fruit strip that can be folded into many different fractions, using the lines. 
    What number of parts is a good choice? Why?
     
13. After a suitable time, discuss students' attempts. You might staple the strips that groups create on the wall, vertically aligned.
     
14. Eyeball some fractions and record them:
    Which fraction is greater in this trio; 2/5, 4/10, 1/5? How do you know?
    The discussion might provoke the concept of equivalent fractions, and help students to realise that the size of a fraction is determined by the size of both the numerator and denominator.
     
15. Tell the students that an employee at the fruit strip company invented the 17 part strip or use the measurement stick or eel scenario. His boss is not convinced that the 17 part strip is useful. Is the boss correct? (Seventeen is a prime number so the only fraction the strip can be divided evenly into is seventeenths).

Session 2

1. In this session students solve fraction problems using division. The variation in this session is that the whole set is variable. This provides a contrast to session one in which the whole strip length was kept constant. Students also build on the concept of fractions within ratios.
    
2. Tell the students that they are working for the company that makes endless pencils. These pencils have a variety of leads that can be pushed through the body of the pencil until the required colour is found. Tell six students to make each make a pencil containing three yellow leads and one blue lead. The students make a stack of coloured cubes to represent each pencil. Put the "endless pencils" into a cardboard packet (e.g. a Milo Box).
    
3. Ask: What fraction of the leads (cubes) in this box are yellow? (three-quarters).
   Do students realise that each unit of four pencil leads is three quarters yellow so the whole set must be three quarters yellow?
   There are 24 leads altogether. How many of them are yellow?"
    
4. Allow the students time to attempt the problem and then discuss their strategies. Some may derive the result from one-half, "One-half would be 12, so one-quarter is 6, so three-quarters is 18." Others may use a division strategy; "I knew that there are six pens. There are three yellow leads in each pen so that is six times three, that’s eighteen." Remind the students that what they have solved could be represented as an equation, as a double number line, and as a ratio table, as shown below:
   • Equation: 3/4 x 24 = 18.
   • Double number line:
     

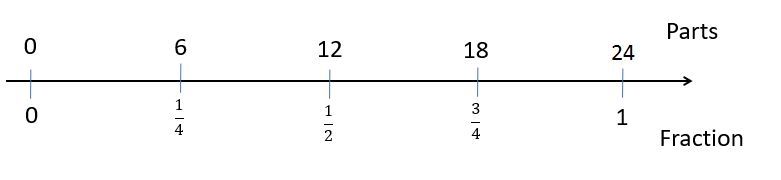
   • Ratio table:

     Number of parts	24	6	12	18
     Fraction	1	1/4	1/2	3/4

     
      

5. Prepare other examples of packets of endless pencils.
   • Eight pencils (stacks of cubes), each with two red and three black leads (box labeled: 40 leads. Two red and three black are in each pencil. How many black leads are there altogether?")
   • Six pencils, each with two green and one yellow leads (box labeled: "18 leads. Two green and one yellow are in each pencil. How many green leads are there altogether?")
   • Seven pencils, each with five blue and three red leads (box labeled:"56 leads. Five blue and three red are in each pencil. How many blue leads are there altogether?")
   • Ten pencils, each with three blue and seven white leads (box labeled:"100 leads. Three blue and seven white are in each pencil. How many blue leads are there altogether?")
      
6. With each packet take two pencils out to show the students the kind of pencil inside. Encourage students to use whatever strategy they think is appropriate to solve each problem. Use equations, double number lines, and ratio tables to record the strategies as they are reported back.
   For example, problem ii) might be solve like this:
   • Equation: 2/3 x 18 = 12 or 4/6 x 18 = 12
   • Double number line:
     

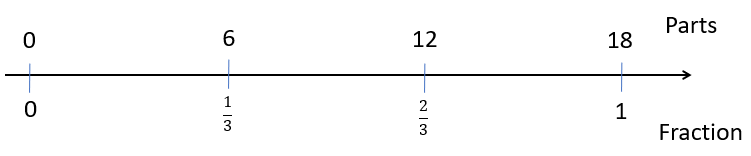
   • Ratio table:

     Number of Parts	18	1/3	2/3
     Fraction	1	6	12

     
      

7. Provide packets, labels, and cubes so that groups of students can make up similar pencil problems for other groups to solve. The problems can be exchanged. Ask the solver group to discuss their solutions with the creator group.
    
8. Conduct a plenary for your students where you share important connections among ways to represent fractions. Highlight these points:
   • The pencil shown below has a ratio of 2 grey leads to 3 white leads.
     
   • The relationship of colours can be written as a ratio 2:3 and as fractions 2/5 grey and 3/5 white.
     Why are the fractions fifths?
   • If the ratio is copied this results in a range of pencils that all have the same fraction of grey and white. For example, the ratio below is 6:9 (three copies of 2:3).
     
   • The longer pencil is still 2/5 grey and 3/5 white though the fractions could be expressed as 6/15 and 9/15.
   • The number of grey leads could be worked out using 2/5 x 15 = 6.
     How could the number of white leads be worked out in this way?
     
     The operation involves 15 ÷ 5 = 3 to find one fifth of 15, then 2 x 3 = 6 to find two fifths of 15.
     How could the number of white leads be worked out in this way?
      
9. Pose similar practice problems for your students.

Session 3

1. In this session students transfer their knowledge of fractions to create tenths, hundredths, thousandths and ten-thousandths. In doing so, they connect fraction and decimal notation.
    
2. Write 4 567 on the board and ask the students to tell you what they know about the number. Some will mention the place values (thousands, hundreds, tens, ones). Ask what the next place value is to the left is and how they know that (ten thousands because that is ten times the place immediately to its right). Ask what the place to the right of the ones place is. Some students may know that the place is the tenths but encourage them to justify if (division by ten with each next place to the right). 
    
3. Make some stacks of connecting cubes that have one yellow and one red cube (a model for halves). 
   What fraction of the stacks are yellow? (one half).
   In order to express one-half as a decimal we need to find an equivalent fraction for it that is so many tenths.
   How can we show one-half as tenths?
   Students might know that five stacks will show one-half as five-tenths. If this knowledge has not yet been developed, spend some time using Deci-cubes, number lines, or another appropriate material to reinforce the relationship between one-half and five-tenths. How do we write one-half as a decimal?
   Most students will know that the decimal for one half equals 0.5 but will not recognise the connection to tenths. Record the decimal as:
    
    
4. Ask several students to produce stacks of cubes that have one blue to four white.
   What fractions are in this ratio? (Students should say one fifth and four fifths)
   Could we copy this ratio until we have tenths? (two copies will make a collection ten cubes)
   How many cubes will be blue and how many will be white?
   What are the decimals for one fifth and four fifths? (0.2 and 0.8)
   What are the decimals for two fifths and three fifths? (0.4 and 0.6)
    
5. Show how the fractions of fifths can be expressed as decimals by counting in lots of two tenths on the place value chart.
   
    
6. Follow a similar process with quarters. Ask all students in your class to make stacks of one black cube and three white cubes. 
   Can the ratio be repeated until there are ten parts, tenths? (No)
   What is the decimal place to the right of the tenths? (Students may notice the symmetry about the ones place or realise that dividing ten parts each into ten parts give hundredths)
   Can the ratio be repeated until there are one hundred parts, hundredths? (Yes)
   How many copies of 1:3 are needed? (25)
   How many of the 100 cubes will be black? (25/100) How many will be white? (75/100)
   What are the decimals for one quarter, and three quarters? (0.25 and 0.75)
   
    
7. You might show why the fractions are expressed as tenths and hundredths. Repackaging 25 black tubes into two towers of ten and five cubes shows how the notation works. Each tower is one tenth of the total collection of 100 cubes. Do the same thing with the white cubes to form seven towers of ten (7 tenths) and five cubes (hundredths).
   What is the decimal for two quarters? Why? (Students will know that two quarters equal one half and the decimal for one half equals 0.5)
   If one quarter equals 0.25, then two quarters equals 0.50. Why is two quarters shown as 0.5? (A calculator will discard unneeded zeros)
    
8. Tell the students that you are going to give them some commonly used ratios. Their task is to identify the fractions within the ratios and work out the decimal for each fraction. They may use cubes, number lines, and place value tables but they may not use a calculator. Write up the following ratios:
   • 1 red cube: 9 blue cubes (one tenth: nine tenths)
   • 4 green cubes: 6 yellow cubes (four tenths: six tenths)
   • 3 black cubes: 5 orange cubes (three eighths: five eighths)
   • 6 red cubes: 2 blue cubes (six eighths: two eighths)
   • 2 white cubes: 1 green cube (two thirds: one third)
      
9. After a suitable period of investigation, discuss their answers. Important points to bring out are:
   • The decimal place to the right of the hundredths is the thousandths place.
   • As the places include more parts it is easiest to use multiplication to figure out the decimals, e.g. 125 copies of eight cubes make 1000.
   • Equivalent fractions have the same decimals, e.g. 6/8 = ¾ = 0.75.
   • Decimals for some fractions have recurring digits and do not terminate, e.g. 1/3 = 0.3333….

Session 4

In this session we use calculators to explore the links between fractions and their decimal equivalents. 

1. Many students will know that calculators can be used to convert fractions into their decimal equivalents. Model this with some well-known fractions such as 1/2, 1/4, 2/5 and 3/8.
   The decimal for one-half can be found by entering 1 ÷ 2 = . 
   Why does the operation one divided by two give the answer of one half, 0.5?
   If one anything is partitioned equally into two parts, one of those parts equals one half.
   The decimal for one-quarter can be found by entering 1 ÷ 4 = 
    
2. Ask: How can the decimal for three quarters be found?
   The decimal for three-quarters can be found by entering 1 ÷ 4 = then multiplying the answer by three (3/4 is three lots of one quarter). Alternatively, use the operation 3 ÷ 4 = 0.75.
    
3. Tell the students that you are now going to go the other way round and give them some decimals. Their job is to find the equivalent fractions. that these decimals represent. Add that they may use any of the strategies used in the previous session, like the double number line, ratio table, or cube model.
    
4. Write up the following decimals for them to explore:
   0.6;       0.8,    0.3,    0.7,   0.75;    1.5;       1.25 (five quarters);     0.325 (three eighths);   0.875 (seven eighths);   0.6666….(two thirds);    1.2 (six fifths or 12 tenths);       0.8 (four fifths or eight tenths) , 0.4444….  (four ninths);  0.3125 (five sixteenths)
    
5. Allow the students to work in pairs and to discuss their findings. It is important that they record their answers.
    
6. After a suitable period of investigation, bring the class together to discuss their strategies. Encourage tuakana-teina by prompting more knowledgeable students to share their thinking with the whole class, or in small groups. Key ideas will be:
   • Use of known fraction-decimal links to get at unknowns, e.g. 1/5 = 0.2 and 1/10 = 0.1 so 0.6 = 3/5 or 6/10
   • Recognise that when a decimal is greater than one the corresponding fraction is improper, that is its top number (numerator) is greater than its bottom number (denominator).
   • Recurring decimals (decimals where a section of the numbers repeat) indicates a fraction that cannot be expressed as an exact number of tenths, hundredths, thousandths, etc.
      
7. If students experience difficulty with some decimals, suggest the use of scaffolding strategies. For example, when nothing in the decimal looks familiar explore the unit fractions until a useful decimal is found. In the case of 0.4444… finding that one ninth (1 ÷ 9 = ) 0.1111… is handy. Four lots of one ninth equals four ninths, 4 ÷ 9 = 0.4444…
    
8. Use a double number line progression to find the fraction for a recurring decimal:
   
    
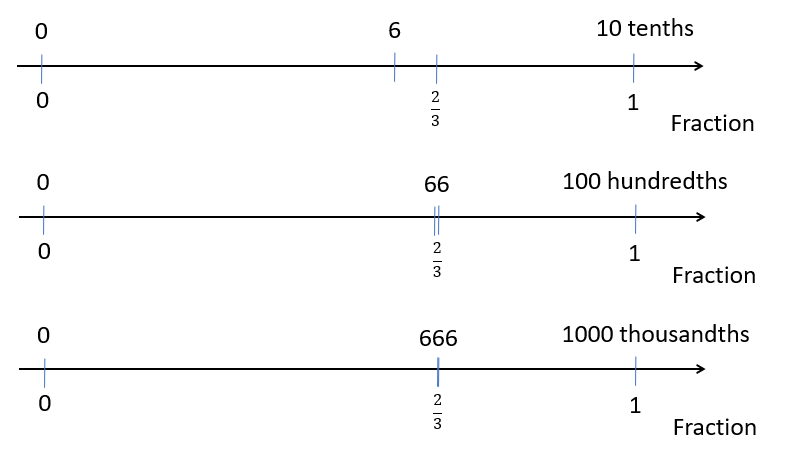
9. Successive progressions make it easier to estimate the fraction accurately. In this case knowing one thirds equals about 33/100, so two thirds equals about 66/100. The fraction can be confirmed using mental calculation or the calculator, and altered to become more accurate, e.g. 333/1000 is closer to one third than 33/100.
   
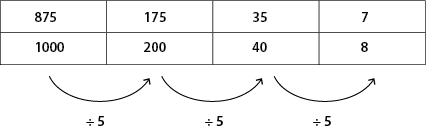
   Similarly a ratio table might be used to reduce a decimal to its simplest fractional form. For example, 0.875 by knowing this fraction equals 875/100.
   

Session 5

In this session students apply their knowledge of fractions, and their decimal equivalents, to solve problems involving litres and millilitres. The metric system is based on decimals, since it uses a base of ten.

1. Ask the students to bring along 1 litre empty plastic drink bottles. Fruit juice often comes in 1 litre bottles which is preferable to 1L milk bottles that are not as regular. Ensure that a solid mark is shown on each bottle at the 1 litre point. Give students access to a set of measurement jugs so they mark accurately. Discuss the relationship between litres and millilitres. The litre is the base unit of capacity and is equivalent to the volume of a cube that measures 10cm x 10cm x 10cm (large place value block cube). Milli is the prefix for 1/1000 (one thousandth) so a millilitre is one thousandth of one litre. This relationship can be written as 1mL = 0.001L, or 1000mL = 1L.
    
2. You might create an imaginary story for the task, such as the bottle being the emergency water supply that needs to be managed as they cross the desert or the ocean. Consider how this story can reflect the cultural make-up and interests of your class (e.g. when learning about the legend of Matariki and the six sisters, the bottle could represent the water collected by Ranginui to nourish the plants, animals and people). Tell the students that they will be given two 1 litre bottles, several rubber bands (to mark water levels), a marker, and a measurement jug. Their task is to mark one of the bottles to show where the water level would be if it was one-half full, one-quarter and three-quarters full, one-eighth, three-eighths, five-eighths, and seven-eighths full. Ask your students to use fraction symbols to make the marks, e.g. 3/8. 
    
3. Put the students in mixed achievement groups to solve the problem. Watch your students and look for the following:
   • Do they recognise that decimals, thousandths can be used to accurately find the marks?
   • Do they show understanding of tenth, hundredths, and thousandths?
   • Do they label the marks appropriately with fractions (and possibly decimals)?
      
4. After a suitable period of exploration, bring the class together to share their strategies. Some students may have used pouring methods to find the marks. For example, half can be found by splitting a full bottle equally between two bottles, one quarter can be found by splitting one half between two bottles, etc. Other students may have used the decimal properties of the metric measurement system. For example, to find the three eighths mark, they may realise that its decimal is 0.375 and so measure out 375 millilitres using the measurement jugs (Since there are 1000 ml in 1 litre).
    
5. Ask how it might be possible to find the one-third and two-third marks if they had another bottle. Get them to predict approximately where these marks will be. Students should use their knowledge of ordering fractions to do this. For example, two-thirds is slightly more than five-eighths since 0.6666... is more than 0.625.
    
6. Get the students to find the one-third and two-third marks by pouring between 1 litre containers rather than measuring. They might fill one container to the 1L mark, then share the contents equally among three same shaped containers (large plastic glasses are good for this task). Pouring one then two third shares into the original container gives the one third and two thirds marks. Then get them to check the accuracy of their pouring using measurement. One-third of a litre is about 333 millilitres. Recognise that students will not usually achieve that degree of accuracy by pouring.
    
7. Extend the activity be asking for other fraction marks:
   • Tenths are lots of 100mL (0.1L)
   • Fifths are collections of two tenths (0.2L)
   • Sixths are halves of thirds (0.1666…L)
   • Ninths are thirds of thirds (0.1111…L)
      
8. Optional. Extend the task using a large plastic refill bottle from a water cooler. These bottles vary in size and might be 12, 15 or 20 litres. Pose problems like:
   • If the bottle is two thirds full, how many litres of water are left?
   • If the bottle is a fraction fill, how many litres of water are left?

Getting started

1. Show the students PowerPoint 1. The first slide shows a football made of pentagons and hexagons. You could add pictures of buildings from your local community that show polyhedra in real-world contexts to this PowerPoint.
   What do you know about this solid shape?
2. Ask students to attend to the shapes that make the solid.
   What shapes can you see? (Pentagons and hexagons)
   Look at the vertices (corners). How many of each shape meet at one vertex? Is that combination the same for each vertex? (Two hexagons and one pentagon meet at each vertex.)

3. Slide two shows a cube. Show students a cube you have constructed from plastic polygons (polydrons, geoshapes, etc.) or card (see below).

   What is this solid shape called? (a cube)
   What shapes is it made from? (squares)
   How many of those shapes are needed? (six)
   How can you count the faces to check you count them all?  (e.g. top and bottom, four faces around the middle.)

4. Explain that the corners can be called vertices.
   How many vertices does a cube have? (eight) 
   How did you count them?
   ​How many edges does a cube have? (12)

5. Pose this challenge:
   How many different solids can you make only using equilateral triangles or squares? Let's try to build solids that look balanced. 
   If needed, go back to the example of the soccer ball to provide an example of symmetric balanced solid.

   Allow the students time to build the solids. After a suitable collection has developed, bring the class together. Look for the tetrahedron and octahedron.
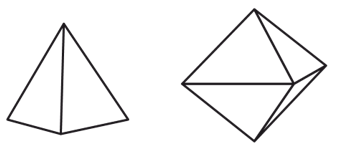
   What is the same about these two solids? (made only of triangles)
   
   The solid on the left is called a tetrahedron. What does tetra- means? (four)
   The solid on the right is called an octahedron. What does octa- mean? (eight)

6. Point out that regular polyhedra are named by the number of faces.
   Does anyone have a different polyhedron made only from triangles?
   If a student has created an icosahedron (icosa- means twenty), draw the student's attention to it. If not, show slide four of PowerPoint 1.

   

   Look carefully at each vertex of the three polyhedra we have made from triangles.
   What do you notice?
    

7. Focus the discussion on the consistent pattern around each vertex. Three triangles surround each vertex of the tetrahedron, four triangles for the octahedron and five for the icosahedron.
    

8. Is it possible to put six triangles around each vertex and make a solid? 
   Have students try to see if it works.

   Surrounding a vertex with six triangles creates a tessellation which covers a plane, or flat surface. The internal angles of an equilateral triangle all measure 60°. Six angles of 60° add to 360° which is a full turn and is "flat" when joined. Therefore it isn't possible to make a solid with six equilateral triangles at each vertex. 
    

9. One of the students is likely to have made this polyhedra called a triangular dipyramid (made of two triangular based pyramids). 

       

   This solid does not belong with these (tetra-, octa- and icosa-). Why not?
   If you count the number of triangles surrounding each vertex, what do you get?

   Some vertices have four triangles meeting (around the ‘equator’) and some have three triangles meeting (top and bottom). There is not the same number meeting at every vertex which is a requirement for Platonic solids.
    

   1. Other students are likely to have made these solids.

      
       

      Square based pyramid

      Cuboctahedron

      Rhombicuboctahedron

      Draw your students’ attention to the configuration of polygons around each vertex. For the square based pyramid the apex has four triangles around it and each base vertex has a square and two triangles. A square based pyramid might be excluded from the set of balanced symmetrical solids because it is not balanced if it is sitting on one of its triangular sides. For the cuboctahedron there are two squares and two triangles around each vertex. For the rhombicuboctahedron there is one square and three triangles around each vertex.

10. For all of the balanced symmetric solids made from triangles and squares, ask your students to work out how many faces each solid has. For the tetra-, octa- and icosahedron the prefix names the polyhedron. However, counting the faces on the cuboctahedron and rhombicuboctahedron is a bit more challenging. Encourage your students to record their data systematically:

    Solid	Number and shape of faces	Numbers of vertices	Number of edges
    Tetrahedron	4 triangles
    Octahedron	8 triangles
    Icosahedron	20 triangles
    Triangular dipyramid	6 triangles
    Cuboctahedron	8 triangles 6 squares
    Rhombicuboctahedron	8 triangles 18 squares

11. Look for systematic ways to count the number of faces. That might include sectioning off the solid into parts or methodically accounting for each vertex.

Session Two

1. Remind the students that in the previous session they were only allowed to use triangles and squares.
   What solids did we make?
   As the students remember it, bring out a model of the solid and name it.

2. Explain that there is a special group of polyhedra called Platonic solids, that were found by the ancient Greeks. Explain that there are two criteria for a Platonic solid:

   • The faces of the solid are all identical, regular polygons. 
   • The same number of faces meet at each vertex.

   
   Note that regular means that the sides, therefore the angles, of the polygon are the same. Use chalk on the floor to draw this Carroll diagram and place the models within it. This is a complex classification, so you may need to support students to do it.

   	Each vertex is the same	The vertices vary
   One regular shape
   More than one shape

   The solids in the top left quadrant are perfect, the others are not.  

   What other shapes have you got in your set?
   Can any other perfect solids be made with the other shapes?

3. Let the students explore the possibility of other perfect solids. Only one more exists, the dodecahedron (dodeca- is the prefix for twelve).
   
    

4. Students might have found that hexagons do not work.
   Why can you not make a perfect solid with hexagons?
   At least three polygons are needed around a vertex. The internal angles of a hexagon measure 120°. Three lots of 120° totals 360° which is a full turn. Therefore, no angle is unfilled for the polygons to come off the flat as the sides are joined.

    
    

5. Add the dodecahedron to the set of perfect solids. Include it in the table along with the other data.
6. Start with the tetrahedron which is the simplest Platonic solid. Hold up the model of this solid.
   Imagine if I unpeel the tetrahedron and lay it flat. That pattern is called a net.
   What do you think it will look like?
   Ask your students to sketch their predictions for the net. They can check their predictions by making each net and folding it up to check.
   There are two possible nets:
        
   There is also an arrangement of triangles that does not work.
   
   Why do the two top nets work but the bottom one does not?
   The reasons why a net will not work are sometimes as important as the reasons why a net will work. All of the nets have four equilateral triangles. This is an essential condition. Nets that fold to make a tetrahedron allow only three corners of a triangle around each vertex when they fold. The bottom allows for four corners around the central vertex, so will not fold to make a tetrahedron.
7. Ask the students to investigate:
   How many different nets will there be for a cube?
   Provide each pair of students with square grid paper and six square polydrons. Allow lots of time for the students to find and record possible nets.

Session Three

In this session students try to find a solution set for all the nets of a cube.

1. Challenge students to work in pairs to find all the possible nets for a cube.
   How many different nets can you make that will fold to make a cube?
2. Once students have drawn several nets, invite a few students to share their favourite net. Begin a gallery of possible nets. An important issue is how to establish that two nets are different. You might use an example like this:
   
   Are these nets the same or different?
   Students might notice that one net can be mapped onto the other by reflection or rotation, or both in this case. That means that the nets are not unique (different in a mathematical sense).
3. Remind the students that you are seeking a full set of nets.
   Has anyone got a system for finding all of the nets?
4. Some students may have noted a family of nets that have four squares in a row. The central line of four can be kept constant and the other two faces moved around to form unique nets. Here are three ‘four in a row’ nets. There are six such nets.
   
   A provoking question might be:
   Is it possible to make a net that has no more than three squares in a row?
   What about only two squares in a row?
5. Let the students continue to explore possible nets until they think they have found them all. Can they justify that those nets are the full set?

6. Gather the class and add to the gallery by asking students to come up with a ‘new’ net. Check each offering is not a reflected or rotated copy of another net. Polydron models are helpful for this as they can be turned and flipped to map onto each other.

    

7. In total there are 11 nets. Carefully organising the nets can help students see a common structure in families of nets. For example, here are the four squares in a row family.
    
   Note that the top four nets fix the top-left square and move the right-hand square to different positions. The next two nets fix the left square to the second central square and find two new positions for the right square. The top-right and bottom-right positions have already been covered in the first four nets.
   Another four nets can be found by organising three squares in a row and manipulating the other three.
   
   The final net has no more than two squares in a row.
   
    
8. Look for your students to check any new nets for uniqueness, which means the new net does not map onto an existing net by reflection and/or rotation. For example, in this work sample William signals that a new net is the same as a previous net by bracketing the net.
   
    
9. Your students might like to attempt finding nets for the other three Platonic solids. Encourage them to sketch the net for the solid they choose on grid paper. They can check the accuracy of their net by making it with polydrons and folding.
10. Do your students:
    Use symmetry to form the net?
    Divide the solid into two halves to simplify the task?
    Fix one face as the base or top and imagine the other faces connected to it?
    Image the folding of faces to locate them correctly?

Session Four

1. Show your students PowerPoint 2. Slide One shows three different views of an octahedron. Ask them to sketch the different views by drawing only the edges and vertices they can see, and not drawing those that are hidden. Slide Two has simple drawings of the same views. Not drawing what they cannot see is a challenge for some students. Asking them to imagine what a digital camera will ‘see’ then create the drawing is a good strategy. Comparing the drawing with the digital camera image helps your students attend to the features that are actually captured.
2. Ask your students to take one of the solids they have made and draw three different views of it. The more complex solids like the icosahedron and rhombicuboctahedron can be quite challenging to draw but the simpler solids are very accessible.
   For example, the cube (hexahedron) has many possible views.
   
    
3. Once students have created views of their chosen solid they can give the views to a partner who tries to image what perspective the solid was drawn from.
4. It is interesting to discuss how perspective changes the way shapes appear. In the views of a cube above a square appears as a non-square rectangle and a rhombus. A square can also appear as a trapezium from certain angles. Learning about perspective drawing in visual art could complement the learning in this session.

Session Five

In this session students create accurate nets for two families of polyhedral, called prisms and pyramids. They look for properties in the nets and consider the relative lengths of edges/sides.

1. Show the students PowerPoint 3. Slide One has three examples of prisms.
   How are these solids the same and how are they different?
   Students should notice how all three solids have rectangular faces though the end faces are different (triangle, square and hexagon). Tell the students that the solids are examples of prisms, polyhedra with consistent cross section. Imagine that each solid was a loaf of bread. It is possible to slice the solid into pieces of the same shape.
   Each prism is known by its cross section. For example, a triangular prism has triangular cross sections.
    
2. Ask your students to imagine the net for a rectangular prism. Ask them to sketch the shape of it in the air. Focus on the shapes that must be in the net and relate those shapes to the picture on Slide One. Four rectangles must wrap the end faces which are squares. Give the students 1cm square grid paper. The squares are useful for maintaining right angles and measuring lengths.
    
3. Ask students to use a ruler and pencil to create an accurate net for a cuboid. An accurate net must fold so the sides meet exactly to become edges. Students can check their nets by cutting them out and folding. A common issue for students is that sides in the net that meet to form edges must be congruent (same length).
   
    
4. Once the net for a rectangular prism is established, focus on the triangular and hexagonal prisms.
   What will need to change in the net to form a triangular or hexagonal prism?
   Do students recognise that the end faces will need to be triangles or hexagons and that the number of rectangles must match the number of sides? For example, a triangular prism will have only three rectangles. Invite your students to create nets for other kinds of prisms. The grid paper will still be useful though the challenge of getting the matching sides is more difficult.
    
5. Watch to see how your students create triangles and hexagons that have the same side length as the short side of the rectangle.
    
6. Bring the students together to share their nets.
   What is the same with all of the nets?
   What are the differences?
   Imagine the net for an octagonal prism. What would it look like?
    

7. You could create a table of data about the prisms and look for patterns, or you may choose to keep the lesson focused on nets.

   Prism	Number of faces	Number of edges	Number of vertices
   triangular	5	9	6
   rectangular	6	12	8
   hexagonal	8	18	12
   Octagonal	10	24	16

8. Alternatively, move to Slide Two of PowerPoint Three to discuss the common features of the solids. All of the pictures show pyramids. The base of the pyramid names it. For example, a square based pyramid has a square base. Begin with the square based pyramid.
   What shapes are in the net of this solid?
   How do you know there will be four triangles?
    
9. Ask students to sketch their prediction for the net.
   Which sides will need to be the same length?
   
    

10. Students can make an accurate net for the square based pyramid or try the challenge of the more difficult pyramidal nets. The net for an octagonal pyramid is an excellent mid-level challenge. As with the prisms you might create a table of data and look for patterns.

    Pyramid	Number of faces	Number of edges	Number of vertices
    Triangular based	4	6	4
    Square based	5	8	5
    Hexagonal based	7	14	7
    Octagonal based	9	18	9