Students will need to understand the following:

• A face is a flat surface.
• An edge is where two faces meet.
• A vertex or corner is where edges meet.
  
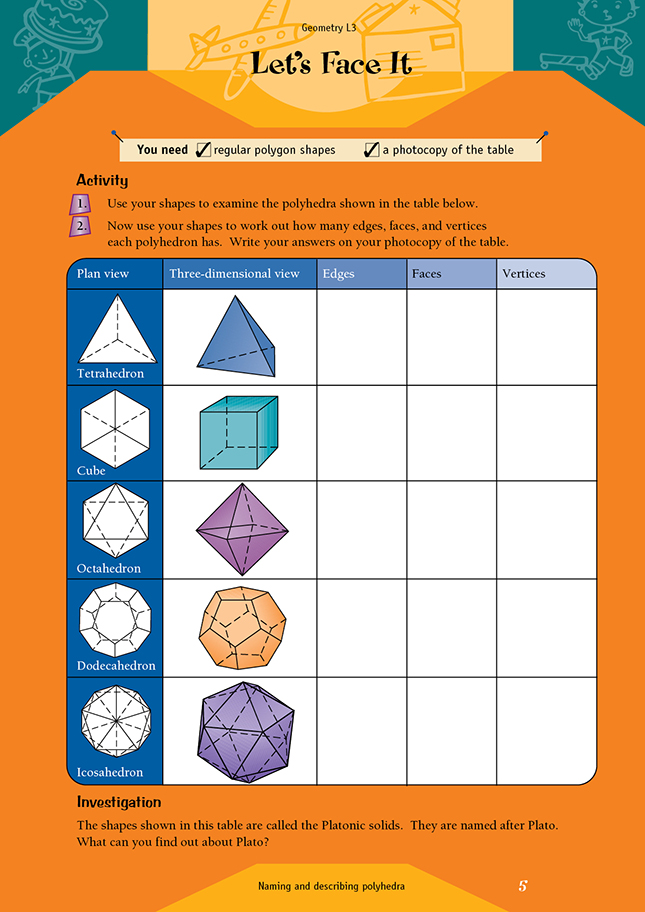
• A polyhedron is a solid shape with flat sides. A solid shape has three dimensions – length, width, and depth. The faces of a polyhedron are all polygons.

You could begin by making the cube and discussing with students the properties of the cube, especially the polygons that make up the faces and the number of faces, edges, and vertices.
Encourage students to look for polyhedra in everyday shapes found in the environment. You may find the following definitions useful:

• A tetrahedron or triangular pyramid is a solid with four triangular faces. It is the same as a triangular-based pyramid.
• A cube is a regular solid with all its faces square and all its edges equal in length. Most dice are cubes.
• An octahedron is a solid shape with eight faces. In a regular octahedron, each face is an equilateral triangle.
• A dodecahedron is a solid shape with 12 faces. All the faces of a regular dodecahedron are regular pentagons.
• An icosahedron is a solid with 20 faces. In a regular icosahedron, each face is an equilateral triangle.
  

An interesting extension and discussion point is Euler’s formula: faces plus vertices minus two will equal the number of edges (F + V – 2 = E). (Euler [1707–1783] was a Swiss mathematician who produced a number of important mathematical works and hundreds of mathematical and scientific memoirs.) If we use an icosahedron as an example of Euler’s formula, 20 + 12 – 2 = 30.
An icosahedron has 30 edges.
A useful question could be: “If I added the number of faces and vertices together, what do I need to do to get the same number of edges as shown in the table? Does Euler’s formula always work?” This formula introduces some algebra and links to the achievement objective: describe in words,
rules for continuing number and spatial sequential patterns, Algebra, level 3.

Investigation

The cube, tetrahedron, octahedron, dodecahedron, and icosahedron are known as Platonic solids. They are named after Plato (428–347 B.C.), who studied each solid intensively. Plato attributed the four main elements in the universe to the platonic solids: fire – tetrahedron, earth – cube, air – octahedron, and water – icosahedron. He also attributed the world to the dodecahedron.

Answers to Activity

1. Practical activity

2.

Investigation Research on Plato