Matariki - Level 1
This unit consists of mathematical learning, at Level 1 of the New Zealand Curriculum, focused around celebrations of Matariki, the Māori New Year. The sessions provide meaningful contexts that highlight Māori culture and provide powerful learning opportunities that connect different strands of mathematics.
- Assemble parts of a shape to form the whole.
- Create symmetrical figures (reflection and rotation).
- Calculate the number of direct ancestors they have.
- Use fractions to create rhythmic percussion patterns.
- Order events.
- Describe the likelihood of outcomes using the language of chance.
- Measures quantities to follow a recipe.
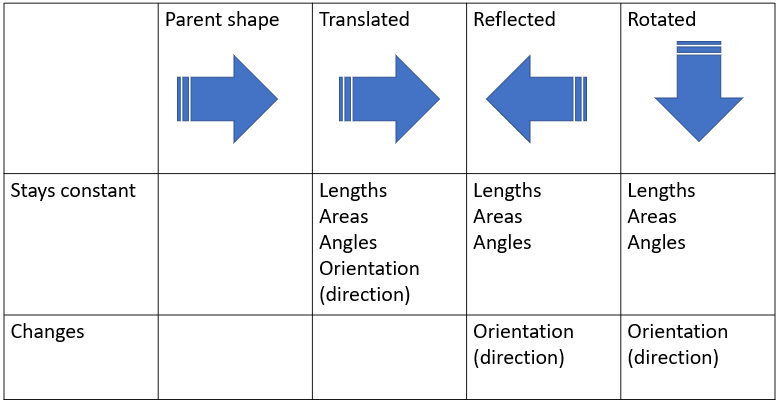
In this unit the students will apply different mathematical and statistical ideas, such as the properties of symmetry. In this, they will demonstrate understanding of the features of a shape that change and remain invariant under translation, reflection and rotation.
Students also apply simple probability. For example, given this set of cards, what is the chance of getting a bright star if you choose one card at random? Random means that each card has the same chance of selection.

The set of all possible outcomes contains four possibilities. Two of those possible outcomes are selecting a bright star card. The chances of getting a bright star are two out of four or one half. There is a one quarter chance of getting a fuzzy star and the same chance of getting a rainy cloud.
The learning opportunities in this unit can be differentiated by providing or removing support to students, or by varying the task requirements. Ways to support students include:
- explicitly modelling the key mathematical processes that students are required to apply in each session (e.g. measuring, identifying fractions)
- supporting the use of specific counting and addition and subtraction strategies in reflection of your students’ strengths and strategy knowledge
- modifying the numbers utilised in each session to suit the needs of your students
- grouping students to encourage tuakana-teina (peer learning) and mahi-tahi (collaboration).
Although the context of Matariki should be engaging, and relevant, for the majority of your learners, it may be appropriate to frame the learning in these sessions around another significant time of year (e.g. Chinese New Year, Samoan language week). This context offers opportunities to make links between home and school. Consider asking family and community members to help with the different lessons. For example, members of your local marae may be able to share local stories and traditions of Matariki with your class.
Te reo Māori language is embedded throughout this unit. Relevant mathematical vocabulary that could be introduced in this unit and used throughout other learning include āhua (shape), shape names (e.g. whetū - star), hangarite (symmetry, symmetrical), whakaata (reflect, reflection), huri (rotate, rotation), tātai (calculate, calculation), tāpiri (add, addition), hautau (fraction), raupapa (sequence, order), tūponotanga (chance, probability), and ine (measure).
- Pattern blocks or access to internet for students
- Mirrors
- Ingredients and baking equipment for making rēwena bread (see Lesson Five)
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- PowerPoint 1
- PowerPoint 2
- PowerPoint 3
- PowerPoint 4
Lesson One
- Introduce Matariki, The Māori New Year, to your class. There are many picture books and online videos that could be used to introduce this context. Matariki begins with the rising of the Matariki star cluster, (Pleiades in Greek), in late May or June. For the previous three months the Matariki cluster is below the horizon so it cannot be seen. The rising signals the turn of the seasons and sets the calendar for the rest of the year.
- Show your students the first few slides on PowerPoint 1. Discuss what stars are and how our sun is an example.
What shape is a star?
Today we are going to make some stars to display using shapes. - For each slide discuss how the left-hand star is made then built onto to form the right star. Encourage your students to use correct names for the composing shapes, such as triangle, square, hexagon, trapezium. If necessary, provide a chart of the shapes and their names for students to refer to. Using a set of virtual or hard-copy pattern blocks, support students to make the stars on slides three and four by copying the pattern. Model this for students (especially if using virtual pattern-blocks). It may also be beneficial for students to work collaboratively (mahi-tahi) during this task.
- Encourage students to use the blocks to create their own stars. Slide 6 is a blank canvas of pattern blocks. With the slide in edit rather than display mode, you can use the blocks to form other patterns.
- Copymaster 1 provides two different puzzles for your students. They cut out the pieces to form a star. Glue sticks or blue-tack can be used to fasten the parts in place.
- Other Activities with Stars
- Most star designs have mirror symmetry. That means that a mirror can be placed within the star, so the star appears complete. The reflection provides the missing half of the star. Demonstrate to your students how that works. Copymaster 2 provides four different star patterns. Give students small mirrors and ask them to find the places where a mirror can go so the whole star is seen. You could also demonstrate this on a PowerPoint, or using an online tool. An internet search for “online symmetry drawing tool” reveals a number of websites that could be used. Note that Star Four has no mirror symmetry so it is a non-example. Star Four does have rotational symmetry so it can map onto itself by rotation.
- Copymaster 2 also has half stars on page two. Ask your students to complete the whole star. Be aware that attending to symmetry is harder when the mirror line is not vertical or horizontal. Can your students attend to perpendicular (at right angle) distance from the mirror line in recreating the other half?
- Creating stars by envelopes
- The diagonals of some polygons create beautiful star patterns. The most famous pattern is the Mystic Pentagram that is created within a regular pentagon. Video 1 shows how to get started and leaves students to complete the pattern. The exercise is good for their motor skills as well as their attendance to pattern and structure. Copymaster 3 has other shapes to draw the diagonals inside. Note that a diagonal need not be to the corner directly opposite, it can also go to any corner that it does not share a side with.
- Nice questions to ask are:
How do you know that you have got all the diagonals? (Students might notice that the same number of diagonals come from each corner)
Does the star have mirror lines? How do you know?
Lesson Two
In this lesson your students explore family trees, working out the number of people in their direct whakapapa. This may be a sensitive topic for some students. Thinking about our relatives who are no longer with us, or have just arrived, is a traditional part of Matariki, the Māori New Year. According to legend, Matariki is the time when Taramainuku, captain of Te Waka O Rangi, and gatherer of souls, releases the souls of the departed from the great net. The souls ascend into the sky to become stars.
- Begin by playing a video or reading a book about Ranginui (Sky Father) and Papatuanuku (Earth Mother), the mother and father of Māori Gods.
- Ask: How many parents (matua) do you have?
That question needs to be treated sensitively but the focus is on biological parents, usually a father and mother. You might personalise the answer by telling your students the names of your mother and father. Draw a diagram like this, or use an online tool to create the diagram: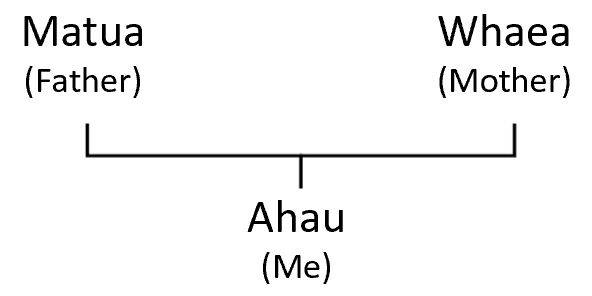
- Ask:
My mother and father had parents too. What are your parents' parents called?
How many grandparents (koroua) do you have?
Students may have different ways to establish the number of grandparents, such as just knowing, visualising the tree and counting in ones, or doubling (double two), - Extend the whakapapa tree further.
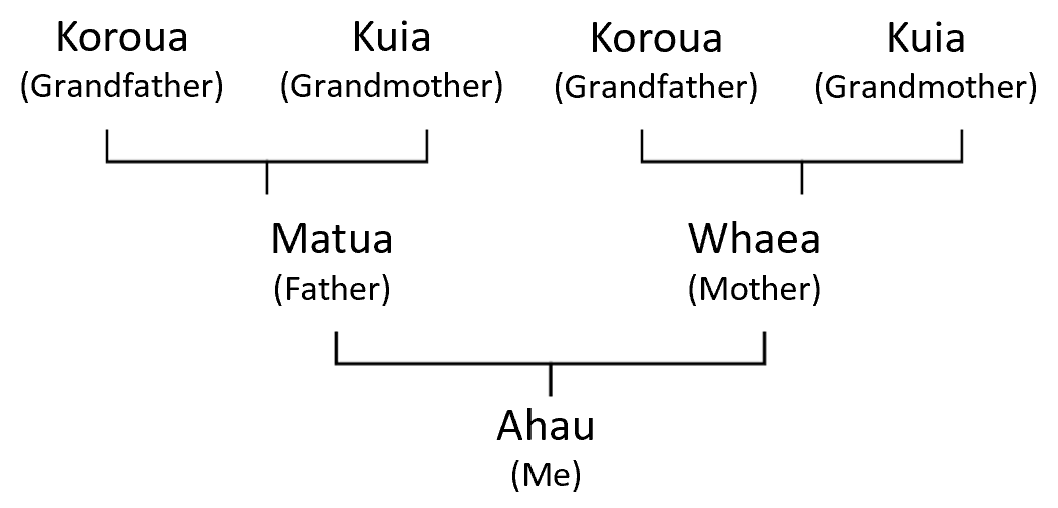
- Ask: What do we call your grandparent’s parents? (Great grandparents, koroua rangatira)
Nowadays, many students will still have living great grandparents. You might personalise the idea using your whakapapa.
What do we call the parents of your great grandparents?
Now I want you to solve this problem. How many great great grandparents do you have? - Encourage students to work in small groups. Provide materials like counters or cubes to support students. Ask students to draw the whakapapa diagram to four layers and record their strategy as much as they can. After an appropriate time, share strategies.
- Discuss the efficiency of counting based strategies, counting by ones and skip counting in twos. Highlight more efficient methods such as doubling, e.g. 2 + 2 = 4, 4 + 4 = 8, 8 + 8 = 16.
- Ask: Now let’s just think about our parents. If three children in this class invited their parents along, how many parents would that be?
Use the context as a vehicle for introducing even numbers (multiples of two), Act out three children getting their parents (other students) and bringing them to school. Change the number of students and work out the total number of parents. Find a way to highlight the numbers that come up, such as shading the numbers on a virtual Hundreds Board. - Ask: Can anyone see a pattern in the numbers of parents?
Students might notice that even numbers occur in the 0, 2, 4, 6, 8 columns of the hundreds board. - Introduce a challenge: If everyone in this class brought their parents along, how many parents would that be?
- Ask the students to work in small teams with materials. Providing transparent counters and individual Hundred Boards will be useful but provide a range of options. Watch for your students to:
- structure their model as "two parents for every one student"
- deploy materials in an organised way to represent the whole class
- use efficient counting strategies, to systematically find the number of parents
- use recording to organise their thinking, particularly the use of number symbols.
- Share the strategies students used with a focus on the points above. Depending on the current achievement of your students you might extend the problems. For example:
- Ten parents came along. How many students brought them?
- How big would our class be if 100 parents came along?
- If every student in another class brought two parents along, could there be 54 parents? What about 53 parents? Etc.
- If students in our class brought all their grandparents along, how many grandparents would that be?
- If we had to provide a Matariki celebration for our grandparents, what food and drink would we need?
- How much of each food and drink would we need?
Lesson Three
Matariki is a time for cultural activities, such as story-telling, music, and games. Titi Rakau is a traditional game that involves hitting and throwing sticks, usually to a rhythmic chant. It was used to enhance the hand-eye coordination of children and warriors. Rakau can be used as a vehicle for fractions and musical notation, as well as physical coordination. You can make the tasks below as simple or as difficult as you like.
- Look at slide 1 of PowerPoint 2.
What fractions has the bar been broken into? (Quarters)
Each of these notes (crotchet) is one quarter of a bar in this music. - Find a piece of music online with a clear 4/4 time signature. That means there are four crochet (quarter) beats to the bar. This timing is very common in popular music. “Tahi” released by Moana and the Moa Hunters in 1994 is a good example that is easily found online. Ask your students to clap in steady 1, 2, 3, 4, … time with a consistent time between claps as the music plays.
- Introduce rākau, made from rolled up magazines taped together with duct tape. Students might practise hitting the ground with the ends of the sticks on every beat of the 4/4 time. This can be changed to beat one on the ground, and beat two ‘clapping’ the sticks together in the air, beat three on the ground, and beat four in the air, etc.
- Introduce the rest symbol using slide 2 of PowerPoint Two. In 4/4 time the rest is for one beat. So the rhythm is ‘clap, clap, clap, rest, clap, clap, clap, rest…” as is used in “We will rock you,” by Queen. Slide 3 has a bar with two rests. See if the students can maintain that rhythm.
- Slides 4 and 5 introduce the quaver which is a one-eighth note in 4/4 time. See if students can manage the two different rhythms, including the beamed (joined) quavers. Copymaster 4 can be made into cards, or cut out as is, to create different rhythmic bars in 4/4 time. Note that the semibreve (circular note) denotes the whole of four beats, and the minim (stemmed hollow note) denotes one half of a bar. A minim is equivalent to two crotchets.
- Let your students make up a single bar using the cards. Encourage them to experiment with possible rhythms by trailing them with Rakau. Rests are usually part of Rakau to allow movement of the sticks from one position, e.g. floor, to another, e.g. chest. The rhythm a student creates can be played by another using Rakau.
- Look for your students to:
- Apply their knowledge of fractions, such as one half and two quarters make one whole (bar)
- Recognise equivalence, such as two quarters make one whole or two eighths make one quarter.
- Share the bar patterns that students create and play them with Rakau. Rhythms can also be checked by finding an online music composer for children and entering the notes. The software usually has playback.
- Natural extensions of the task are:
- Explore different time signatures. Many Māori action songs are in Waltz time (3/4) meaning that there are three crotchet beats to a bar. A crotchet is one third of a bar in that time signature and a quaver is one sixth of a bar.
The popular chant associated with Ti Rākau (E Papa Waiari - available on YouTube) is in 6/8 time meaning there are six quaver beats to a bar. If you watch a video of a performance with Rākau the sticks are often hit on the ground on the first and fourth beats, or clicked together on the second, third, fifth and sixth beats. - Try to work out and record the rhythm of pieces of music, using the cards. Choose a difficulty that suits your students. For example, E rere taku poi, is in 4/4 time and is the tune to “My Girl.” Kiri Te Kanawa’s recording of Te Tarahiki in 1999 features a six quaver rhythm in 3/4 time.
- Explore different time signatures. Many Māori action songs are in Waltz time (3/4) meaning that there are three crotchet beats to a bar. A crotchet is one third of a bar in that time signature and a quaver is one sixth of a bar.
Lesson Four
The rising of Matariki, in late May or June, signals to Māori that it is the start of a new year. It is appropriate for students to reflect on the passage of time. For young students there are important landmarks in the development of time, including:
- Recalling and sequencing events that occurred in their past.
- Anticipating events that might occur in the future.
- Recognising that time is independent of events, it progresses no matter what is occurring.
Cooking in a hāngī
In the first part of the lesson students work with the first two ideas, recalling the past and anticipating the future.
- Show students a video about preparing and cooking a hāngī. There are many examples online. Before viewing the video prompt your students:
Watch carefully. At the end of the video I will ask you about how to make a hāngī. - At times pause the video to discuss what might be occurring. Use the pause as an opportunity to introduce important language, like hāngī stones, kai (food), prepare, cover, serve, etc.
- Give each pair or trio of students a copy of the first six pictures of Copymaster 5.
I want you to put the pictures in the order that they happened. Put them in a line. Be ready to explain why you put the pictures in that order. - You might allow groups to send out a ‘spy’ to check the order that other groups are using. After a suitable time let the groups ‘tour’ the lines that other groups have created and change their own line if they want to. Bring the class together to discuss the order of events.
Why does this happen before this?
Why does this happen after this? - Do your students recognise the consequential effect of order? e.g. The fire cannot be lit until the hole is dug and there is somewhere to put it.
- Can the students recognise what events occurred between two events? e.g. Covering the food with soil and waiting four hours occurred between putting the food and stones in the hole and taking the cooked food out.
- Discuss:
What might have happened before the hole was dug?
What might have happened after the food was served? - Ask students to draw and caption an event that occurred before the sequence of pictures, and another event that happened after. You could also provide a graphic organiser for students to use. For example, the food must be prepared before or while the hole is dug. It must be bought or gathered before it can be prepared. After the food is served it will be eaten. Copymaster 5, pictures 7 and 8 are before and after pictures.
- Add students’ before and after pictures to the collection from Copymaster 5. You might create a wall display. Some before and after pictures might need to be sequenced. Picture 9 is an event (uncovering the hole) that occurs between two of the six events. Where does it go? Why?
Chances of a good year
In former times, tohunga, wise people of the village, looked at the sky before dawn to watch the rising of Matariki. They used the clarity of the stars to predict what the new year would bring. A clear sky with the stars of Matariki shining brightly signalled a good season for weather and the growing and harvesting of crops. A cloudy sky signalled bad luck.
- At the rising of Matariki, some stars shine brightly while others do not. Each star has a special job. Use PowerPoint 3 to introduce the stars and their jobs. Play a game with Copymaster 6. The first page is a game board. Use the second page to make a set of 12 cards (bright stars, fuzzy stars, and clouds). The second page can be used to make three sets of the cards.
- Put the gameboard down and spread the cards face down on the floor. Mix the cards up while students close their eyes. Students select cards one at a time to cover each of the seven stars. For example, Matariki might be covered by the card for a fuzzy star. Slide 2 of PowerPoint 3 shows a completed gameboard (click through it to place the cards).
If you saw this, what would you predict? - Students should make comments like:
There will be plenty of rain but not too much, and the crops will grow well.
It is going to be a bit windy.
There will be lots of food in the rivers, lakes and sea. - Let students play their own game of predicting the upcoming year. Look to see whether students consider what is on the set of cards in predicting what card might come next.
- After playing the game discuss:
- Is it possible to have a year where every star shines brightly? (No. There are six bright star cards and seven stars of Matariki)
- What is the worst year you can have? (All two clouds and four fuzzy stars come up)
- How likely is it that you will have a good year? (Quite likely since half the cards are bright stars and one third of the cards are fuzzy stars)
Lesson Five
This lesson involves making rēwena paraoa (potato bread). The process of making it takes three stages; preparing the ‘bug’, mixing and baking, then serving. Therefore, it is not a continuous lesson. Preparation and serving food are important activities for Matariki celebrations. It would be beneficial to invite older students, or community members, in to help with this session.
- Explain: In the next three days we are going to make rēwena bread from potatoes. Why is the bread you buy at the supermarket so light and fluffy?
- Some students may have made bread with their parents or grandparents and can talk about yeast as the ‘leavening’ agent. Play an online video of breadmaking and discuss what each ingredient contributes.
- In rēwena bread the natural yeast from potatoes is used to raise the dough. The best potatoes are older taewa (Māori potatoes) which are small and knobbly, but any medium sized aged potato will do. One medium sized potato is needed per recipe (for three students).
- Weighing the potatoes on kitchen scales is a good opportunity to introduce the students to the gram as a unit of mass. Can your students predict the weight of each potato? You might have a potato peeling competition, using proper peelers (not knives). Focus on peeling slowly, with control, as opposed to quickly and without control. The student who gets the longest peel wins. Naturally, you will need to measure the lengths of the peels and come up with a class winner.
- To make one batch of ‘the bug’ cut up the potatoes into smaller bits and boil them in clean water (no salt) until they are soft. You might time how long that takes. Let the potatoes cool and don’t drain the water. Mash the potatoes, water included. Add in (for each recipe):
2 cups of flour
1 teaspoon of sugar
Up to one cup of luke-warm water (as needed to maintain a paste-like consistency) - After you have made a bulk lot of ‘the bug’ put it into clean glass jars to ferment. Fill each jar to one third as the mixture will expand. Cover the jar with greaseproof paper and fix it with a rubber band. Over three of four days the mixture will ferment. Feed it daily with a mix of one teaspoon of sugar dissolved in half a cup of potato water. Your students will be intrigued by the foaming concoction that develops.
- After ‘the bug’ has developed, let your students create their own batch of rēwena bread by following the recipe (PowerPoint 4). This is a good exercise in interpreting procedural language. Read the instructions to the class if necessary or use your most competent readers.
- Once the bread is made it needs to be cut into slices.
How many slices should we make?
How thick will the slices be?
How many cuts will we make? - You might explore sharing slices equally among different numbers of students. Naming the equal parts will introduce fractions. You might explore the different ways to cut a slice in half or quarters.
Dear family and whānau,
This week we have been exploring shapes and sequencing events. Ask your child to find examples of shapes such as triangle, square, hexagon and trapezium around the house. Ask them about how the shapes were used to make stars in class. To extend the work we have been doing on sequencing events, when you are engaging in activities at home that have a defined sequence, ask your child questions to explore before and after actions, for example why does this happen before this? What might happen after we have done this?