Array for quadratics
This unit uses linear and area spatial models to represent and solve linear and simple quadratic equations.
- Represent algebraic expressions as array diagrams.
- Solve for specific unknowns, either areas or side lengths, from array diagrams.
- Expand quadratic expressions with the support of array diagrams.
- Factorise quadratic expressions with the support of array diagrams.
The concept of a variable can be difficult for students to grasp. A variable is a quantity that can take up different values, however, in algebra variables are represented as letters. We often refer to a letter symbol as a variable, when we mean an unknown specific value, a generalised unknown (lots of possible values), or a variable that changes in relation to other variables in a situation.
Before beginning this unit, students have probably solved linear equations. They should recognise the equals sign as an indicator of balance or sameness of quantity, and should understand that equality is conserved if the same operation is applied to both sides of the equation. They might also recognise the importance of inverse operations, i.e. subtraction undoes addition, and division undoes multiplication. Students should also be accustomed to arrays being used as a representation of whole number multiplication.
Research indicates that students often ‘invent’ inappropriate rules for operations on numbers and letters, e.g. 5x + 4x = 20x and 3x – (x + 4) = 2x + 4. Algebraic conventions are not as flexible as those in arithmetic. Therefore physical and diagrammatic representations should be used to support students in checking that their operations make sense.
This unit should follow delivery of linear algebra and linear graphing at Level 5. Students learn to expand and factor quadratic expressions. Quadratic functions have many practical applications, particularly in physics such as speed of a falling body, braking distance of vehicles, and Einstein’s famous formula connecting mass and energy. In this unit the teaching of skills occurs within support of an area model that provides opportunities for discussion and dual development of procedures and concepts. Students who are quick to grasp these concepts will benefit from extension tasks such as those found in the Rich Learning Activities.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- validating students' strategy use, with the aim of moving them towards the use of more efficient strategies
- providing opportunities for students to work in a range of flexible groupings to encourage peer learning, scaffolding, and extension
- constructing a class chart of key ideas, models, and expressions to be used by students as a point of reference
- modelling and providing explicit teaching around the construction of tables, diagrams and graphs, and around the mathematical thinking involved in each stage of the unit. Gradually releasing your level of responsibility allows you to scaffold students towards working independently
- allowing the use of calculators for making predictions and confirming calculations, and to ease the mental load associated with calculation.
The contexts for this unit involve collections of discrete objects (e.g. people, scoops of mochaccino mix). These contexts might be supplemented by, or adapted to, better reflect students' interests, cultural backgrounds, or to make connections to learning from other curriculum areas. Examples might include ratios in cooking, ratios of positions in sports teams or genders in a class, or in the dimensions of human faces. Consider how you can utilise these ratio and rate problems as a way to make connections between mathematics and your students' 'real-world' contexts.
Te reo Māori kupu such as ōwehenga (ratio), hautanga (fraction), whakarea (multiplication, multiply), and pāpātanga (rate) could be introduced in this unit and used throughout other mathematical learning.
Prior Experience
It is expected that students will understand why the area of a rectangle is found by multiplying side lengths, and that the product counts the number of units of area that fill the space. At Level 5 students are also expected to have well-developed calculation strategies with whole numbers. Understanding, and applying, the distributive property of multiplication is particularly important.
Session One
- Begin by presenting some representations of area (perhaps of buildings or areas that are relevant to your students and your local context), and asking students to calculate the area. Animation 1 gives some examples for discussion. Encourage the students to use algebraic notation, e.g. 16w rather than 16 x w.
Key points are:
- The factors multiplied are side lengths but the product counts units of area (squares).
- Unknowns, like m and n, can be used to represent the area, even when the values are not known.
- Slides 7 and 8 provide a problem for investigation.
- How might the problem be written using algebra? (lw = 210)
- What values might l and w take up?
- Can either number be zero? Why not?
- Let the students investigate to find as many solutions as possible. Look for them to be systematic in organising the data. Suggest the use of a table if the data is not organised. You might model this on the board to get students started.
l | w |
1 | 210 |
2 | 105 |
3 | 70 |
5 | 42 |
6 | 35 |
7 | 30 |
… | … |
You may choose to plot the points using a graphing tool to see what pattern emerges.
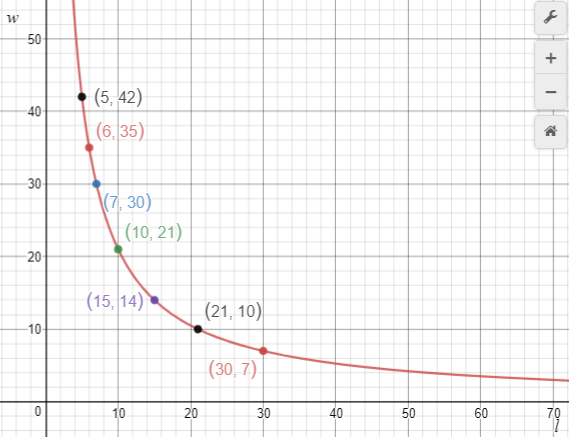
Be open to students creating non-integral values in the ordered pairs, e.g. (1.5, 140), (28, 7.5). It is interesting to zoom in on the point defined by the ordered pair to check that it lies on the graph of lw = 210. Note that in this situation both l and w are variables. This is worth pointing out to students.
- Provide students with Copymaster 1. This asks them to find the value of the specific unknown, using the given side length/s and the given area. Students may use mostly trial and improvement strategies. In doing so they are likely to use estimation to determine plausible values and attend to the structure of each problem. Look for the following:
- Do students divide the area by the known side length to determine the side length that contains the missing value?
- In cases, where the calculated side length has the unknown, plus or minus a constant (e.g. j – 4 = 27), do students make the adjustment? Do they connect the plus or minus to the area diagram (e.g. j is four more than 27)?
- In cases, where the unknown is on both sides, do they apply their knowledge of squares to estimate plausible values? (e.g. z (z – 1) = 182 so plausible values might be 13, 14 or 15)
- Gather together and review the strategies used, solutions, any misconceptions, and the key learnings from the session.
Session Two
In this session students connect expressions with area representations. The expressions involve the distributive property of multiplication at different levels of complexity, and the use of specific unknowns.
- Present Animation 2A and work through the problems given. 7 x 18 is used as a numeric example since students are most likely to apply the distributive property in the form of 7 x 10 + 7 x 8 or 7 x 20 - 7 x 2. The animation encourages students to write different expressions for the same way of seeing 7 x 18. The final slide suggests that arrays can be drawn as boxes rather than needing to show every unit of area. Discuss the answers to the problems posed and address any misconceptions that arise.
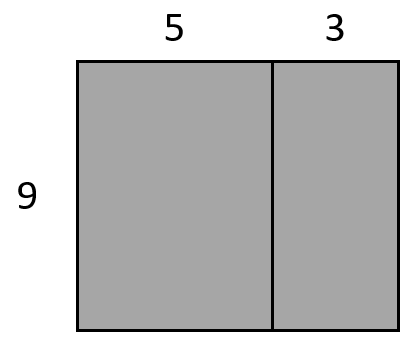
- Ask the students to draw an array to represent 9 x 5 + 9 x 3.
What other expressions could you write for the array? Look for 9 x (5 + 3) and 9 x 8.
- If students need more practice at drawing arrays, provide other examples like (6 + 6) x 4 and 15 x (10 + 3). Show Animation 2B which deals with numeric examples in which both factors are partitioned additively and progresses to the array representing (k + 7)(k + 9).
- Expect the students to recognise that the area can be represented with different equivalent expressions such as:
24 x 16 (20 + 4)(10 + 6) (20 x 10) + (20 x 6) + (4 x 10) + (4 x 6)
35 x 23 (30 + 5)(20 + 3) (30 x 20) + (30 x 3) + (5 x 20) + (5 x 3)
(k + 7) (k + 9) (k x k) + (k x 9) + (7 x k) + (7 x 9) k2 + (9 + 7)k + 63
- Provide the students with Copymaster 2 between two. This task requires students to match each array with two expressions and glue them in the same place in a workbook. The expressions are in factor and expanded form. Look to see if students make structural links such as:
- Look for the side lengths in the factor form.
- Attend to the partial products in the array pictures to find the expanded form.
- Recognise the conventions of recording multiplication, e.g. 7 x h as 7h, 3 x (6 + 4) as 3(6 + 4), and m x n as mn or nm.
Session Three
In this session specific unknowns are introduced using array diagrams. Students are tasked with finding the value of those unknowns.
- Display Animation 3 and wok through the problems as a class. This animation introduces simple problems in which the area of a square is known but the side length is not. Students may be aware that the square root function finds the side length of a square of given area, e.g. √49 = 7 so a square with sides of seven has area 49 square units. The example on Slide 5 represents the equation 11p = 264. Allow students to use estimation strategies if they wish but highlight the efficiency of dividing the area by 11 to find the value of p.
- Use Copymaster 3 (which contains a sequence of problems of increasing difficulty) to encourage students to use structur. Changes to the area make guess and check methods cumbersome. However, changes to the complexity of the side lengths increases the number of solution steps.
The problems are as follows. Students are expected to use their own strategies so the algebraic solutions are for your information.
8r = 840 → r = 105
15(m+4) = 300 → m + 4 = 20 → m = 16
w(w+4) = 437 → w2 + 4w- 437 = 0 → (w + 23)(w - 19) = 0 → w = 19
h(h – 6) = 832 → h2 – 6h – 832 = 0 → (h + 26)(h – 32) = 0 → h = 32
(k + 6)(k + 5) = 240 → k2 + 11k -210 = 0 → (k + 21)(k – 10) = 0 → k = 10
(v + 7) (v – 3) = 459 → k2 + 4k – 480 = 0 → (k + 24)(k – 20) = 0 → k = 20
Session Four
In this session the students use an array model to expand quadratic equations that are in factor form.
- Display Animation 4A. This shows four examples of the form (x + a)(x + b). Work through the problems as a class, and be aware that students may need more practice to become fluent at expanding quadratics in factor form. Animation 4B shows examples of the form (x + a)(x - b) or (x - a)(x + b).
Important points to address are:
- Visualise the area that is represented by the factors
- Consider how the terms in the factors will affect the area, e.g. negatives operating on positives create negative spaces
- Tidying up the partial products by combining x terms.
- Use Copymaster 4 to provide students with more practice at expanding quadratic expressions in factor form.
Session Five
This session is devoted to factorising quadratic expressions.
- Work through Animation 5A together. This deals with the simplest form (x + a)(x + b) of factorising quadratic expressions. Ask students to complete the first four examples of Copymaster 5 for practice. Expect students to connect their diagram with the algebraic factorisation, identifying the important areas, and indicate whether the areas are positive or negative.
- Use Animation 5B to introduce the form (x + a)(x - b) and (x - a)(x + b). Work through the animation as a class. Students should practise examples 5-8 from Copymaster 5 either co-operatively or independently. Animation 5C deals with the form (x - a)(x - b). Work through the animation as a class. Examples 9-12 of Copymaster 5 give practice of factorising this form.
Solutions are as follows:
x2 + 8x + 15 = (x + 5)(x + 3) x2 + 6x + 5 = (x + 3)(x + 2)
x2 + 10x + 21 = (x + 3)(x + 7) x2 + 9x + 20 = (x + 5)(x + 4)
x2 + 5x - 14 = (x + 7)(x - 2) x2 - 5x - 24 = (x - 8)(x + 3)
x2 - 25 = (x - 5)(x + 5) x2 + 6x - 16 = (x + 8)(x - 2)
x2 - 10x + 25 = (x - 5)(x - 5) x2 - 13x + 22 = (x - 11)(x - 2)
x2 - 12x + 36 = (x - 6)(x - 6) x2 - 20x + 64 = (x - 16)(x - 4)
Hello Parents and Caregivers
This week our class is learning about algebra. We will be using an area model to help us to expand and factorise quadratic expressions. Those skills are very important if we want to succeed in future mathematics, particularly calculus.
Please take the opportunity to discuss with your student what they are learning. They may be willing to demonstrate how they solve some of the problems from class.