Tukutuku Patterns
This is a level 3 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (306 KB)
find and apply rules for sequential patterns
square dot paper (see Copymaster)
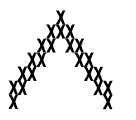
To answer question 1, encourage students to draw the steps of the patterns for themselves on square paper and count the number of crosses that they draw for each step of the pattern. Some students may need help to see the pattern. Others may be able to visualise how the pattern develops without needing to redraw it. They may see that two lots of two are added at each step or that four crosses are added at each step. There are a variety of ways in which students may visualise this. It would be useful to go around the group or class and discuss the different techniques that students are using to visualise the pattern development.
Students could record the number of crosses needed for each step in a table:
This will help them to work out quickly how many crosses are needed. They may also be able to redict the general rule, using the same procedure as that used to find the general rules for the atterns on pages 1 and 2 of the students’ booklet. For this activity, the general rule is: the number of crosses needed for n steps = n x 4 + 2.
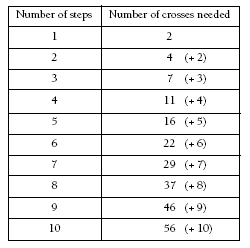
Encourage students to make a table or work out the general rule to answer question 2 rather than drawing all 10 steps. In 2a and 2c, less able students will probably find the tenth pattern by adding on a constant (+ 3 for 2a and + 4 for 2c) while more capable students should be able to find general rules. Question 2b has a pattern that does not involve a constant, so using a table may be the best strategy for all students working on this pattern. Part of the challenge for students may be realising
that a simple rule is not applicable in this pattern.
2a.
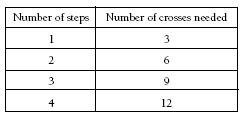
Three extra crosses are added for each extra step. The number of crosses needed for n steps is n x 3.
2. b.
After the initial two steps, each step has one more cross added onto it than was added to the previous step.
2. c.
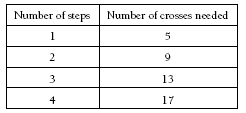
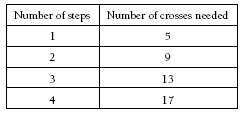
Four extra crosses are added at each step, so the number of crosses needed for n steps is n x 4 + 1.
Answers to Activity
1. a. Answers will vary. The quickest way is to see the first step as 6 crosses and to add 4 crosses for each new step. These 4 crosses could be inserted above the bottom line (the 2 single crosses) each time.
b.
c. 42
2. a. 30
b. 56
c. 41