Open and Shut
This is a level 3 link geometry activity from the Figure It Out series.
Click on the image to enlarge it. Click again to close. Download PDF (618 KB)
explore nets of simple three dimensional boxes
FIO, Geometry and Measurement Link, Open and Shut, page 8
scissors
In this activity, students visualise whether nets can be cut and folded to make open boxes and then check their predictions with the help of the copymaster.
To introduce the activity, ask the students how many faces an open box will have (5). Give each of them a copy of the student book or a photocopy of the copymaster. (If possible, enlarge the copymaster to A3 size for ease of cutting and folding.) Ask them to independently predict which of the nets will make open boxes and then to explain to a classmate why the others won’t.
Introduce and promote the use of these words:
Ask questions such as:
- How many faces are there on Kayleigh’s boxes? (5, not including the invisible “open” face where the lid of the box belongs)
- How many vertices are there on her boxes? (8)
- How many edges are there on her boxes? (12)
- At how many vertices on Kayleigh’s open boxes will 3 faces meet? (4 – the bottom 4 corners of each box) 2 faces? (4 – the top 4 corners of each box)
Following this discussion, have the students check their predictions by cutting out the nets and folding them. When they have done this, ask them what clues they can find in the nets for b, f, and h that show that they won’t make open boxes. Ideas might include:
- “b is a strip. The only two edges that can be joined are the 2 end edges, and if we join them, we will get a 5-sided loop, not a box.”
- “f has the right number of faces and folds but when folded, 2 faces will overlap, meaning that the ‘box’ would have 2 bottoms and be missing 1 side.”
- “h can’t be an open box because it has 5 folds instead of 4.”
Note that while it is possible to draw up some rules and tests that can help us decide whether a net will make a box, the focus should be on teaching students the spatial reasoning skills that will prove useful in a much wider range of situations.
Extension
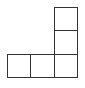
Two-dimensional shapes made from 5 squares joined together are often known as
pentominoes, and they form the basis of many puzzles. There are only 12 different
pentominoes, and 11 of them are illustrated in the activity. Challenge your students to
find the remaining one (pictured at right). Note that a pentomino and its mirror image
are considered to be one and the same piece.
Challenge your students to fit all 12 pentomino pieces together to make (i) a rectangle and (ii) the net of a cube.
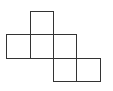
Hexominoes are similar to pentominoes but are made by joining 6 squares instead
of 5. Draw this hexomino on the whiteboard and ask “Could this hexomino be folded
to make a box with a lid? Describe to your partner why you think this.”
Challenge your students to see how many hexominoes they can find. (There are 35.)
They will find that it helps to draw them systematically and to cut them out and rotate
and flip them to make sure that they haven’t doubled up on any. Get them to mark
the hexominoes that could be folded to make a box with a lid.
If students enter pentomino or polyomino into an Internet search engine, they will find many interesting puzzles to try. They will find that doing puzzles of this kind improves their spatial reasoning skills (at the same time as it tests their perseverance!).
Answers to Activity
1. Predictions will vary.
2. These nets can be made into open boxes:
a, c, d, e, g, i, j, k.