Tricky Truncations
This is a level 5 geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (303 KB)
draw nets for three dimensional shapes
- polydrons or geoshapes
- FIO, Level 4+, Geometry, Book Two, Tricky Truncations, page 8
Of the five Platonic solids, three have equilateral triangles for their faces (the tetrahedron, octahedron, and icosohedron), one has squares (the cube), and one has pentagons (the dodecahedron).
Students sometimes think that an octahedron is the same as 2 tetrahedrons joined base-to-base, but this is not the case. When 2 tetrahedrons are joined, the resulting solid has just 6 sides because 2 of the original 8 faces get "lost" in the joining process. An octahedron can, however, be thought of as two square-based pyramids joined base-to-base.
Activity
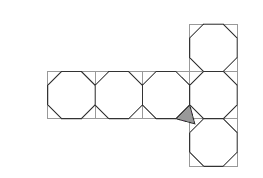
A cube (question 1a) has 6 faces and 8 vertices. Each of the square faces loses a corner in the truncation process, turning the 6 squares into 6 octagons. The 8 corners become 8 equilateral triangles. The truncated part of each corner is a triangular pyramid: 3 isosceles right-angled triangles sitting on an equilateral triangle.
These pyramids are identical to the stellations of the icosahedron in Fantastic Folding (page 9, Geometry: Book One, Figure It Out, Years 7-8).
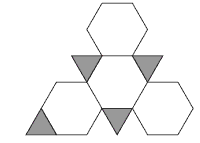
When doing question 1b, the students should begin by drawing the net of a cube and then replace each square with a regular octagon. They should then make an equilateral triangle that exactly matches the side of the octagon and put one of these at each truncated corner. (Only one of these has been placed in the
following diagram.) The triangle can be joined to any of the three adjacent octagons.
If your students are able to use a computer drawing program for this task (and the following ones), they will be able to draw excellent nets using the polygon tool and
the copying, rotating, grouping, and pasting functions. An alternative method is for them to cut patterns from cardboard and draw around these. Both methods remove much of the tedious repetition.
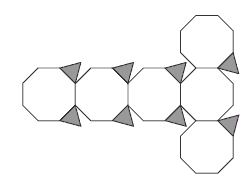
In question 2, the students make a truncated tetrahedron from geoshapes or polydrons, if available, before drawing its net. When drawing the net, the students should start with the net of the untruncated tetrahedron and modify
it. The diagram shows how this can be done. Only one (any one) of the three equilateral triangles at each point belongs to the net, but the other triangles could be used as gluing tabs.
.gif)
When thinking about the shapes they will get from the truncation in question 3, the students should consider:
- The shape of the face of the untruncated solid and what this shape will become when each corner is removed. (The truncated face will always have double the number of sides.)
- The number of faces that meet at each vertex in the untruncated solid. (The vertex will be replaced by a regular polygon that has one side for each of the faces that meet at this point.)
When working out how many there are of each kind of face, the maths is similar for each of the three parts of question 3. As an example, here is the reasoning behind the answers to question 3b:
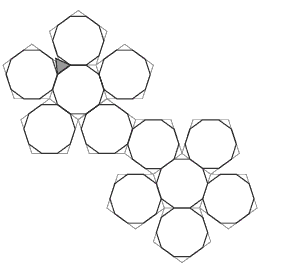
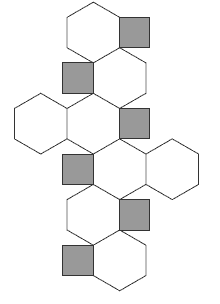
- A dodecahedron has 12 faces, each with 5 sides. When truncated, each of those faces will have 10 (twice as many) sides (that is, each face will be a decagon), but there will still be 12 faces.
- A dodecahedron has 20 vertices. (Each of the 12 faces has 5 vertices, which suggests that there should be 12 x 5 = 60 vertices in the solid. But because 3 faces share each vertex, each is being counted 3 times, so the actual number is 60 ÷ 3 = 20.)
- 3 faces meet at each vertex, so when the dodecahedron is truncated, each vertex will be replaced by an equilateral triangle. There are 20 vertices, so there will be 20 triangles.
This diagram shows the start of a possible net for a truncated dodecagon.
Only one of the small equilateral triangles has been shown. The outlines of the original
pentagon-shaped faces have been left in place. The students are likely to find it easiest if they do this, too.
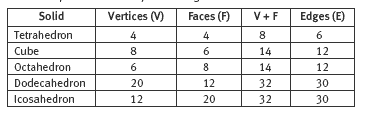
As an extension to this activity, the students could consider the relationship of vertices and faces to edges in the five Platonic solids:
From this, they may be able to generalise that V + F = E + 2, that is, the number of vertices plus the number of faces is always equal to the number of edges plus 2.
There are many websites devoted to the Platonic solids.
Answers to Activity
1. a. 6 octagons and 8 triangles
b. Here is one possible net:
2. a. Practical activity
b. Here is one possible net:
3. a. 8 hexagons and 6 squares
b. 12 decagons and 20 triangles
c. 20 hexagons and 12 pentagons
4. Here is one possible net: