Richard's dice
This problem solving activity has a logic and reasoning focus.

He’d like to rearrange the dice so that only 6's are showing.
There are rules as to how he can move the dice.
He can only pick up a row of three dice or a column of three dice and rotate them together in the same way.
Is it possible for Richard to accomplish this task?
Can you tell him how?
- Find strategies for investigating games.
- Write a solution for a game.
This problem is similar to solving a Rubik’s cube. To solve it students use logic and reasoning. These are very important in mathematics and in the curriculum.
If students choose to use equipment, they should keep track of what they do. As in any problem solving situation, a written record should be encouraged in order for students to be able to justify their solution, or to identify an error made in the process.
Other related Level 5 logic and reasoning problems include Lake Crossing I and Space Crossing.
Note: In recent years mathematicians have analysed a wide variety of games. Analysing games goes back to at least the 17th Century. The famous French mathematician Blaise Pascal (of Pascal’s Triangle) spent a great deal of time studying card games. As a result he laid the foundation for probability and statistics and for a branch of mathematics called Games Theory.
- Nine dice per group
- Copymaster of the problem (English)
The Problem
Richard finds 9 dice arranged in a 3 by 3 square.
He’d like to rearrange the dice so that only 6's are showing.
There are rules as to how he can move the dice.
He can only pick up a row of three dice or a column of three dice and rotate them together in the same way.
Is it possible for Richard to accomplish this task?
Can you tell him how?
Teaching Sequence
- Pose the problem and ask:
How would you get a 6 to the top?
Can you get a whole row of 6s?
How will you record each move? (Diagram, notes) - After some discussion, have the class work on the problem individually or in groups, keeping track of each move.
- Support groups as needed and encourage students to try the Extension when they are ready.
- Have students share and compare their solutions.
Solution
The algorithm has two steps and is based on the fact that when a cube is rotated, a face that is perpendicular to the axis of rotation does not change location. We use ‘left’ to mean the left of the dice; ‘away’ to mean the top in the diagram; and the columns go down the page, while the rows go across.
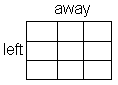
Step 1: Work along a row. For each die pick up the column that it is in and rotate until either the 6 appears in which case leave it showing, or after three rotations of 90 degrees it has not appeared. In this case pick up the row and rotate the row until the 6 appears on top. In both cases the 6 is now on top, pick up the row and rotate it so that the 6 is facing left. This last move ensures that we can move the 6s in a row to the top by a rotation of the columns.
Step 2: After each dice in the row has the 6 facing left, pick up each column in turn and rotate so the 6's are facing up. Pick up the row and rotate so that the 6's are facing away.
Algorithm: Start with the top row using Step 1. Once a die has its 6 facing left, that column is not used again for the other dice in the row.
Do Step 2. Because the 6's are facing away, they are not moved when the column is rotated. It is not necessary to use the first row again. Repeat the algorithm for row 2. Repeat Step One for row 3 but the 6's need only be rotated to the top in Step 2. Rotate Rows 1 and 2 to bring all the 6's to the top.