Discrete data
In this unit as students investigate small amounts of discrete data, they look at how changes in data affect calculated statistics. Building on what they learn, students solve a problem in context from a set of given data.
- Discuss features of small amounts of discrete data.
- Compare features of sets of small amounts of discrete data.
- Plan and conduct an investigation to ascertain information from a set of data.
- Report the results of the investigation concisely and coherently.
In this unit students investigate a collection of scenarios involving discrete data. Various data measures are discussed with regard to their suitability for representing each set of data.
- Answers to questions
- Spreadsheet
- A graphics calculator or spreadsheet would be useful here to help analyse the data
Session 1
This session looks at how small amounts of statistical data can be analysed. Through three examples the importance of mean and range is discussed along with some of the pitfalls associated with statistical analysis.
1. Cricket Scores
A batsman is to be chosen to represent his country. Selectors shortlist two players and study their last six scores:
Batsman A: 98, 94, 2, 0, 106, 0
Batsman B: 48, 49, 54, 50, 62, 37
Discuss with students the suitability of the two batsmen in terms of mean scores and consistency. They choose one to represent his country and give reason(s) for their choice.
2. Netball Scores
A Goal Shoot is to be chosen to represent her country. Selectors shortlist three and study their last available scores:
Goal Shoot A: 11, 13, 12, 14, 10, 12
Goal Shoot B: 8, 18, 15, 9, 12, 16
Goal Shoot C: -, -, 11, 17, 14, 14
Discuss with students the suitability of the three shooters in terms of the mean number of points for each player, their consistency, and the fact that less information is available for one of them. Students choose one to represent her country and give reason(s) for their choice.
3. Rugby Scores
A fullback is to be chosen to represent his country. Selectors shortlist three and have their statistics.
|
|
Conversions |
Penalties |
Tackles |
|
Player A |
8 from 10 attempts |
6 from 8 |
17 from 20 |
|
Player B |
9 from 12 |
6 from 8 |
18 from 20 |
|
Player C |
7 from 10 |
9 from 10 |
8 from 10 |
Discuss with students the suitability of the three players and choose one to represent his country giving reason(s) for their choice.
Sessions 2 and 3
This session looks at how changes in small amounts of data affect mean, median, mode, range and inter-quartile range.
-
Students are presented with the eight data sets relating to test scores for 11 students and asked to describe them qualitatively.
-
In each case students then calculate the mean, mode (if appropriate), median, range, quartiles and interquartile range and draw box and whisker plots.
-
Students comment on their results in light of the qualitative statements made earlier.
-
The test scores all lie between 0 and 10. The data sets can be presented in numerical form, e.g. for set G, {2, 4, 5, 6, 7, 7, 8, 8, 8, 9, 9} or directly in pictorial form as shown here.

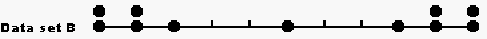
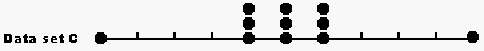





4. Class project
By choosing their own small data sets students investigate the effect of (a) adding a constant value to each item, (b) subtracting a constant value from each item, (c) doubling each item, (d) multiplying each item by a constant amount and (e) adding an outlier to a data set. Students draw general conclusions about what they discover and discuss when such information might be useful.
Session 4
This session is a classroom experiment based on estimating dots on cards.
-
Students are shown seven cards labelled A to G with randomly placed dots on them. (These cards will need to be prepared before hand.)

Card G should have a moderately large number of dots on it (in the data given, a card with 67 dots has been used). The cards are shown to students one at a time in alphabetical order but only long enough for them to guess the number of dots on each card, not count them - the experiment is an exercise in estimation.
-
Students write down their estimates on the sheet provided. The cards A to E are then exposed and the results added to the table. These cards are included to 'set the scene' and establish the routine.
|
Card |
A |
B |
C |
D |
E |
F |
G |
|
Estimate |
|
|
|
|
|
|
|
|
Actual no. dots |
|
|
|
|
|
|
|
|
Error |
|
|
|
|
|
|
|
|
% error |
|
|
|
|
|
|
|
Apart from columns F and G, the remainder of the table is then completed. The inclusion of percentage errors is to show how they increase with the actual number of dots. Someone who is good at estimating will have a percentage error that remains approximately constant.
-
Without exposing card F, the teacher writes up the students’ estimates and they are then discussed and analysed (see riot scenario in the notes below). Only after a decision has been made on the number of dots on card F, based on a statistical analysis of students' estimates, is the card exposed and the dots counted. With a class size of 25 to 30, i.e. with that number of estimates to work with, the analysis more often than not gives the correct answer.
Session 5
This session follows on from the last session with an analysis of the estimates for card G. Alternative data can be used. Teachers may use their class’s estimates or those given in the notes below.
- Discuss the most appropriate way of displaying the data. The range is large and grouping is necessary. How should the data be grouped? How many groups are appropriate?
- Students explore different groupings, decide on one and justify their choice. They then display the data with a bar chart consistent with this choice.
- By determining appropriate statistics (mean, median, interquartile range) and using the bar charts, conclusions are drawn as to the true number of dots on card G.
- Students consider other data sets with different amounts of data and different ranges to decide on appropriate groupings.
- Brainstorm and discuss situations where people make estimates. These might include astronomers when trying to determine the number of stars in a section of sky, DOC scientists estimating populations of birds or sea mammals, reporters estimating crowd numbers, and so on.