Paper Planes: Level 4
In this unit, students investigate changing one variable to see if they can make a paper plane fly the longest. They will need to define what is meant by the longest. They use scatter plots to establish a possible relationship between variables, then use what they have found to make a paper plane to enter a class competition.
- Design an investigation.
- Measure length and time accurately.
- Record data in tables.
- Use scatter plots to display paired numerical data.
In this unit students plan and carry out their own statistical investigation to find out what makes a paper plane fly the longest. Like all such investigations it is important to have a good idea of what data should be collected, how much data is needed and what the limitations of the collecting mechanism are. It is also important that students are clear about which variable they will be changing so that all other variables can be kept constant. Key vocabulary will need introduction and discussion.
This unit also provides an opportunity to focus on decimal notation, to practise measuring accurately, and to prectise converting between units of measure.
Variable
A variable records characteristics of individuals or things. There are two types of variables - categorical and numerical.
Categorical variables
Categorical variables classify individuals or objects into categories. For example, the method of travel to school; colour of eyes.
Numerical variables
Numerical variables include variables that are measured, for example the time taken to travel to school (continuous numerical variables), and variables that are counted, for example the number of traffic lights between home and school (discrete numerical variables).
Scatter plots
A scatter plot (or scatter graph) is a display for paired numerical variables. For example, a sample of students from CensusAtSchool was taken and their heights and arm spans graphed.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- providing a paper plane template to use and direct as to the variable to adjust
- directing the adjustment of variables
- varying the type of analysis and the support given to do the analysis
- providing prompts for writing descriptive statements
- providing teacher support at all stages of the investigation
- promoting the use of calculators to ease the cognitive load associated with calculation
- modelling, and providing direct instruction, around each of the mathematical processes involved (e.g. measuring accurately, creating and recording data in a table, creating a scatterplot)
- utilising technology as a method for creating data displays (e.g. CODAP, Google Sheets, Microsoft Excel)
- organising groups of students to contain students with varying levels of mathematical confidence and knowledge, in order to encourage collaboration (mahi tahi), peer learning (tuakana-teina), and the sharing and justification of ideas
- varying the type of data collected; categorical data can be easier to manage than numerical data. For example, this unit focuses on collecting measurement data about paper planes. One way to adapt it would be for students to research paper planes online and identify the different ways they are classified, collect this information, and display it. For example, paper planes can be classified by airtime/time aloft, speed, distance, stunts/aerobatic, easy through expert to make, category of plane e.g. dart, fighter jet etc.
The context for this unit can be adapted to suit the interests and experiences of your students. The statistical enquiry process can be applied to many topics and selecting ones that are of interest to your students should always be a priority. This investigation focuses on paper planes, however, if your students are more interested in helicopters or waka, the unit could be adapted to focus on making a paper helicopter fly the “longest” or a paper waka sail the “longest”. Consider your students’ current learning and out-of-school interests, relevant and current world-events, and current learning from other curriculum areas. For example, this unit might link to a wider social-sciences context investigating the migration of early Māori and Pacific peoples to New Zealand and historical modes of transport.
Te reo Māori vocabulary such as kauwhata marara (scatter graph, scatterplot) and taurangi (variable) could be introduced in this unit and used throughout other mathematical learning
- Instructions for a variety of different paper planes, search online or have a range of books available
- Access to the internet for statistical software e.g., CODAP Google Sheets, Microsoft Excel
- Stopwatches
- A variety of measuring instruments, including 30 cm rulers, metre rulers, and measuring tapes
- A4 paper
- Paper and pens for recording
Prior experiences
Before working on this unit, students should have engaged in practical measurement exercises where they measured items of varying length using metres, centimetres and millimetres, and measured time using minutes and seconds. They should understand how to measure accurately, and may have some experiences of converting between metric units. Through these experiences, they should have developed some understanding of the relationship between metres, centimetres and millimetres and between minutes and seconds.
Getting started
- Introduce the topic of paper planes to the students by framing the concept in a relevant context (e.g. as part of an instructional writing unit, as part of an investigation into transportation methods). Tell the students there will be a competition at the end of the week to see which plane can fly the longest. They will all be designing their own planes to enter. Encourage them to think about the features of a paper plane that would help it to fly the longest. Record students' ideas on a chart.
What might be meant by the longest? Is this the longest distance, or the longest time, or some other longest?
What features would a plane that can fly a long way have?
What features would a plane that can fly for a long time have?
If you were to make a plane to fly a long way/long time what else would you need to consider? - Allow students time with paper to carry out initial experiments with planes and then brainstorm their ideas about features that affect the distance or time a plane will fly. Discuss these features and introduce the word variable.
- Identify the different numerical variables (i.e. variables that can be measured or counted) that could be involved in the activity.
- how far the plane flies
- how long the plane flies for
- the length of the plane
- the wingspan of the plane
- the number of paper clips on the plane.
- Identify the response or outcome variable that we will be measuring, either length of flight or time of flight, and then discuss how we will measure it (groups might want to do both and the class competition could include both, with their places in each combining to get an overall winner)
- Flight time is the length of time from when the plane leaves the thrower's hand to when it lands on the ground, Which units of seconds, minutes or hours would be most appropriate for time? Why?
- Flight length – throwers must stand behind a line. The place the plane touches the ground is identified (not where it ends up after skidding along the ground). The distance from the line to where the plane touches the ground is measured. Which units of measure, millimetres, centimetres or metres would be most appropriate for distance? Why?
- Identify the possible explanatory variables (the feature of the plane that we will change) and then discuss how they will be measured
- e.g. wingspan – measure from tip to tip
- Identify the different numerical variables (i.e. variables that can be measured or counted) that could be involved in the activity.
- Have students work in pairs to experiment with the different units for measurement, and then facilitate a discussion about the units to be chosen for the class competition.
Which units allow for the greatest accuracy? Why? - If necessary, model accurate measuring using the tools you have provided and the units discussed. This could also be done as a quick, paired activity.
- Set criteria for the materials to be used to make the planes in the following sessions. These criteria need to include a limit on the size of the paper that can be used and details on the numbers and amounts of other materials that can be used e.g. paper clips, tape or staples.
Exploring
Over the next few days have students work in pairs or small groups to carry out investigations using the following steps. Model each of these steps, in the correct order, before giving students the opportunity to start their investigations. Pay attention to the gaps that appear in students’ knowledge and use these to plan small group or individualised teaching sessions. Students may want to research the flight of paper planes before they chose the focus of their investigations.
Investigation Steps
- Make an assertion (a thoughtful statement) on a variable that will affect flight distance/time.
- Choose a basic design for your paper plane, then modify (change the features of) the variable for this design to provide a variety of different models, based on your assertion.
- Decide on how to test each plane, e.g. how many times will you throw the plane at each distance, how will you decide which outcome measure best represents for the variable (feature) chosen
- Collect data by trialling each plane and recording the distance/time it flies alongside the variable (e.g. wingspan, plane length) you are testing. This can be done by recording the data in a spreadsheet or in a table in a statistical software package such as CODAP.
- Plot data on a scatter plot to establish whether there is a relationship between the variables you are investigating. This can easily be done using CODAP or spreadsheet software, see Cars for ideas on plotting scatter plots using CODAP.
- Check your assertion. Was your original idea correct? Modify your plane design accordingly.
Example Investigation
- Assertion: a longer wingspan will help a paper plane fly a greater distance.
- To test the assertion about wingspans several planes with varying wingspans are required.
- Decided to test each plane three times and record the middle measurement.
Data collected as below:
| Plane | Wingspan | Middle flight distance |
| 1 | 5.2 cm | 3.2 m |
| 2 | 7.5 cm | 5.6 m |
| 3 | 10.3 cm | 6.1 m |
| 4 | 14.8 cm | 6.4 m |
| 5 | 18.0 cm | 8.9 m |
Data plotted as below 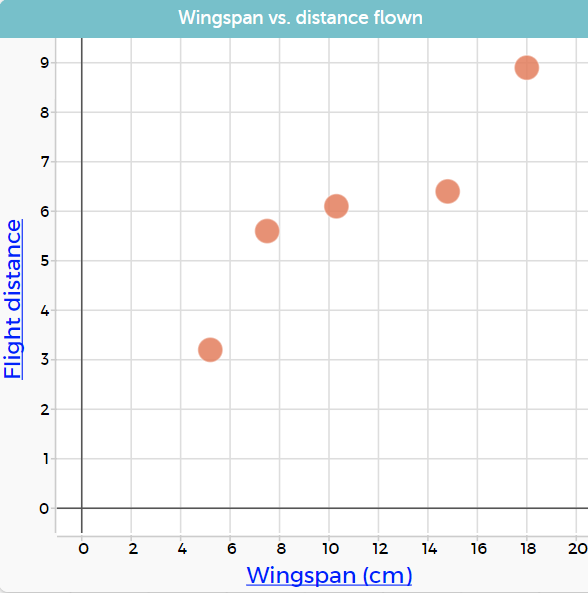
As the wingspan increases so does the distance flown.
As investigations are carried out the following points may need to be discussed with the students.
- For the investigations to be a fair test only one variable can be altered across each of the planes to be tested. The planes need to be the same in every respect other than the feature being tested.
- The number of trials needed for each plane should be considered carefully. In scientific contexts 3-5 trials are often used, pragmatically because of time constraints. This is usually sufficient to see if there are any outliers. At higher levels the mean is also taken, but for this level we will use the middle value when placed in order (median).
- The best way to record and plot the data.
- Is all data plotted or an average e.g. the middle value (median) for each different set of trials?
Reflecting
- Hold a competition to see which plane flies the longest. Ensure accurate measurements are taken of distances flown or times taken.
- After the competition reflect on the most successful planes.
What evidence did we have that those planes would be the most successful?
If we were going to hold another competition which features could we combine to produce a very successful plane?
Was there anything fair or unfair about our investigation? - If time permits, students could be given the opportunity to create a display that demonstrates their mathematical understanding in an appropriate format (e.g. video, oral or digital presentation, poster or infographic, written summary, by acting it out).
Dear parents and whānau,
This week at school we are making paper planes and measuring how far they can fly. Ask your child to share their design with you and offer some suggestions of things they could try to improve the design of their plane. If you have access to the internet or other references available, please help your child spend some time researching flight at home so that everyone can report their findings back to the class.