Seed Packets
Solve division problems involving fractions.
Solve simple rate problems using multiplication.
Number Framework Stages 6 and 7
Using Materials
Problem: Make up some packets of make-believe seeds. Similarly, candy bars could be made with cubes. Begin with a 1:2 ratio, for example, one blue seed and two yellow seeds in each packet. Get the students to make up similar packets.
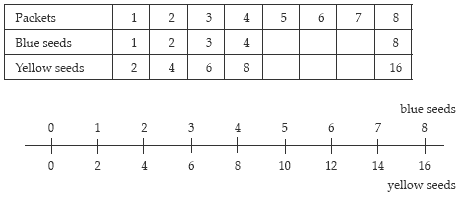
“Suppose we wanted a box with eight packets in it. How many blue seeds and how many yellow seeds would be in the box?”
Allow the students to use materials to solve the problem. Reflect on their strategies.The students will commonly put together copies of one packet until eight packetsare formed.
Record this “build up” in a ratio table or a double number line:
Pose predictive problems like:
“If we had 14 packets, how many yellow seeds would there be?”
Since doubles are involved, the students will fi nd it easy to apply addition methods to this situation.
To encourage multiplication, make up more complex ratios. Some examples are: “Three red and two yellow seeds are in each packet. In the box are nine packets.
How many seeds of each colour are in the box?”
“One blue seed and three red seeds are in each packet. Ten packets are in the box.
How many seeds of each colour are there in the box?”
Using Imaging
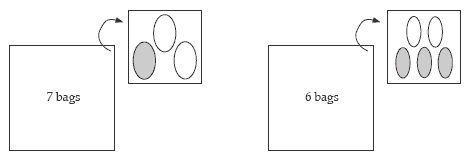
Shielding: Create examples of ratio problems using bags of beans or connected cubes. Put several of these bags or stacks into an empty tin can. The outside of the can may be labelled with how many bags are in the can. The students are shown one or two bags and asked to work out how many beans or cubes of each colour are in the can.
Encourage the students to use double number lines and ratio tables to show their strategies. The students can make up mystery-can problems for others to solve.
Using Number Properties
Increase the number of bags involved while keeping the ratios simple (for example, 1:3, 2:3, 2:1, 6:4). This will make the addition strategies less effi cient and motivate the students towards multiplicative thinking.
For example: “Each bag has two red and four yellow beans. There are 20 bags in the can. How many beans of each colour are in the can?”
Recording
Students can work through written examples, such as, “There are two green beans and three red beans in each bag. How many red beans would go with 14 green beans?”