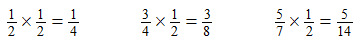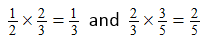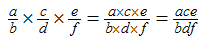This unit explores how the properties, that hold for multiplication and division of whole numbers, also apply to fractions (commutative, associative, distributive, and inverse). The operations of multiplication and division can be developed using a length model (Cuisenaire rods). While the size of the referent one (whole) is fixed at first, students need to be able to change the referent during the physical process.
- Name the fraction for a given Cuisenaire rod with reference to one (whole) and with reference to another rod.
- Fluently multiply two or more fractions.
- Divide a fraction by another fraction, including when the divisor is greater than the dividend.
‘Fractions as operators’ is one of Kieren’s (1994) sub-constructs of rational number, and applies to situations in which a fraction acts on another amount. That amount might be a whole number, e.g. three quarters of 48, a decimal or percentage, e.g. one half of 10% is 5%, or another fraction, e.g. two thirds of three quarters. Students often confuse when fractions should be treated as numbers and when they should be treated as operators, particularly when creating numbers lines, e.g. place one half where 2 1/2 belongs on a number line showing zero to five.
Fractions can operate on other fractions, and the rule for fraction multiplication can be generalised, a/b x c/d = ac/bd. The commutative property holds since c/d x a/b = ac/bd as do the distributive and associative properties, though the former is mostly applied in algebra rather than number calculation. In order that the inverse property holds, i.e. division by a given number undoes multiplication and vice versa, the following must be true:
a/b x c/d x d/c = a/b because c/d x d/c = 1 so division by c/d must be equivalent to multiplication by d/c.
Specific Teaching Points
Understanding that fractions are always named with reference to a one (whole) requires flexibility of thinking. Lamon (2007) described re-unitising and norming as two essential capabilities for students to develop if they are to master rational numbers and other associated forms of proportional reasoning. By re-unitising it is meant that students can flexibly define a given quantity in multiple ways by changing the units they attend to. By norming it is meant that the student can then act with the new unit. In this unit, Cuisenaire rods are used to develop students’ skills in changing units and thinking with those units.
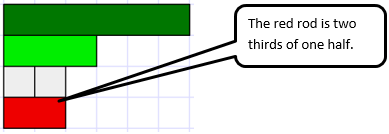
Multiplication of fractions involves adaptation of multiplication with whole numbers. Connecting a x b as ‘a sets of b’ (or vice versa) with a/b x c/d as ‘a b-ths of c/d’ requires students to firstly create a referent whole. That whole might be continuous, like a region or volume, or discrete, like a set. Expressing both fractions in a multiplication and the answer require thinking in different units. Consider two thirds of one half (2/3 x 1/2) as modelled with Cuisenaire rods. Let the dark green rod be one, then the light green rod is one half.
So which rod is two thirds of one half? A white rod is one third of light green so the red rod must be two thirds. Notice how we are describing the red rod with reference to the light green rod.
But what do we call the red rod? To name it we need to return to the original one, the dark green rod. The white rod is one sixth so the red rod is two sixths or one third of the original one. So the answer to the multiplication is 2/3 x 1/2 = 2/6 or 1/3.
While the algorithm of ‘invert and multiply’ is easy to learn and enact, understanding why the rule holds requires complex thinking. Yet the ability to re-unitise and norm are central to fluency and flexibility with rational number, and therefore necessary for algebraic manipulation. Consider a simple case of division of a fraction by a fraction, 2/3 ÷ 1/2 = 4/3.
If the dark green rod is defined as one then the crimson rod represents two thirds and the light green rod represents one half.
If we adopt a measurement view of division rather than a sharing view the problem; 2/3 ÷ 1/2 = ? translates into “How many light green rods fit into the crimson rod?” So the light green rod becomes the new referent. The result is that one and one third light green rods make a crimson rod. Note that; 1 1/3 = 4/3.
As a check that the inverse property holds with our answer, we might calculate 4/3 x 1/2 = 4/6 = 2/3 in the same way that we could check 24 ÷ 3 = 8 by calculating 8 x 3 = 24.
This unit is set for students to learn, and practice, outcomes at Level 5 of mathematics in the New Zealand Curriculum. Differentiation involves simplifying or adding more challenge to the tasks in the following ways:
- varying the level of abstraction, that is the extent to which operations are carried out mentally rather than through actions on materials. Cuisenaire rods are the manipulatives used in the unit. Encourage abstraction by asking predictive questions, e.g. “What fraction do you think will be the difference between x and y?”
- making clear links between the numerator as a counter, and the denominator as the number of parts in a whole. Link fraction symbols with the Cuisenaire rod models students create
- controlling the fractions used in the problems so they can be physically modelled before extending the range of fractions to numbers outside what can be easily modelled. Halving related fractions, i.e. quarters, eighths, sixteenths, etc., tends to be easier than fractions with odd denominators, i.e. thirds, fifths, sevenths, etc.
- managing the reading and recording demands of tasks, particularly by allowing students to record their thinking in their own way before supporting them toward conventional symbolic recording
- encouraging students to work collaboratively in partnerships, and to share and justify their ideas (a tuakana/teina relationship could be used)
- modelling the mathematics involved, and practicing the gradual release of responsibility to scaffold students towards making the calculations independently
- regularly sharing ideas with the whole class.
The context for this unit is not real life. However, a story shell such as construction beams, waka lengths, or steps, might be used if there is potential to motivate students. Most students will enjoy the opportunity to work with Cuisenaire rods.
Te reo Māori vocabulary terms such as hautanga (fraction), hautau ōrite (equivalent fraction), tauira (patterns), tauraro (denominator), whakarea (multiplication) and taurunga (numerator) could be introduced in this unit and used throughout other mathematical learning.
- 1 cm squared paper
- Cuisenaire rods or access to the online Cuisenaire rods tool
- Copymasters One, Two and Three
Prior Experience
Students are unlikely to have previous experience with using Cuisenaire rods since the use of these materials to teach early number has been abandoned. Their lack of familiarity with the rods is a significant advantage as they will need to imagine splitting the referent one to solve problems. However, other units in the Cuisenaire rod fractions collection are available at level 3 and level 4.
Session One
- Use Cuisenaire rods or the online tool to introduce multiplication of fractions in the following way.
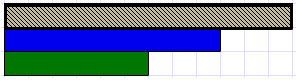
Set up this diagram:
- Tell the students that these rods can be used to represent fractions. Pose the following questions and ask students to discuss their answers to each with a partner.
“If the blue rod is defined as one then what fraction is the dark green rod?” (two thirds)
“What coloured rod is half of two thirds?” (light green)
“Relating back to the blue rod what fraction is one half of two thirds? In other words, what fraction is the light green rod?” (one third)
“How can we write one half of two thirds as an equation?” (1/2 x 2/3 = 1/3)
Note that your students might not relate multiplication of whole numbers, e.g. 3 x 8 = 24, with ‘of’ as a function. If this understanding is not evidenced, spend some time developing it. See the Level 3 unit Multiplying Fractions for more information.
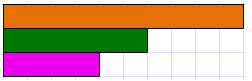
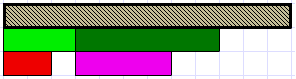
- Create this diagram:
- Pose the following questions and ask students to discuss their answers to each with a partner.
“Let’s try a more difficult example. If the orange rod is one, what fractions are the dark green and crimson rods?” (dark green is six tenths or three fifths, crimson is four tenths or two fifths)
“So what fraction of the dark green rod is the crimson rod?” (four sixths or two thirds)
“How can we record two thirds of three fifths as an equation?” (2/3 x 3/5 = ?)
“What is the answer to the equation?” (2/3 x 3/5 = 2/5)
- Record the two equations that you have results for:
1/2 x 2/3 = 1/3 and 2/3 x 3/5 = 2/5
- Ask: “can you see any patterns here? Two examples are not enough really.”
Students might notice that the same digits are on the / diagonal or that the denominator of the answer matches the denominator of the second fraction. However, there is no clear relationship in the equations since equivalence is involved.
- Explain: “our goal today is to find a pattern that allows us to solve any problem like this, where a fraction is multiplied by a fraction.”
- Ask the students to work in small co-operative groups using Copymaster One. Each group will need access to a set of Cuisenaire rods or to the online Cuisenaire rods tool.
Roam and look for the following:
- Can students identify and name the fractions for each rod when told the referent one rod? To do so they will need to partition the rods into smaller equal units using the other rods that are available.
- Can students accept the third rod as a unit of measure? To do so they need to consider how many of that unit fit into the second rod. This idea is particularly challenging where the third rod is larger than the second rod.
- Can students map back to the original one to name the result of the fraction multiplication?
Identify, and make note of, any gaps in knowledge or misconceptions. Use these as the basis for a teaching session with the relevant students, or for a whole-class review.
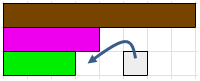
- After a suitable period of investigation bring the class back together to discuss how they solved the problems. Record the first three solutions:
- Ask: “is there a pattern in these three examples?” Look for students to notice that the numerators and denominators of the factors are multiplied to give the numerator and denominator of the answer.
- Display the following two equations and ask “does this pattern apply to our first two examples?”
- Direct the students to multiply numerators and denominators to see if the pattern holds. They may notice that the answers are equivalent to the products, i.e. , 2/6 = 1/3 and 6/15 = 2/5. If your students have difficulty with equivalence it may be worthwhile taking some sessions from Cuisenaire Rod Fractions: Level 4.
- Focus on examples 6a and 6b from Copymaster One. In both cases, the multiplier factor is an improper fraction. This idea is challenging but important if students are to generalise multiplication of fractions. In 6a the diagram models if the brown rod is one, then the crimson rod is one half, and the blue rod is nine eighths since each unit square is one eighth of the brown rod. The difficulty is in recognising that the blue rod is nine quarters of the crimson rod. This relationship requires the students to use the blue rod as the measure of the crimson rod.
- Ask “does the rule for multiplying fractions hold if one of the fractions is improper?” and discuss students' ideas (Yes, e.g. 5/4 x 2/3 = 10/12 = 5/6, for 6b).
- As a class, record a summary of the important points covered in the lesson. This could be kept as a class chart and used by students as a point of reference. Look for students to identify the following points:
- 'of' and 'times' are interchangeable
- we can use a pattern (e.g. numerators and denominators of the factors are multiplied to give the numerator and denominator of the answer) to work out the answer to some multiplication problems with fractions.
Session Two
The purpose of this session is to consolidate understanding of the multiplication of fractions, and to see if the properties of whole numbers under multiplication hold for fractions as well.
- Review the key points from the previous session and address any misconceptions. You might ask students to do this in small groups or pairs.
- Create the diagram shown below for the students and ask “what fraction multiplication is represented in this diagram?” (2/3 x 3/4 = 6/12 = 1/2)
- Give the students 5-10 minutes, in small groups, to come up with their own multiplication of fractions examples. Ensure they record their examples using squared paper and an equation.
- Gather the class together and discuss students' work, with a focus on the properties of multiplication.
- Present the following three equations and ask “which of these equations are true? Explain how you know.”
5 x 3 = 3 x 5 4 x 2 x 3 = 3 x 4 x 2 3 x 7 = 3 x 2 + 3 x 5
All three equations are correct as they are examples of the properties of whole numbers under multiplication. Look for students to explain that the first equation is the commutative property, the order of the factors does not affect the product. The second equation is less obvious as it applies the associative property which is about the pairing of three of more factors not affecting the product. Since multiplication is a binary operation only two factors can be operated on at once. Students may recognise that in the third equation seven is distributed into five plus two.
- Ask a student to draw a diagram of how this example works. For example:
- Record the properties under each equation.
“Do these properties also hold for fractions when they are multiplied? Let’s work on the example we started with.”
“If the commutative property works for fractions what should be true about; 2/3 x 3/4 = 6/12 = 1/2?”
Students should connect to the whole number example and say that 3/4 x 2/3 = 1/2 as well. Begin with the same stripy rod for one (12 unit squares).
“Which rod is two thirds?” (brown)
“Which rod is three quarters of two thirds?” (dark green)
“What fraction of the one rod is the dark green rod?” (one half)
“So from this one example the commutative property seems to work. See if it works with the fraction multiplication you made up.”
- Let the students work out if the commutative property works for their example. Gather the class and choose a couple of further examples to share. Expect that some students will argue that the property obviously holds for this reason. If the commutative property holds for whole numbers under multiplication it must also hold for fractions.
- Return to the original example of, 2/3 x 3/4 = 6/12 = 1/2.
Ask “what fraction multiplication is this diagram representing?” 1/2 x 2/3 x 3/4 = ?
“What is the answer?” 1/2 x 2/3 x 3/4 = 6/24 = 1/4.
“If the associative property holds what also will be true?” Students should offer several possible examples, e.g. 2/3 x 3/4 x 1/2 = 1/4.
- Ask students to check if the other examples of pairing factors first give one quarter as the answer.
“From what we know about the commutative property, why must this be true?” Look for students to argue that a similar generalisation is possible because:
- The distributive property is harder to illustrate with fractions than with whole numbers. Start with the original example; 2/3 x 3/4 = 6/12 = 1/2. “Three quarters is made up of one quarter plus one half. If the distributive property works, what must also be true?” 2/3 x 3/4 = 2/3 x 1/4 + 2/3 x 1/2.
- Challenge the students to work together in small groups to see if this example is true. Look for them to work between the symbols and the Cuisenaire rod model.
Replacing the blue rod with the light green (one quarter) and dark green (one half) gives this:
Finding two thirds of each rod (light green and dark green) gives:
- Ask “do two thirds of one quarter and two thirds of one half combine to make our original answer, one half?” (Yes, since red and crimson rods combined make a dark green rod).
“While one example is weak evidence it appears that the distributive property might work for fractions under multiplication.”
- If time permits asks your students to try out the distributive property for other fractions. Note that the distributive property is most commonly applied when working with mixed numbers, e.g. 3/4 x 1 2/3 = 3/4 x 1 + 3/4 x 2/3.
Session Three
In this session the purpose is to find the quotient of two fractions by division. A measurement view of division is used rather than a sharing view.
- Pose this simple problem: “A group of four students make $72 on a job. If they share the money equally how much should each friend get?”
- Ask your students to solve the problem and share their strategy and solution with a partner. Students should recognise it as a division problem, 72 ÷ 4 = 18. There are many ways to solve the problem but the main focus is interpretation of seventy-two divided by four. Most students will ask themselves, “How many fours are in seventy-two?” which is measuring 72 in sets of four. Expect strategies like:
- “If they got $80, that would mean $20 each. So they got $2 less each, that’s eighteen dollars.”
- “If there were eight students they would get $9 each. There are half as many students so they should get twice as much.”
- Record 72 ÷ 4 = 18 on the board and write 72 ÷ 1/2 = ?, as well.
Discuss: “Ninety-five percent of people get this problem wrong. Try to solve it yourself then talk to your partner to justify your answer.”
- In the discussion that follows try to connect their interpretation of 72 ÷ 4 as “How many fours are in seventy-two” with the meaning of 72 ÷ 1/2 as “How many one halves are in seventy-two?”
“Why is the answer, 144, larger than the dividend, 72?” You may need to use a simple example to convince some students. Make a Cuisenaire rod model like this:
- Discuss:
“If the crimson rod is one how many ones do I have?” (five)
“What fraction are the red rods?” (one half)
“How many halve do you get in five ones?” (ten)
Record this as 5 ÷ 1/2 = 10. “So the important idea is that we treat division as a ‘How many goes into’ operation.”
- Create this simple example of fraction division using Cuisenaire rods. Build up the model as students answer.
“If the crimson rod is one half, then what colour is the one rod?” (brown)
“So what fraction is the light green rod?” (three eighths)
The model should now look like this:
- Pose the question, “How many three eighths fit into one half?” Record 1/2 ÷ 3/8 = ?
- Ask the students to attempt an answer themselves then talk to a partner to justify their answer. Some students will provide answers like “A bit more than one” but encourage them to be accurate.
An important point is that the crimson rod (one half) is being measured with the light green rod (three eighths) so the light green rod is the measurement unit the answer must be expressed in. Many students will notice that a white rod fits into the ‘gap’.
- Discuss: “How much of a light green rod is the white rod?” (one third)
“So we get an answer of one and one third. What is that number as a fraction, not a mixed number?” (four-thirds)
Record; 1/2 ÷ 3/8 = 4/3. Mention that equivalence fooled us last time with the multiplication rule.
- Discuss: “Write down some equivalent fractions for four thirds.” (8/6, 12/9, 16/12...)
“If I write 1/2 ÷ 3/8 = 8/6 do you notice a pattern from one example?”
- Get the students to work on the problems in Copymaster Three which scaffolds their learning towards division of fractions. Ask them to work in small co-operative groups with a set of Cuisenaire rods, or the online tool, and squared paper to record their ideas. Look for the following:
- Are the students able to accept the second rod as the unit of measure and express the answer in terms of that rod?
- Do the students generalise that 1 ÷ a/b = b/a?, for example 1 ÷ 7/10 = 10/7.
- Can they explain why 1 ÷ a/b = b/a?
- Do they recognise that if the fractions have a common denominator then the division operates like whole number division?, e.g. 5/8 ÷ 3/8 has the same answer 5 ÷ 3 as because the units (eighths) are the same.
- Do they generalise that if 1 ÷ a/b = b/a then using any fraction as the dividend just ‘scales’ the answer? For example, if 1 ÷ 4/5 = 5/4 then, 1/2 ÷ 4/5 = 1/2 x 5/4.
- After a suitable period of investigation bring the class back together to discuss the points about. Use selected examples, as above, to ask students to reflect on a general rule for division of fractions. The discussion should lead to two useful algorithms. Use this example:
Express both fractions as equivalent fractions:
5/10 = 1/2 (Yellow rod) and 8/10 = 4/5 (Brown rod) so 1/2 ÷ 4/5 = 5/10 ÷ 8/10.
Since the units are all eighths the problem is just like “How many lots of eight somethings fit into five somethings.” Be aware that students might be unaware of the quotient rule for rational numbers, a ÷ b = a/b, for example 5 ÷ 8 = 5/8.
Invert and multiply:
The most common algorithm, and that needed for algebra, derives from, 1 ÷ a/b = b/a. So the answer is the reciprocal. Any change to the dividend, one, is just a scalar so in general, c/d ÷ a/b = c/d x b/a.
Session Four
The aim of this session is to consolidate students’ connection between multiplication and division of fractions. To do so we keep the representation the same, Cuisenaire rods, but we expect a considerable amount of re-unitising and norming with the units that are created.
- Begin with this simple arrangement of three rods:
- Ask a series of “Can you see…?” questions. Expect students to discuss the questions in ‘think-pair-share’ format. Write the equations as well as saying the question.
“Can you see five eighths of four fifths? (5/8 x 4/5 = ?)” The yellow rod is five eighths of the brown rod which is four fifths of the orange rod.
“Can you see how many one halves fit into four fifths? (4/5 ÷ 1/2 = ?)” The yellow rod is one half, the brown rod is four fifths.
"Can you see how many four fifths fit into one half? (1/2 ÷ 4/5 = ?)”
“Can you see eight fifths of one half? (8/5 x 1/2 = ?)”
All of the above questions treat the orange rod as one.
- Ask: “What ‘Can you see?’ questions could we ask if we treated the brown rod as one?”
For example; “Can you see two times five eighths? (2 x 5/8 = ?)” or “Can you see how many five quarters fit into five eighths? (5/8 ÷ 5/4 = ?)”.
- In small groups of two or three challenge your students to do the following:
- Choose a set of three different Cuisenaire rods.
- Create as many “Can you see…?” problems as they can with that set.
- Produce a published set of their problems with answers hidden somewhere for other students to solve. Problems should involve pictures, words and equations. You could require students to frame these within a specific context, or ask students to come up with a context that is relevant to them, their lives, or learning from other curriculum areas.
Students might publish their problems as a word document or PowerPoint so that the sets can be published. Swapping problems among groups is an excellent way for students to check if their reasoning is correct as well as providing practice at re-unitising.
- After sufficient time ask some groups to share their favourite “Can you see…?” problem. Look for other students to:
- Identify which rod is being used as the referent one rod
- Name the other two rods in terms of that one rod
- Connect word stories to appropriate multiplication or division equations
- Solve the equations and explain their answers with reference to the Cuisenaire rod model
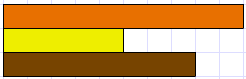
Dear families and whānau,
This week, students will be learning about multiplication and division of fractions, for example “What is two fifths of one half?” We will be using some materials called Cuisenaire rods which are lengths of plastic or wood. Here is a Cuisenaire rod model as an example.
Your son or daughter should be able to identify the orange rod as one and name the fractions for the other rods. The yellow rod is one half and the red rod is one fifth, in this case. Also the red rod is two fifths of the yellow rod.
Feel free to explore and use this online Cuisenaire rods: https://mathsbot.com/manipulatives/rods