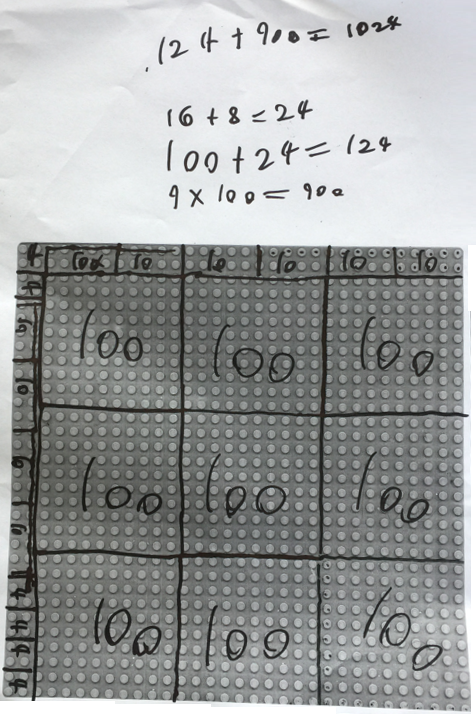
This counting collections activity engages students in finding the number of studs on a Lego (or similar) baseplate.
A collection presented as an array can be estimated, organised and grouped strategically for an efficient and accurate count. Arrays are useful for building multiplicative thinking. They can be used to explore calculations such as 13 x 5 where the array can be split into useful chunks. This means that children can use their known number facts to work out calculations. Students can represent their strategies and counts with numbers, symbols, words and diagrams.
Counting collections promotes number sense, and is an essential foundation for students to be successful mathematicians. Recent literature (e.g. Boaler, 2008) suggests that flexible grouping practices best supports equitable opportunities for student learning.
It is important to share the mathematical focus of the task with students. This task promotes multiplicative thinking through presenting a collection to be counted as an array. An array enables students to form useful mental pictures to support the generalisation of number properties (e.g. commutative and distributive properties). The task provides students with opportunities to partition the array strategically to make the count easier, to work collaboratively, to record their strategies and to share and justify their counts and strategies using a variety of representations. The progression in the sophistication of students’ thinking when asked to count a collection of objects goes from counting in ones, to counting in groups, reasoning additively to reasoning multiplicatively.
Consider the mathematical language your students are likely to use when grouping and counting, and the language you want to develop.
Student agency is promoted if students have choice over their own counting and recording methods. Rather than suggesting particular solution or counting methods to students, teachers can use enabling prompts to support students who require assistance. Extending prompts can be offered when students have completed the task to build more sophisticated strategies and understandings.
- Building brick base plates (for example, Lego or Duplo).
- Building bricks of various sizes
- Photocopies of base plates for students to manipulate
Task Introduction
The wondering for this mathematical inquiry is:
- I wonder how many studs there are on this base plate? (A variety of sizes could be made available to cater for the range of abilities of your students.)
Considerations when planning for the task introduction include:
- Do the students understand the context of the task?
- What key mathematical ideas and language do teachers need to clarify with students in order for them to engage with the task?
Student Exploration of the Task
- While students are exploring the task, listen to their mathematical language and thinking, particularly around grouping multiplicatively.
- If students are struggling to get started enabling prompts can be offered, but only once students have had sufficient time to struggle with the problem themselves.
Examples include:
Start with counting this part of your collection.
How could you partition this collection to make it easier to count them all?
- Extending Prompts can be offered if students finish quickly or find the task easy. They encourage higher order thinking and generalisation within the same task.
Examples include:
Reorganise the grouping of that collection to count it more efficiently.
I wonder how many of these bricks (e.g. 2x4 bricks) would be needed to cover the base plate completely?
Can you arrange them so that you can cover it perfectly?