In Your Prime

Exploring factors and prime factors enables students to use their knowledge of basic multiplication facts as they make observations about numbers. This will help them later when they work with fractions and simplify algebraic expressions. The students may work in small groups or individually. Small-group work will have the advantage of introducing the students to a range of possible solutions.
The students can attempt question 1 randomly with cards, but you could encourage a more systematic response by asking “How do you know you’ve got them all?”

In the initial discussion for question 2, or if the students need help later, you could use a range of examples, such as 3 x 5 x 7, 2 x 5 x 5, and 3 x 3 x 3, to help clarify the types of equations that are possible. Again, as in question 1, sharing ideas in a group can lead to a range of possible solutions being recorded, perhaps in a systematic table. Class discussion should revolve around recording all the possible numbers and making sure that none are missed. Again, you could extend the question by including the fifth prime number, 11.
As a follow-up investigation, you could ask “Can all the numbers from 1 to 50 be products of these cards? What is unusual about the numbers that can’t? How about the numbers from 51 to 100?”
For question 3, you need to discuss two types of whole numbers: prime numbers and composite numbers. A prime number is a number greater than 1 that is divisible only by itself and 1. A composite number is any number that is not prime, that is, it has more than two factors.
Ask your students: “Is 57 prime or composite?” Discuss other examples such as 19, 21, 29, 27, and so on, and the special nature of 1. (1 is not considered a prime number because 1 = 1 x 1 is one times itself, with no other factor involved, and therefore it breaks the pattern. See also the sieve of Eratosthenes, which is
described in the notes for page 4 of the students’ book.) The students can also look up the word “prime” in their dictionaries and record definitions related to the mathematical meaning.
At this stage, they may not have a formal prime factorisation strategy, so they may link question 3 to the earlier questions and try other combinations of 2, 2, 3, and 5. To deter them from rearranging the factors given, a note has been added to the question.

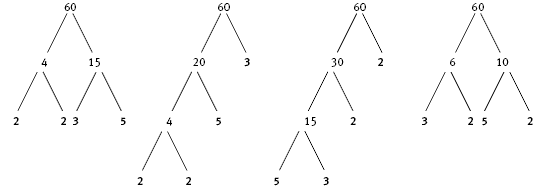
The students can verify the answer by splitting composite numbers into their factors until there are no more composite numbers to split, using a method known as a factor tree. For 60, this is:

Regardless of how the composites used to initially split the 60 are ordered, you end up with the same set of prime factors (2, 2, 3, 5).
You could ask your students to complete factor trees for three other specific numbers after you have modelled 60 with them. They could then investigate their own choice of composite numbers.
Question 4 requires the students to list all the factors of a number (both composite and prime). Mei Ling’s method is quite logical and systematic. Starting at 1, she moves systematically through paired factors of 60 until she reaches the halfway point, which is after 6 x 10. Beyond that, because of the commutative property of multiplication, the factors are just reversals of the previous ones (for example, 10 x 6).
Hine’s method is really using the factor tree system in reverse, but this can get confusing, and the students will need to be systematic in keeping track of how they have used parentheses to make the different groups.
You can organise further practice in finding sets of factors and prime factors by having groups chart and share their solutions to different numbers, for example, 36, 24, 336, and so on.

Answers to Activity

1. a. 10, 14, 15, 35
b. 4, 9, 25, 49
2. 2 x 2 x 2 = 8, 2 x 2 x 3 = 12, 2 x 2 x 5 = 20,
2 x 2 x 7 = 28, 2 x 3 x 3 = 18, 2 x 3 x 5 = 30,
2 x 3 x 7 = 42, 2 x 5 x 5 = 50, 2 x 5 x 7 = 70,
2 x 7 x 7 = 98, 3 x 3 x 3 = 27, 3 x 3 x 5 = 45,
3 x 3 x 7 = 63, 3 x 5 x 5 = 75, 3 x 5 x 7 = 105,
3 x 7 x 7 = 147, 5 x 5 x 5 = 125, 5 x 5 x 7 = 175,
5 x 7 x 7 = 245, 7 x 7 x 7 = 343
3. a. No.
b. The factor order can be rearranged (for example, 5 x 3 x 2 x 2), but there is no other combination of prime numbers that can be multiplied to make 60. All other combinations (for example, 2 x 3 x 3 x 3 = 54 and 17 x 2 x 2 = 68) give
products other than 60.
4. Mei Ling would end up with 1 x 60, 2 x 30, 3 x 20, 4 x 15, 5 x 12, and 6 x 10. After that, she would be repeating factors (for example, 10 x 6). So the
factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
Hine would end up with:
2 x 2 x 3 x 5 = 60
2 x (2 x 3 x 5) = 2 x 30
3 x (2 x 2 x 5) = 3 x 20
(2 x 2) x (3 x 5) = 4 x 15
5 x (2 x 2 x 3) = 5 x 12
(2 x 3) x (2 x 5) = 6 x 10
From these, she would get the same factors of 60 as Mei Ling. (Although 1 is not a prime factor, Hine would need to include 1 as a factor to balance the 60 from 2 x 2 x 3 x 5, which is 1 x 60.)