What to Do?

This activity encourages students to represent word problems as box diagrams and equations. Some educators refer to this as “mathematising”. Research indicates that students often find mathematising difficult and need considerable support to analyse the arithmetic structures involved.
Be aware that different word problems that may be represented with the same equation can vary considerably in difficulty. The easiest problems for students to represent are usually those that describe actions. “Sarah has 43 marbles and loses 18 of them. How many marbles has she got now?”
suggests an action of taking away. Students usually associate taking away with subtraction and can mathematise this as 43 – 18 = number.
However, some story problems have wording that don’t suggest an action. For example, “Kellie has 76 stamps, and Tyler has 49 stamps. How many more than Tyler does Kellie have?” does not describe an action. It describes a difference, and the students must understand what action is needed to find that difference.
Other variables that affect the difficulty of word problems are the position of the unknown and the number of steps involved in the calculation. Problems that have the unknown at the start are hardest to solve. For example, “Leighton has a lot of matchbox cars. After opening his birthday presents, he has 48 cars. That’s 3 times as many cars as he had before. How many cars did he have before his
birthday?” Start-unknown problems are tricky because the student has to reverse the operation to solve them. In this example, the student needs to reverse “3 times as many”, that is, reversex 3 = 48 to become 48 ÷ 3 =.
Multiple-step problems are always harder to solve than single-step problems of the same kind because there are more pieces of information to organise and store during the calculation. The students need to be taught recording strategies that will help them to organise and store the important information in the problems they are trying to solve.
Box diagrams are powerful representations for a range of problems. The students need to be as accurate as possible with the ratios they allocate to each part of their diagram. Using square grid paper can help with this. Once the students have drawn a box diagram for any of the problems in this activity, get them to check that it matches the information. For example, suppose the students have presented the following diagram for question 5:

Alana, Brenda, Caleb, and Donald are the same age. Are the boxes for their ages the same size? The 52 candles show their combined age on their next birthday. Do you have a single box labelled 52 that matches the total length of all four children’s ages?
How will you work out what each box showing the children’s ages is worth?
How old are the children now?
From the box diagram, the students will find it easier to solve the problem by operating on numbers, in this case, 52 ÷ 4. The catch in this question is “How old are they now?” 52 ÷ 4 gives 13 as their age on their next birthday, so they are 12 now.
The problems in questions 3–8 become increasingly complex because they involve inactive language and more calculation steps. For example, consider a possible box diagram sequence for question 8:

Representing the box diagram as a calculation requires algebraic reasoning. The diagram shows that there are 3 unknowns of the same size, labelled “?”, that represent the number of people in the front carriage. So the equation is (3 x ) + 11 = 38. The students might solve this by trial and improvement. Putting 10 as the unknown gives 3 x 10 + 11 = 41, which is too large. By adjusting the unknown value, the students will find the correct number, 9. Some students may recognise
that the problem can be solved using inverse operations: 3 x  + 11 = 38 so 3 x  = 27 so  = 9 in the front carriage. This shows a structural understanding of the operations involved. Another way of solving this is shown in the Answers.

Extension

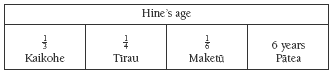
Extend the use of box diagrams to problems involving fractions, ratios, and proportions. For example, “Hine has lived one-third of her life in Kaikohe, one-quarter of it in Tìrau, one-sixth of it in Maketū, and the other 6 years in Pātea. How old is Hine?”
An initial box diagram of the problem might look like this:

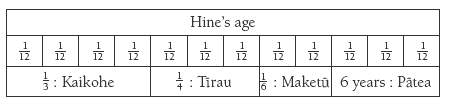
Then:

From this , it can be seen that 6 years = 3/12. 1/12 is therefore 6÷ 3 = 2 years, so Hine mustbe 12 x 2 = 24 years old.

You can also work out Hine's age by using equations:

1/3 + 1/4 + 1/6 = 4/12 + 3/12 + 2/12 = 9/12.

So 6 years is 12/12 - 9 /12 = 3/12.  6 years is 3/12, so 1/12 is 6÷ 3 = 2 years, so Hine must be 12 x 2 = 24 years.

More difficult problems often involve change. For example, “Brad has twice as much money as Leah has. He spends $45. Now he has half as much money as Leah has. How much money does Leah have?” Box diagrams are a good way to show this problem:

Answers to Activity

1. 1 403 – 874 = . Felise needs 529 more stamps.
2. a. Diagram i shows Asosi’s problem. He took out $986 and had $1,309 left, so his original amount was $986 + $1,309.
b. $2,295. (986 + 1 309)
3. Possible equations and their answers are:
Number of plums = 7 x 39
7 x 39 = 273
or:
Number of plums = (7 x 40) – 7
(7 x 40) – 7 = 280 – 7
= 273
4.  x 24 = 864
or  = 864 ÷ 24
= 36 cartons
5. = 52 ÷ 4 = 13 years. So they are now 12 years old.
A possible box diagram of this problem is:

6.  = 756 ÷ 9 = 84 cards
A possible box diagram of this problem is:

7. 1 248 ÷ 3 = 416, so Sophie has 416, and Chris has 2 x 416 = 832.
A possible box diagram of this problem is:

8. 9 in the front carriage, 12 in the middle carriage, and 17 in the last carriage.
One way to solve this is:
There are 38 passengers altogether.
Last = front + 8
Middle = front + 3 (or = front + 8 – 5)
Front = (38 – 8 – 3) ÷ 3
= 9
(So the last carriage has 9 + 8 = 17, and the middle carriage has 17 – 5 = 12 or 9 + 3 = 12.)