The Unit Fraction Game

Game and Activity

The game and activity on this page can be used to improve your students’ understanding of fractions, in particular, their understanding that fractions can function both as numbers and as operators. It can also be used to improve their confi dence when it comes to adding, multiplying, and simplifying fractions.
In the game, the students must toss a pair of dice. One dice gives a number, and the other dice gives an operation to perform on that number. Probability concerns the chance of a particular outcome occurring in relation to all the possible outcomes (in this case, 36) that might occur in a given situation.
Check that the students:
• understand unit fractions and mixed numbers (this is vital for this exercise);
• recognise equivalent fractions (for example, that 1/2 + 1/2 = 2/2 or 1);
• know that fractions can operate on other numbers multiplicatively (for example, they can find 1/4 of another number);
• know that, when adding fractions with the same denominator, the denominator stays the same (for example, 1/4 + 1/4 = 2/4 or 1/2);
• know that, when adding fractions with unrelated denominators (that is, when one
denominator is not a multiple of the other), the fractions need to be rewritten as equivalent fractions with a common denominator (for example, 1/3 + 1/4 = 4/12 + 3/
12);
• know their multiplication facts and how to multiply unit fractions with whole numbers.
Like a number of the other activities in this book that involve probability, this activity explores the notions of fairness and variability.
Whether the game is fair could be tested by playing it a large number of times. But, as question 2 is designed to clarify, three games is definitely not a large number: three losses from three trials means nothing. There is, however, only one certain way of showing whether the game is fair, and that is by listing all the possible outcomes and seeing whether an equal number favour each player.
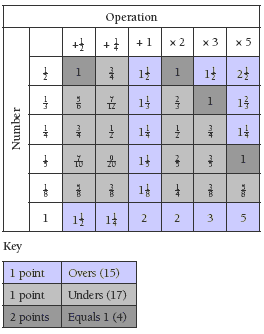
All 6 sides of the two dice are equally likely to appear face-up after being thrown, and any one side of the first dice can appear with any of the 6 sides of the second dice, so there are 6 × 6 possible outcomes. These are set out as a table in the Answers.

Answers to Activities

Game
A game to improve your ability to operate with fractions
Activity
1. “Not fair”, in a situation like this, means that the chance of losing is greater than the chance of winning.
2. While it might suggest that the chance of losing is greater than the chance of winning, it doesn’t actually prove anything. (The cause might just be a run of bad luck.)
3. Comments will vary, depending on your experience of the game.
4. a. Methods will vary. Here is one:
Each of the 6 operations can be carried out on each of the 6 numbers. That’s
a total of 6 × 6 = 36 possible results. These can be set out as an array or table,
like this:

This table shows that 17 of the possible outcomes are unders and 15 are overs. So the “unders” player has slightly more chance of scoring a point than the “overs” player.
b. If you were to play a large number of games, you should fi nd that the game is biased slightly in favour of the “unders” player. Explanations will vary but could be similar to that given in 4a.

Key Competencies

The Unit Fraction Game can be used to develop these key competencies:
• thinking
• managing self