This problem solving activity has an algebra focus.
Triangular numbers are made by forming triangular patterns with counters.
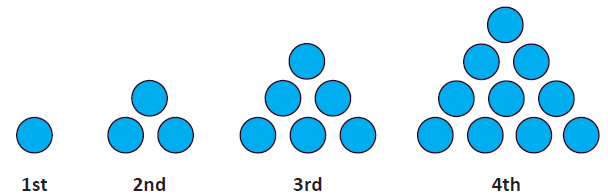
Riwa has made the first four triangular numbers with blue counters.
Riwa didn’t think that the first triangular number really looked like a triangle but it seemed a good place for the pattern to start.
The first triangular number is made with just one counter and so is one.
The second triangular number is 3.
The 3rd triangular number is 6 and the 4th triangular number is 10.
What is the 10th triangular number?
What is the 20th triangular number?
- Continue a pattern.
- Use a table where appropriate.
- Find a relation between successive members of a pattern.
In this problem students explore and continue patterns, and describe the rule for the recurrence of a pattern. Using a table, and incorporating number properties are valuable skills that can be used in many situations.
This problem is the first of four Algebra problems relating to triangular numbers: Counting Pills, Level 4; Triangular and Square Numbers, Level 5; and Triangular Number Links, Level 6 (Number and Algebra - Equations and Expressions). These problems develop the idea of the triangular numbers leading to an algebraic formula for the nth triangular number.
This problem is also related to the Level 3 Algebra problems Building Patterns Incrementally and Building Patterns Constantly.
The Problem
Triangular numbers are made by forming triangular patterns with counters. Riwa has made the first four triangular numbers with blue counters.
Riwa didn’t think that the first triangular number really looked like a triangle but it seemed a good place for the pattern to start. The first triangular number is made with just one counter and so is one. The second triangular number is 3. The 3rd triangular number is 6 and the 4th triangular number is 10.
What is the 10th triangular number?
What is the 20th triangular number?
Teaching Sequence
- Introduce the problem to the class. Brainstorm ideas for approaching the problem and keeping track of what has been done (e.g. by using a table).
- As the students work on the problem in pairs you might ask the following questions to extend their thinking:
What strategies might help you to find the answer?
How can you use your knowledge about numbers here?
Can you see any patterns that might help? Could you write an expression that demonstrates this? - Share the students’ answers. Ask them to explain their reasoning.
- Ask students to write up their method of solution.
- Use the extension problem for students ready for extension or as a problem on another day.
Extension
Which triangular number is equal to 120?
Solution
Many students will add new rows of counters, and make the 6th, 7th, 8th, 9th and 10th triangular numbers by construction. They will find that each new row requires one more counter than the previous one. This should lead them to see that the 10thtriangular number is the 4thtriangular number plus 5 + 6 + 7 + 8 + 9 + 10. That is, 10 + 5 + 6 + 7 + 8 + 9 + 10. These can be added in order to give the 10th triangular number as 55.
They may also see that the 1st triangular number has one on the bottom, the 2nd two on the bottom, the 3rd three and so on. The 4th triangular number is made up of 1 + 2 + 3 + 4 counters. So the result for the 10th triangular number can be written as 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10.
There is a quick way to add consecutive numbers like this (see Algebra Information). When a string of numbers like this are added it is useful to ask yourself whether adding them in a different order makes the task more interesting. In this case, since the students will be familiar with ‘making ten’, it is natural for them to suggest adding (1+ 9) + (2 + 8) + (3 + 7) + (4 + 6) leaving only 5 and 10 to be added later. So, the 10th triangular number is 10 + 10 + 10 + 10 + 5 + 10.
Another interesting way of adding the numbers is to add the first and the last, then the second and the second to last, and so on. This leads to (1+ 10) + (2 + 9) + (3+ 8) + (4 + 7) + (5 + 6). This simplifies to 11 + 11 + 11 + 11 + 11 = 55.
Encourage the students to think like this when they work out the 20th triangular number. So they have to add 1 + 2 + 3 + … + 20 = (1 + 20) + (2 + 19) + … + (10 + 11) = 10 x 21 = 210.
Solution to the Extension
If there are 120 counters, which triangular number do they make? One approach is to take 120 counters and make up a triangle. The number of the counters in the bottom row is the number of the triangular number.
A more efficient strategy is to guess that it is the 12th triangular number. By using what has already been done, students might recognise that it must be between the 10th and the 20th triangular number. Checking with the method above shows that the 12th triangular number is 78. This is still not enough so try again.
Drawing a table, building on what is already known, shows this.
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 55 | 66 | 78 | 91 | 105 | 120 | … |
The 15th triangular number has 120 counters.
Consider also representing triangular numbers in the shape of a staircase.