Tiling Spacecraft

In this activity, students use different approaches to finding a rule for a practical situation.
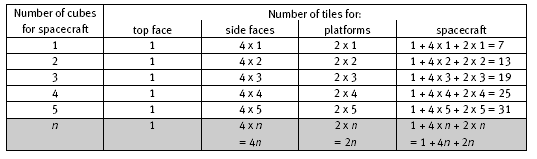
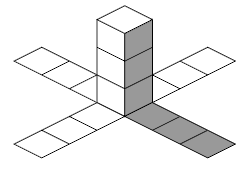
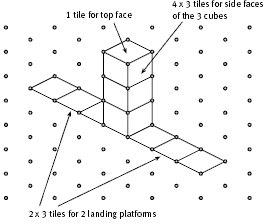
In question 1a, the students must interpret 1 + 4 x 3 + 2 x 3 as being the number of tiles for a 3-cube spacecraft. There is 1 tile for the top face, 4 x 3 tiles for the side faces of the 3 cubes, and 2 x 3 tiles for the 2 landing platforms. (See the diagram in the Answers.) They draw this spacecraft on isometric dot paper. This task is likely to focus their attention on the three different tile positions: the top, sides, and landing platforms. This should help them see how Jeff’s rule arises.
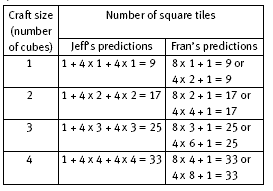
The following table shows how Jeff’s short cut leads to his rule:

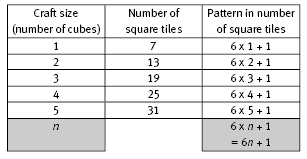
Fran uses an alternative approach in question 3. She doesn’t separate tiles for the top face from the tiles for the side faces and the tiles for the landing platforms as Jeff has. She gets the total number of tiles for spacecraft of different sizes and then looks for a pattern. Her rule, 6 x n + 1 or 6n + 1 is probably based on the fact that the number of tiles increases by 6 for each cube added.

Note that, although the rules are different, Jeff’s rule simplifies to 6n + 1, which is the same as Fran’s rule.
In question 4, the rules change in that there are 4 landing platforms instead of 2 as in questions 1 to 3. Jeff adjusts his rule to allow for the 2 extra landing platforms, while Fran may again look for a direct relationship between the number of cubes and the number of tiles.
Alternatively, Fran might recognise that we can consider each vertical face of the spacecraft together with its associated landing platform.

So, for example, in the 3-cube spacecraft, there are 4 lots of 6 tiles plus 1 tile on top, so the calculation is 4 x 6 + 1. In general, for n cubes there are 4 x 2n + 1 tiles. The rules that develop from the short-cut table shown in the Answers are:

As with the previous two rules, Jeff’s rule simplifies to Fran’s rule, 8n + 1.
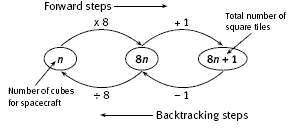
In question 4d, the students must work backwards to calculate the number of cubes in a spacecraft with 193 tiles. They will find that using Fran’s rule, 8n + 1, provides the most straightforward approach. This backtracking flow chart shows how the rule 8n + 1 and its reverse work.

Answers to Activity

1a.

b. 1 + 5 x 4 + 2 x 5 = 31 square tiles. The drawing will have 2 more cubes and 2 more tiles on each landing platform than the one in a.
2. In the rule 1 + 4 x n + 2 x n, the letter n stands for any number of cubes that make up the body of the spacecraft. For example, when n = 5, the spacecraft
looks like 5 stacked cubes. There will be 1 square tile on the top face and 4 square tiles on the side faces of each of the 5 cubes, that is, 1 + 4 x 5 tiles.
Each of the 2 landing platforms has 5 square tiles, so there are 2 x 5 square tiles for the landing platforms. So a 5-cube spacecraft has 1 + 4 x 5 + 2 x 5 square tiles.
A 10-cube spacecraft has 1 + 4 x 10 + 2 x 10 square tiles, and a 100-cube spacecraft has 1 + 4 x 100 + 2 x 100 square tiles. In general, a spacecraft with any number (n) of stacked cubes will have 1 + 4n + 2n square tiles.

3a.

b. Fran notices that the number of square tiles is 1 more than 6 times the number of cubes. So for any number (n) of stacked cubes, there are 6 x n + 1 or 6n + 1 square tiles.

4a.

b. Jeff’s rule is: the number of tiles on the top face (1) plus the number of tiles on the 4 side faces of each cube multiplied by the number of cubes plus the number of landing platforms multiplied by the number of tiles on each platform (4). If n stands for the number of cubes for the spacecraft, then the number of square tiles in
Jeff’s rule is 1 + 4 x n + 4 x n or 1 + 4n + 4n.

Two possible rules for Fran are: the number of square tiles is 1 more than 8 times the number of cubes, or the number of square tiles is 1 more than 4 times twice the number of cubes. So for any number (n) of stacked cubes, there are 8 x n + 1 or 4 x 2n + 1 square tiles.
c. For a 100-cube spacecraft, n = 100. So using Jeff’s rule:
1 + 4 x n + 4 x n
= 1 + 4 x 100 + 4 x 100
= 1 + 400 + 400
= 801 (the number of square tiles)
and using Fran’s rules:
8 x n + 1
= 8 x 100 + 1
= 801 (the number of square tiles)
or
4 x 2n + 1
= 4 x 200 + 1
= 801
d. Fran’s first rule indicates that the number of square tiles, 193, is 8 times the number of cubes plus 1. 8 times the number of cubes equals 192, and the number of cubes is 192 ÷ 8 = 24. So the spacecraft is a 24-cube spacecraft.