Ratios

Session 1

In this session we introduce students to the concept of a ratio and ways that it can be expressed.

1. Show the students a bottle of drink concentrate and read the instructions on the label on how to make the drink. For example, some bottle labels say "Makes 5 litres" or mix 1 part concentrate to 4 parts water. Either create a mix with real concentrate or water or use Slide 1 of PowerPoint 1 to demonstrate.
2. Use Slide 2 to write the recipe as a ratio such as 1:4 and explain to the students that 1:4 refers to 1 part of concentrate for every 4 parts of water. “Per” is a word commonly used to mean “for every.” Ask the students why they think we use the term “parts” rather than giving specific amount in millilitres. A ratio remains consistent, no matter the amount of liquid it applies to, e.g., 1 mL concentrate to 4 mL water is the same ratio as 1 L of concentrate to 4 L of water.
3. Discuss what fractions they can see in the ratio. Express the part to whole relationship as fractions: 1/5 concentrate to 4/5 water (Use Slide 2). Also show how the part-whole fractions can be renamed as equivalent fractions and percentages (Slide 3). 
4. Provide 2:8 as another example of a concentrate to water ratio. Mix the ratio up in a different plastic cup to 1:4.  
   Which ratio 1:4 or 2:8 will have the strongest taste? How do you know? 
   Let students discuss their ideas. Look for common incorrect ideas, such as: 
   2:8 has more concentrate so it will taste stronger than 1:4.  
   2:8 has more water so it will taste weaker than 1:4. 
   Let a few students taste-test the mixtures. They should conclude that the mixtures taste the same. Use Slides 5-7 to show that 2:8 has the same part whole relationships as 1:4 since 1/5 = 2/10 and 4/5 = 8/10.
5. Ask students to work in pairs. They will need some concentrate and water, a couple of plastic cups and a way to measure small quantities. While eye droppers are ideal, pipetting with plastic straws makes a good substitute. Use Copymaster One to provide each pair of students with a card showing two ratios. Make sure the cups are labelled with the ratio of mixture they hold.
6. Allow students time to create their mixtures then taste test to establish the relative strength of flavour. Gather the class and attempt to order the ratios using the results from the groups. Use Slide 8 as a prompt. 
   Is it possible to know that some ratios are stronger than others, without tasting? 
   Students might suggest several pairings:

• 3:5 is stronger than 6:11 because doubling 3:5 gives 6:10 which has less water 6:11.
• 5:9 is weaker then 2:3 because tripling 2:3 gives 6:9 which has more concentrate of the same amount of water.
• 5:9 is stronger than 6:11 because it has only 4 more water parts than concentrate compared to 5 more 6:11 (Flawed reasoning)
• Doubling 3:5 gives 6:10 and tripling 2:3 gives 6:9 so 2:3 is stronger as it has less water.

7. Use slides 8-10 to work with students to order the ratios by strength of taste. Calculators can be used to convert the part-whole relationship of parts of concentrate to total number of parts, e.g., 2:3 is 2/5 concentrate. Similarly,
8. Slide 10 shows the ratios in taste order from weakest to strongest. Several true or false statements are posed. Only the last statement is true. Use the established order to check the statements.
9. As an exit question, pose the following problem (see Slide 11): 
    
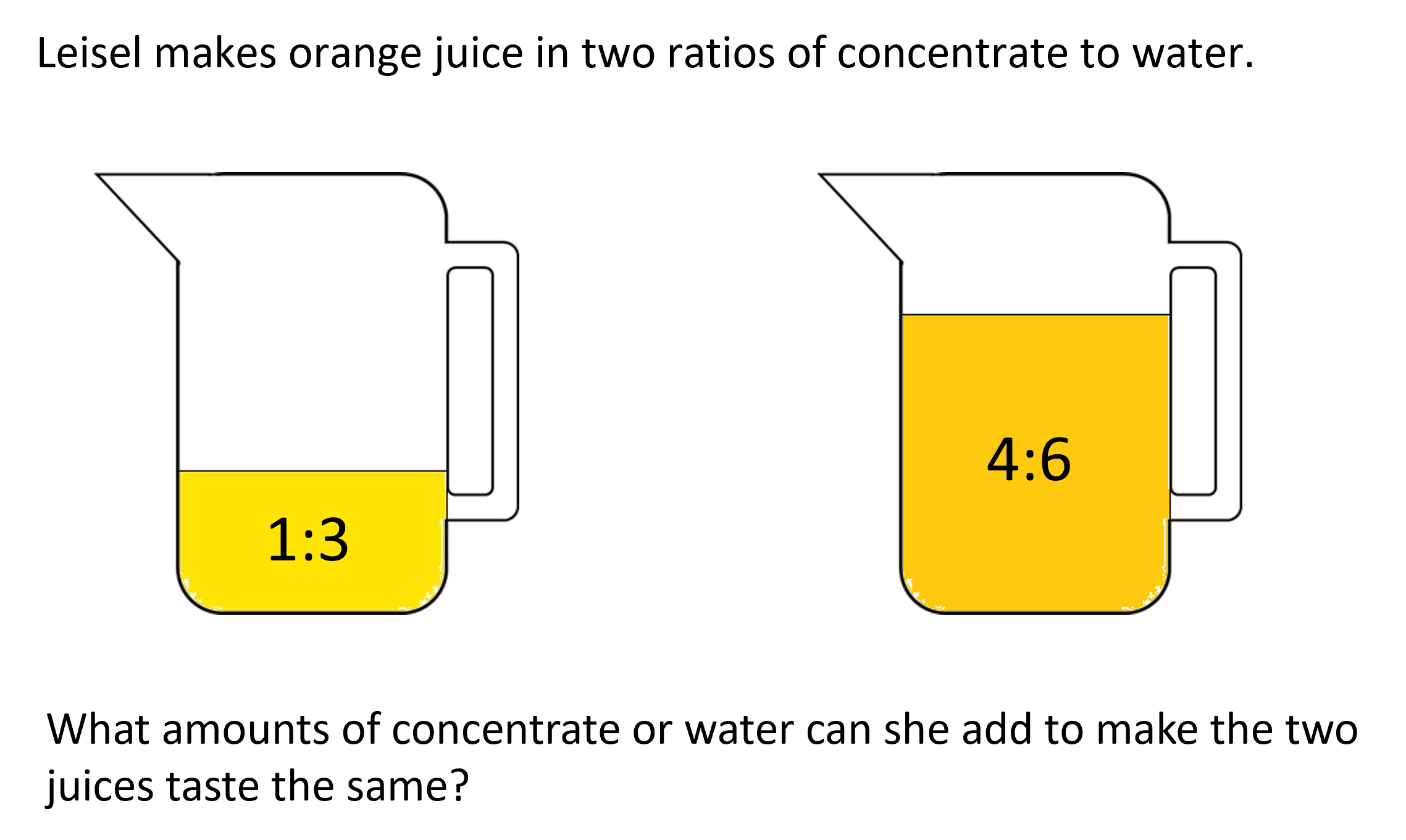
   Ask students to post their answer and name into a container upon exit. Use the answers to quickly review who understands ratios from the lesson. 
   If Leisel adds 1 part of concentrate to 1:3 to make 2:3, it will taste the same as 4:6.

Session 2

In this session students compare ratios by converting between ratios, fractions, and percentages.

1. Use PowerPoint Two to recap on the previous lesson about comparing concentrate to water ratios by taste. Begin with the problem on slide 1. Make up each ratio using concentrate and water, using an eyedropper or large straw to measure the parts. Label the mixtures and save them as a check of students’ solutions. 
   
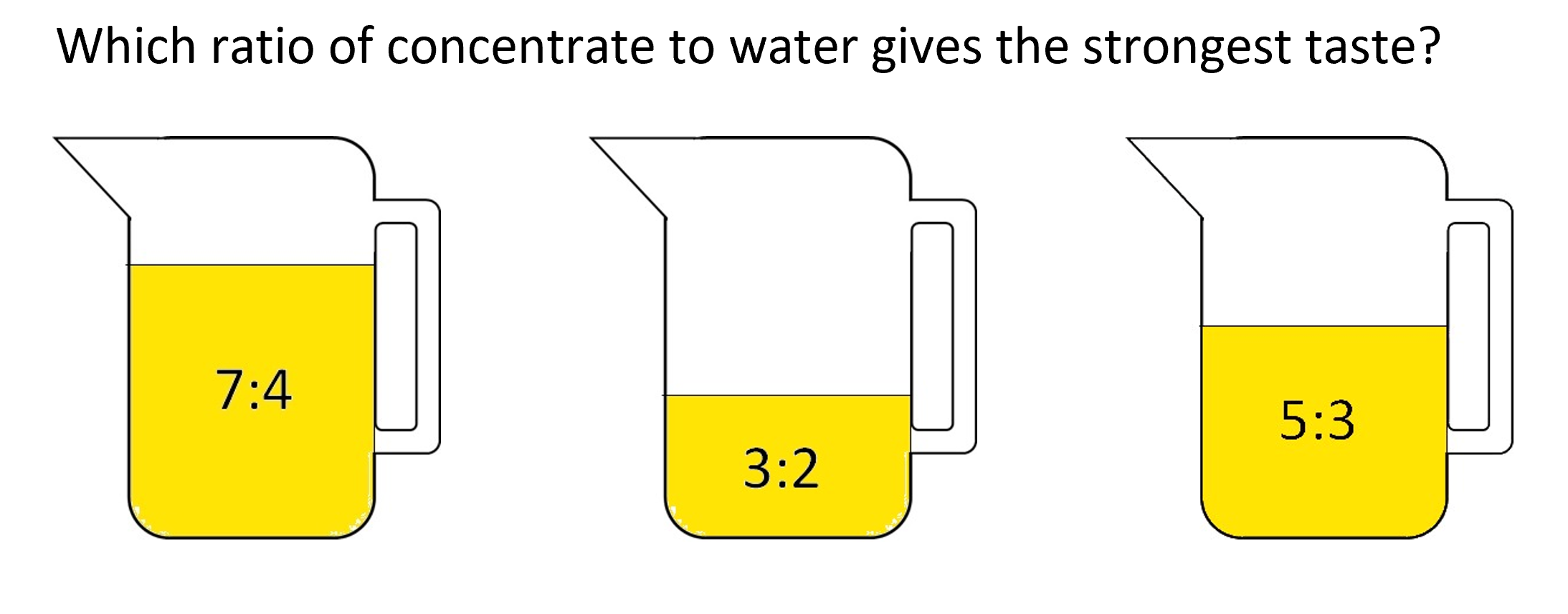
2. Let students work on the problem in pairs or threes. Roam as they work. Look for the following:
   • Do students recognise the ratio as a relationship of parts?
   • Are they immune to common misconceptions, such as number of parts of concentrate determining strength of taste, or difference between the numbers as determining strength or weakness?
   • Can they express the part-whole relationships as fractions and percentages?
3. Gather the class to share answers. Use slides 2-4 to guide discussion. Slide 2 looks at the part-whole fractions. Consider ways to compare the concentrate to total fractions, such as:
   How big are the fraction compared to one half? (All 3 fractions are greater than ½)
   How much greater than one half is each fraction? (3/5 is ½ of 1/5 greater, 7/11 is 1 ½ of 1/11 greater, and 5/8 is 1/8 greater).
   Could we convert the fractions to equivalent fractions with common denominators? (3/5 = 33/55 and 7/11 = 35/55 so 7/11 is greater, 7/11 = 56/88 and 5/8 = 55/88 so 7/11 is greater)
4. Slide 3 shows conversion of each part-whole ratio to percentages. Ask students who used percentages to compare the ratios to show others how they use their calculator to convert. Show students how to use the fraction and S↔D buttons to convert fractions to decimals.
5. Taste-test the juices made earlier to confirm the order by strength of taste.
6. Provide students with Copymaster Two to work on in pairs or threes. Roam as they work, looking for:
   • Do students convert the ratios into part-whole fractions?
   • Do they compare the fractions using benchmark fractions or common denominators?
   • Do they use their calculators to convert the part-whole fractions to decimals and percentages, with awareness of size of the results?
7. After an appropriate time, gather the class to share answers, as follows:
   1:2 has the same strength as 3:6 given both part-whole fractions equal ½.
   3:3 is weaker than 5:4 since ½ is less than 5/9.
   4:6 is 2:3 so 2/5 concentrate while 1:2 is 1/3 concentrate. 2/5 is greater than 1/3.
   3:5 is 3/8 concentrate and 4:6 is 4/10 concentrate. 3/8 is less than 4/10 so 4:6 is stronger.
   2:6 is 1:3 so is stronger than 1:4 since there is less water for the same amount of concentrate.
   3:4 is 3/7 concentrate or 42.86% while 5:7 is 5/12 concentrate or 41.67%. So, 3/7 is slightly stronger.
   8:5 is stronger than 3:2 since 8/13 = 61.54% while 3/5 = 60%.
   7:3 = 0.7 or 70% concentrate while 5:2 = 0.7143 or 71.43%. So, %:2 is slightly stronger.
8. Let students share their own ratio comparison problems and solve them together as a class.
9. Pose the following exit problem for students (See Slide 5). 
   
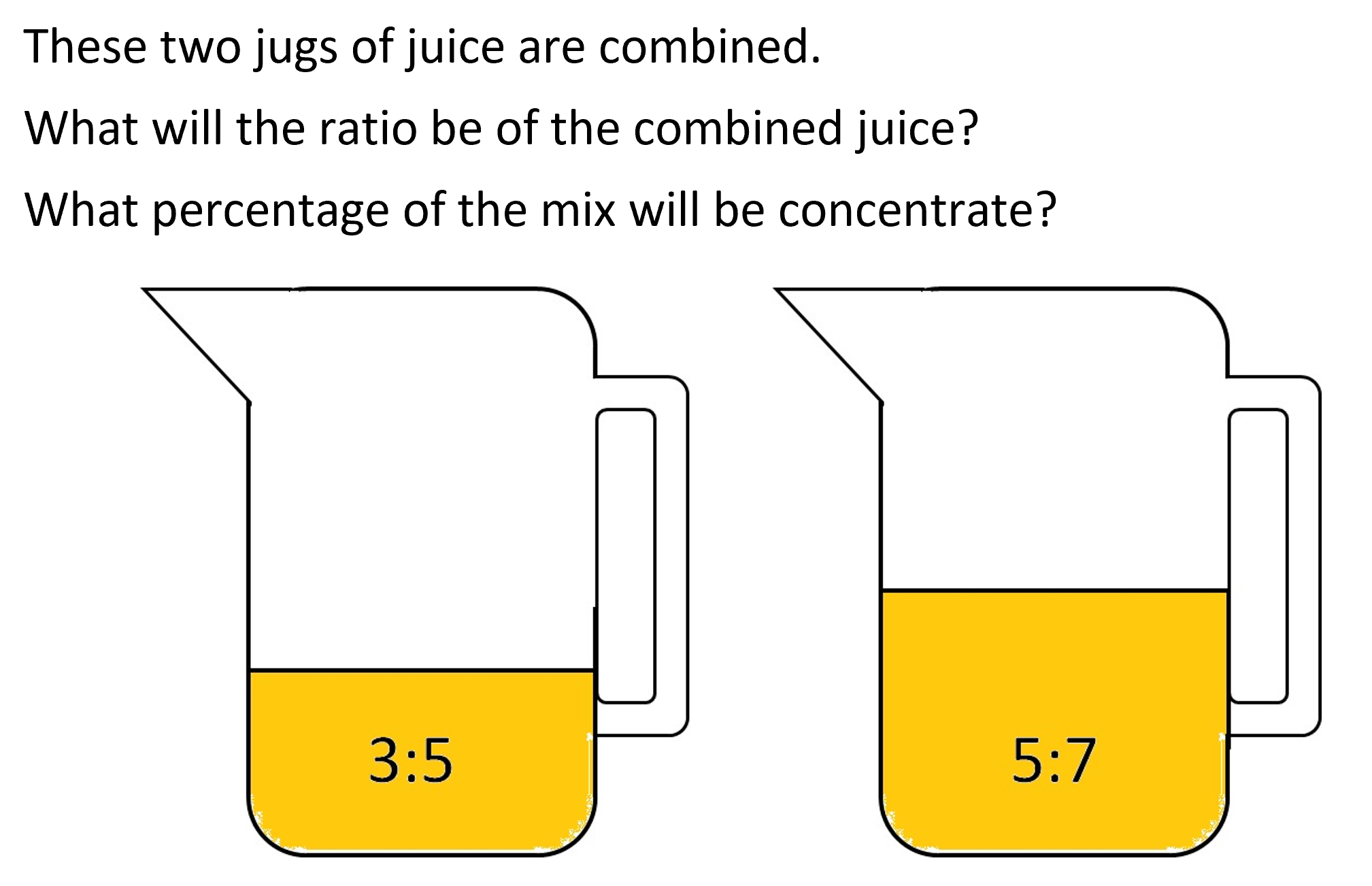
   The mix will be 8:12 which is 8/20 or 2/5 concentrate. That is 40%.

Session 3

In this session students solve problems that involve using the ratios to find the proportions in millilitres and litres. Students also investigate making changes to quantities and ratios.

1. You need to mix 2 litres of orange juice using a ratio of concentrate to water of 1:4.
   How much concentrate and water do you put in the bowl?
2. Let students discuss the problem. You may need to revisit measure units for capacity, so students know that 1 litre equals 1,000 millilitres so 2 litres equals 2,000 millilitres. Ensure students know the symbols for measurement units, L and mL.
3. Process students’ ideas possibly using Slide 2 to illustrate how the problem might be represented as a diagram. Look at calculations, like 20% of 2000 = 400 mL of 1/5 x 2000 = 400 mL, as ways to solve the problem.
4. Use Slides 4-11 to make problem cards. Arrange the cards around the room as stations. Invite the students to work in small groups and attend each station. Ask them to record their answers and working so they can share their strategies with the class later. Roam as students work. Look for the following:

• Do they identify the information that is given?
• Do they recognise what must be found?
• Do they turn the information into symbolic or diagrammatic representation?
• Do they choose correct operations to find the missing amounts?

5. After a suitable time, gather the class to discuss answers and strategies. Highlight effective ways to record, such as: 
    
   
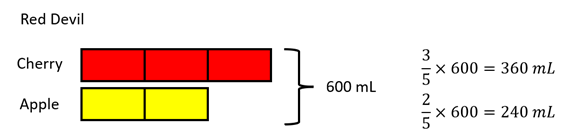
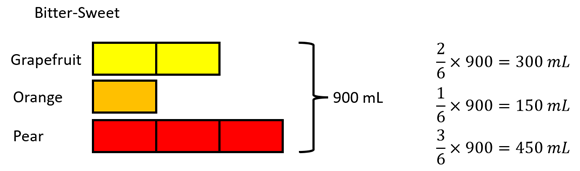
6. Answers are:
   Red Devil: 360 mL cherry juice and 240 mL apple juice
   Sour Puss: 625 mL orange juice and 375 mL lime juice
   Green with envy: 225 mL kiwifruit juice, 135 mL grape juice, and 90 mL peach juice
   Traffic light: 225 mL kiwifruit juice, 225 mL orange juice, and 300 mL apple juice
   Pearfect: 900 mL pear juice, 450 mL peach juice, and 150 mL grape juice
   Pom-Bomb: 180 mL pomegranate juice, 90 mL cherry juice, and 90 mL apple juice
   Bitter-Sweet: 300 mL grapefruit juice, 150 mL orange juice, and 450 mL pear juice
   Kiwi Cure: 800 mL kiwifruit juice, 600 mL lime juice, and 400 mL peach juice
7. Give the students the following exit problem (See Slide 12) to check their understanding of ratios:
   The bartender mixes 100 mL of lime juice with 400 mL of apple juice and 200 mL of grape juice.
   How much mix does he make?
   What percentage of the mix is each juice, lime, apple and grape?
   What is the cocktail called?

Session 4

In this session students solve problems by reducing ratios to simplest form. That requires them to look for common factors in the amounts given for each ingredient.

1. Use Slide 1 of PowerPoint Four to pose this problem.
   Citrus, the bartender, experimented with new mocktail recipes.
   His record keeping was excellent so he could recreate each successful recipe.
   However, to enter the mocktail competition he needs to record his recipes like this:
   X parts ingredient A
   Y parts Ingredient B
   Z parts ingredient C
   etc.
   Slide 2 presents 3 recipes for students to work on. The goal is to represent each recipe as a simple ratio.
2. Let students work on the recipes. Look for diagrammatic and symbolic representations. After a suitable time gather the class and use Slides 3-5 to discuss their answers. Note that students are likely to use smaller common factors first. Successive use of small factors leads to simplest form, it just takes more steps. For example:
   
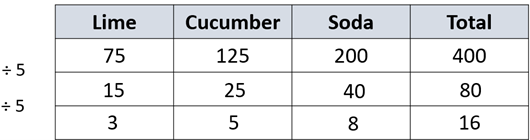
   Slide 5 shows a solution of 3:9:15.
   Do 3, 9 and 15 share a common factor? (Dividing all by 3 gives 1:3:5)
3. Provide the students with Copymaster 3 that contains many problems about reducing ratios to simplest form. Roam as they work to see students are dividing the measures by a common factor.
4. Gather the class to discuss answers and strategies.
   How do find the common factor if there is one? 
   This should raise divisibility ideas, such as “If all the numbers are even then two is a common factor,” and “If the numbers all have zero or five as the ones digit then five is a common factor.” Some students may know divisibility rules for three and nine (digital sum). 
   Process the answers, highlighting the use of diagrams, ratio tables, and division.
   Here is a full set of answers.
   Sweet As = 3:4:2               
   Cool As = 5:2:4 
   Citric As = 9:1:3
   Three P’s = 9:4:6
   I see red = 10:7:8 
   Crusher = 12:9:10
   7 = 5:3:2                                
   8 = 7:9:5
   9 = 27:23:31
   10 = 1:3:4
   11 = 3:4:2   
   Ratios:
   6:9:12 = 2: 3: 4  (CF of 3) 
   7:5:3 No (since 3,5, and 7 are primes)
   21:35:14 = 3:5:2 (CF of 7) 
   54:63:45 = 6:7:5 (CF of 9)
   19:31:43 No (since 19,31, and 43 are primes)   
    14:22:38 = 7:11:19
   18:27:45 = 2:3:5 (CF = 5) 
   33:18:42 = 11:6 :14 (CF = 3)
   11:13:17 No (since 11,13, and 17 are primes)   
   35:50:45 = 7:10:9
   
   How do you work out that a ratio cannot be reduced further?
   If any of the numbers are prime the ratio is non-reducible. Also, if the numbers are relatively prime (No common factor other than 1) then the ratio is non-reducible.
5. Use Slide 6 to introduce this exit problem. Students will need at least 5 minutes to work on it before submitting their answers.
   

Session 5

In this lesson students solve problems that involve combining ratios. When two ratios are combined the different measures need to be combined separately.

1. Use Slide 1 of PowerPoint 5 to explain the following problem to students and work with them to solve it. 
   There are 30 students in Room 1.  Each student votes for their favourite drink for morning break.
   10 students vote for fruit juice and 20 students vote for flavoured milk. 
   How can this result be expressed as a ratio? (10:20 = 1:2 in simplest terms)
2. (Slide 2) 
   There are only 25 students in Room 2. 
   10 students vote for fruit juice and 15 students vote for flavoured milk. 
   How can this result be expressed as a ratio? (10:15 = 2:3 in simplest terms)
3. (Slide 3) Leila and Harry have different ideas about what happens when the two ratios are combined.
   Discuss who is right and why they are right?
    
   Students should recognise that both students are correct to some extent. Adding the measures is necessary but it is unwise to add the reduced ratios as Harry has done. That is because the reduced ratios have different weightings since there are different numbers of students in each class. Leila’s idea is best. 20:35 = 4:7 in simplest form. Animate Slide 4 to show how that works.
4. Give the students problems to solve that involve combining ratios. Here are some examples of problem structures you can use to develop problems to ask students:
   • Slide 5
     John and Rangi bought bottles of soda water and juice for the class party. 
     John bought 5 bottles, 2 bottles of soda water and 3 bottles of juice. 
     Rangi bought 10 bottles of soda water and juice in the ratio of 3:2. 
     If John and Rangi combined their bottles together to make punch what is the new ratio of soda water to juice? 
     (Answer = 8:7)
   • Slide 6
     Hine made fruit punch using ginger ale and juice in the ratio of 3:2. 
     Amy made her fruit punch in the ratio of 2:5 but she made half as much. 
     When the girls combined their punch in a bowl what is the ratio of ginger ale to juice? 
     (Answer = 8:9)
   • Slide 7
     For camping trip one family brought 8 bottles of drink, 1/4 of the bottles were apple juice and the rest were water. 
     The second family brought 7 bottles, 3 of them were apple juice and 4 were water. 
     When the two families combined all the bottle what was the ratio of apple juice to water? (Answer = 1:2)
5. Provide the students with Copymaster 4 that contains further problems about combining ratios.
   Answers are:
   • 2:3
   • Bus 2 has twice as many passengers as Bus 1. There are many solutions such as Bus 1 with 5 students and Bus 2 with 10 students, Bus 1 with 10 students and Bus 2 with 20 students, etc.
   • The larger bag has twice many marbles as the smaller bag, 100 marbles.
   • The number of fish in the tank must be a multiple of 5 greater or equal to 10, in order to get a ratio of 1:5 after guppies are removed. The number of non-guppies, at first, must be a multiple of five. Some answers:
     25 fish at first then remove 7 guppies, 50 fish at first then remove 14 guppies, etc.