Non-stop Ninths

In this activity, the students investigate non-terminating decimals. There are two kinds of nonterminating decimals:
• recurring, non-terminating decimals, in which digits repeat, such as = 0.333333… or 1/11 = 0.090909…, and which can be renamed as common fractions;
• non-recurring, non-terminating decimals, in which the digits do not repeat, such as
√2 = 1.4142135… and π = 3.14159… These numbers cannot be renamed as common fractions and are known as irrational numbers.
Recurring decimals can be shown by a dot over the repeating digit, for example, (which is 0.333…) or (which is 0.1666…) or over the first and last of the repeating digits, for example, (which is 0.090909…) or (which is 4.53210621062…). Sometimes a line is used to show the recurring pattern, for example, 0.090909...can be shown as . Usually, a recurring decimal must be rounded before it can be used in a calculation. This is shown by indicating the
number of decimal places that the number was rounded to. For example:
2/3 = 0.666…
= 0.667 (3 d.p.)
= 0.7 (1 d.p.)
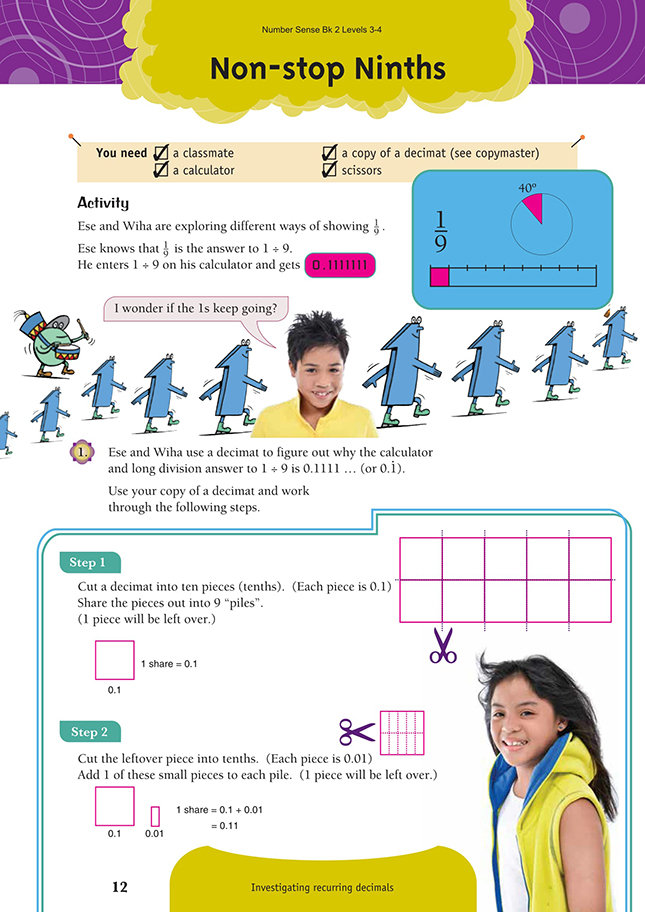
Students usually first encounter recurring decimals when they are dividing by 3 or by multiples of 3. In the first part of this activity, the students gain practical experience in recurring decimals involving ninths. They will probably have used decimats when exploring the meaning of fractions. (See decimat copymaster at the end of these notes.) In those instances, a convenient cut or two would probably have been enough to divide the whole into its fractional parts. In question 1 of this activity, the decimal system means there are no convenient cuts that can be made to model the division of a whole (decimat) into 9 equal parts. Instead, the students divide the whole into
10 equal parts and model the division by sharing out what can be shared, dividing the remainder, and then repeating the process.
If your students are new to the concept of recurring decimals, use question 1 as a class or whole group activity. This may reduce the possibility that the students could get confused with lots of little bits of paper. Alternatively, the students could work on the problem in pairs or small groups. If you use small groups, expect everyone in the group to be able to explain clearly the meaning of the cutting they have just done. Ask questions such as:
What is the value of this (uncut) mat? (1)
Now that it has been cut into 10, what is the value of each piece? (1/10 or 0.1)
How can I start sharing the 10 pieces equally between 9 people? (Give 1 bit to each person, with 1 piece left over.)
How can I now share the leftover piece equally between the same 9 people? (Cut it into 10 equal bits and give 1 bit to each person, with 1 piece left over.)
Now that the leftover piece has been cut into 10 pieces, what is the value of each little piece? (1/10 of 1/10, which is 1/100 or 0.01)
What is the total value of the shares that the 9 people now each have? (0.1 + 0.01 = 0.11)
Does each person now have exactly 1/9 of a whole (decimat)? (No.)
Keep the focus on the size of each of the 9 shares as each little bit of decimat is added to it because the size of this share is the “answer” to the question What does 1/9 look like as a decimal? Hopefully, the students will be able to see that although it is not practicable to cut a decimat into ever-smaller pieces, the process that it models can be continued indefinitely. With each application of the process, each of the 9 shares gets closer to exactly 1/9 of the whole, but a share will never equal 1/9.
This is a difficult but fascinating idea.
When students have completed this activity, they could work in groups to create posters that demonstrate their cut decimats’ idea and explain what they have learned.
In questions 3a and 3b, the students consider rounding 0.1111 to 2 decimal places. To do this, they need to make judgments based on the number line in the students’ book and their knowledge of standard rounding procedures. (See the discussion on rounding at the start of these notes.) Question 4 also requires the students to round. Note that they can see the new prices as 1/9 off the old price or 8/9 of the old price. If necessary, they can use the number line in question 2 as a model.
The number lines in the Answers have their money values underneath the line, but either way is acceptable.
Extension
The students could use a calculator to discover which unit fractions (1/2, 1/3, 1/4 and so on) are finite and which are recurring and see if they can discover a way of predicting which is which. (The key to the prediction is the factors of the  denominator. If the only factors are 2 and/or 5, the decimal will be finite. If there are any other factors in the denominator, the decimal will be recurring. So

Answers to Activity

1. Practical activity
2. Discussion will vary. For example: “We keep getting 1 piece each and 1 piece left over that has to be divided. The decimal for 1 share goes 0.111111 … with the 1 going on forever.”
3. a. 0.11
b. 0.11
4. a. i. $1.78. (2 – 0.22)
ii. $2.67. (3 – 0.33)
iii. $3.56. (4 – 0.44)
iv. $4.44. (5 – 0.56)
v. $5.33. (6 – 0.67)
vi. $6.22. (7 – 0.78)
vii. $7.11. (8 – 0.89)
viii. $8.00. (9 – 1)
b.