This problem solving activity has a geometry focus.
How many squares can you find that have dots from this array as their corners?
- Describe the properties of a square.
- Work systematically when problem solving.
- Devise and use problem solving strategies (act it out, use equipment, draw a picture).
This problem explores the concept of "squareness". It reinforces the understanding that a square has 4 equal sides and 4 right angles. The students need to recognise that a square is not always ![]()
but may be ![]() .
.
- Copymasters of dot papers
- Copymaster of the problem (Māori)
- Copymaster of problem (English)
- 4x4 Geoboards and rubber bands or 4x4 dot paper and pencils (a digital tool could also be used - search for digital geoboard)
The Problem
How many squares can you find that have dots from this array as their corners?

Teaching Sequence
- Introduce the problem as a "treasure hunt". How many squares can be made on this board? Let the search begin!
- Ask the students, in pairs, to make a square on the Geoboard with a rubber band (or draw one on the dot paper). It can be any size and in any location. Ensure students understand that a square is a flat shape with 4 sides of equal length, and 4 interior angles of equal size. If necessary, differentiate between what a square is and isn't (by drawing or with geoboards).
- Share the squares found by the class. Notice whether the squares displayed are different (e.g. by size, location, or amount of rotation).
- Pose the problem: How many squares do you think that you can find?
- As the students work ask:
How do you know when something is a square?
What did you find out during this activity?
Are you organising your search for the squares? How? - Share answers. If there are different answers look at why this is so. Get the students to share the ways that they organised their search.
Extension
Squares in a 5x5 Geoboard or copymaster 5 x 5 dot paper
Solution
20 squares
| Size of square (in squares) | Number |
| 1x1 | 9 |
| 2x2 | 4 |
| 3x3 | 1 |
| tilted (one dot enclosed) | 4 |
| tilted (4 dots enclosed) | 2 |
Some students may notice that there is a pattern in the number of the non-tilted squares (1, 22, 32)
Solution to the extension
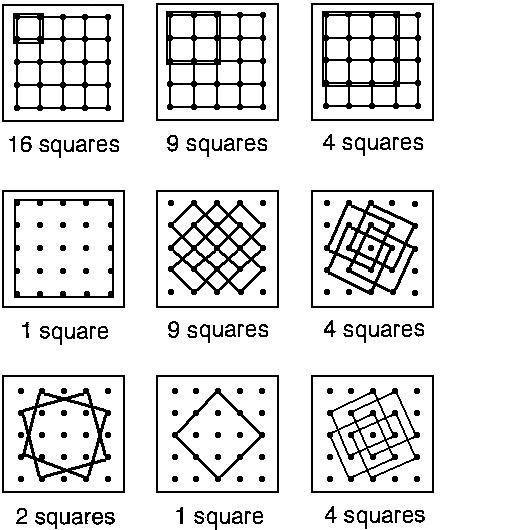
Solution to the Extension
50 squares could be made using a 5x5 Geoboard or copymaster 5 x 5 dot paper. See if you can find all of these using the system shown above.
