The Great Factor Hunt

Activity One

The “hunt” in this activity has computer spreadsheets doing the calculation work in the search for factors. It allows the students to think about the number properties involved rather than attending to the demands of calculations.
Ensure that the students understand that factors of a number, for example, 16, are whole numbers that multiply to give that number. For 16, such numbers are 1 x 16, 2 x 8, and 4 x 4.
The students also need to understand the geometric properties of a spreadsheet: the cells are designated by co-ordinates, with a vertical reference (usually a letter) and a horizontal reference (usually a number).
The spreadsheet operation may function differently with some programs, so try the activity on the class computer yourself first. For information on the use of spreadsheets, see pages 26–27, Answers and Teachers’ Notes: Algebra, Figure It Out, Level 3. Spreadsheet Challenge on pages 12–13 of Algebra, Figure it Out, Level 3 offers a supporting activity. Picking Patterns on pages 6–9 of Number
Sense and Algebraic Thinking, Figure It Out, Levels 3–4, explains how to use the Fill Down function.
Students who don’t have access to a computer could set up a spreadsheet on paper. The Fill Down function can be done manually using a calculator and a table. The students should be able to recognise the pattern: if a number is a factor, the quotient (answer) must be a whole number. (For example, if 8 is a factor of 16, the answer to 16 ÷ 8 will be a whole number. 16 ÷ 8 = 2, so 8 and 2 are factors of 16.)
Questions 1–3 reinforce this fact, that when a number is divided by one of its factors, the quotient is also a whole number. So, in general, to search for factors of a number, the students tell the computer to systematically work through dividing the number by the whole numbers from 1 to the number’s square root. Where the division gives whole number answers, both the divisor (dividing number) and the quotient (answer) are factors. The example of Trapper Tino’s search for factors of 10 on page 2 shows that for division by 1, 2, 5, and 10, the answer is a whole number. 1, 2, 5, and 10 are the whole-number factors of 10.
If the factor hunt is systematic and begins with 1 as a factor, the multiplication pairs will be listed below and above the square root of the number in question. For example, for 16, the pairs will be 1 and 16 and 2 and 8, so the list of factors will be 1, 2, 4, 8, and 16. ( 16 = 4, so 4 is also a factor.) Once the square root is reached, the search is complete. (After this, the factors simply repeat, but in the reverse order.) Be aware that for a number like 24, the square root isn’t a whole number and therefore isn’t a factor.
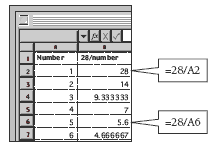
To search for the factors of 28 in question 3b, the students will need to instruct the computer to divide 28 by the numbers 1 to 28. (The computer search could stop after dividing by 6 because the square root of 28 is less than 6. It’s a good idea to allow the students to discover this for themselves.)
Setting up the spreadsheet as follows will solve the problem:

From the spreadsheet, the students can see that 1 x 28, 2 x 14, and 4 x 7 are the only pairs of factors of 28. So the list of factors of 28 is: 1, 2, 4, 7, 14, 28.
Note that for question 4, Trapper Tino could divide 203 by all of the whole numbers from 1 to 203, but because the square root of 203 is 14.24781, he only needs to use the numbers 1 to 15. On the spreadsheet that goes with this question, Tino’s search for the factors of 203 is shown to be incomplete because he has divided only by whole numbers up to 9. In fact, dividing 203 by the numbers 10 to 15 doesn’t uncover any more factors. You might expect this because 3 in the ones digit of 203 means that dividing by any even number or a multiple of 5 could not work.
That leaves 11 and 13 as the only possible whole numbers that might divide evenly into 203. They don’t!
Note: To use the square root calculator on the spreadsheet, type in =SQRT(number) in any cell. For example, to calculate √49, type in =SQRT(49).

Activity Two

This activity extends the investigations of factors. The activity will reinforce knowledge of basic facts and is a good chance to practise with divisibility tests.
When looking for factors, the students should always work systematically from least to greatest and should remember that every factor has its pair (except that in the case of square numbers, the pair is the same number, for example, in 5 x 5 = 25). If they follow this approach, they will minimise the risk of overlooking a factor. The students will probably work better in pairs. Many students will need scaffolding to help them through these investigations. You could offer this as hints enclosed in envelopes, which the students can access if they wish. On the next page are some hints
that might be useful for each investigation. The answers are in brackets. Don’t make these answers available to the students.
Question 1 focuses on prime numbers. A prime number has only two factors, 1 and the number itself. 1 is not considered to be a prime number because it only has one factor – itself. Any number that has more than two factors is called a composite number. Note that the question states that apart from 2, all prime numbers are odd. This doesn’t mean that all odd numbers apart from 1 are prime. For example, 11 is a prime number, but 33 isn’t.
Hints for question 1:
i. Even numbers can all be divided by what number? (2)
Why can’t even numbers other than 2 be prime? (Because 2 will be one of their factors)
ii. Why can’t 99, 98, 96, 95, 94, and 93 be prime numbers? (99, 96, and 93 can be divided by 3, 98 and 94 are even, and 95 has 5 as a factor.)
iii. How many factors do prime numbers have? (2 factors, 1 and themselves)
How many factors does 1 have? (1 factor, itself)
Question 2a focuses on matching pairs of factors, while 2b highlights the fact that square numbers are only listed once as a factor.
Hints for question 2:
i. The factors of a number come in pairs. For example, 1 x 24, 2 x 12, 3 x 8, and 4 x 6 give the 8 factors of 24. Does 25 have factor pairs like that? (Yes, 1 x 25 and 5 x 5, but the list of factors is {1, 5, 25}.)
ii. If you make squares with small square tiles, how many tiles does it take to make complete squares? (1, 4, 9, 16, 25, 36, and so on. These are square numbers. For example, a 5 x 5 square takes 25 tiles.)
iii. Imagine that Hunter Vaitoa Saluni used a spreadsheet to find the factors of 100. In the “divide by 10” row, the answer was 10. What does this say about 100? (100 is a square number.) Does 100 have an odd or even number of factors? (It has an odd number of factors because the 10 from 10 x 10 is listed once only as a factor.)
Hints for question 3:
i. Could the number be a prime number? Why/why not? (No. 1 + 83 = 84, and 83 is not between 50 and 70.)
ii. What kinds of numbers between 50 and 70 will have too many factors to make a total of 84? (Numbers like 54 and 64 that are multiples of 6 or 8 because they will have 2 and half of the number as one factor pair and 3 or 4 as factors as well. For example, the factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54.)
Hints for question 4:
i. The number has an odd number of factors. From question 2, what kind of a number is it? (A square number. The square numbers less than 100 are 1, 4, 9, 16, 25, 36, 49, 64, and 81.)
ii. How do you tell if a number is divisible by 3 (has 3 as a factor)? (Its digits add to a multiple of 3, for example, for 69: 6 + 9 = 15, which is a multiple of 3.) See also “Wheeling and Dealing” in this student book, which further explores 3 and 9.
There is an infinite number of factor problems that the students could come up with for question 5. To keep the maths manageable, you may find it helpful to limit the scope of the question to numbers less than 100. The students should look for a number that has several factors, and they should set a couple of constraints that are sufficient to identify it. They should then carefully check that there aren’t any other numbers that meet those same constraints. If there are, they should tighten the constraints or add a further one before giving the problem to a classmate to solve.
Some students may find it helpful to use the Sieve of Eratosthenes, which is based on finding multiples of a given number. See Material Master 8-13. Here are two possible problems that you could use as further examples:

• Two prime numbers have a sum of 120 and a difference of 14. What are they? (53 and 67)

• A number less than 100 has 6 factors, of which 4 are divisible by 5. What is the sum of the factors? (The number is 75, which has the factors {1, 3, 5, 15, 25, 75}. The factor sum is therefore 124.)

Extension

The students could find out more about the mathematical history of prime numbers. For example:
Goldbach, an eighteenth century German mathematician, declared that every even number except 2 is the sum of two prime numbers. Is this statement true?
 

Answers to Activities

Activity One
1. =10/A3
2. The numbers in column A that match whole numbers in column B are the factors of 10, that is, 1, 2, 5, and 10.
3. a. 1, 2, 3, 4, 6, 12
b. 1, 2, 4, 7, 14, 28
c. 1, 17
d. 1, 2, 3, 4, 6, 9, 12, 18, 36
4. a. 1, 7, 29, 203
b. No. Explanations will vary. Factors are always whole numbers, and none of the
numbers between 10 and 202 will divide evenly into 203. 203 ends in a 3, so if you
were trying all the numbers, you could start by eliminating all even numbers and numbers ending in 5. A quicker way is to recognise that the only factor between 2 and 9 shown on Tino’s spreadsheet is 7, which has 29 as its matching pair. 7 and 29 are both prime numbers, so you cannot double and halve, treble and third, and so on to get whole numbers that are factors of 203. For example, 7 x 2 = 14 and 29 ÷ 2 = 14.5
Activity Two
1. a. Every even number after 2 has 2 as a factor, so except for 2, even numbers can’t be prime numbers.
b. 101. (97 is the closest prime number less than 100, but 101 is closer to 100.)
c. 1 isn’t a prime number because it has only 1 factor, itself. All prime numbers have 2 factors.
2. a. Every factor has a matching “other factor”. For the number 18, 1 is matched with 18, 2 with 9, and 3 with 6. So 18 has 6 factors.
b. i. 1, 4, 9, 16, 36, 49, or the product of any number multiplied by itself
ii. Square numbers
iii. The square root of the number gives it a factor that has the same “other factor”.
For example, 64 = 8. 8 x 8 = 64, so 8 is a factor of 64. The factors of 64
are 1, 2, 4, 8, 16, 32, and 64, a total of 7 factors, which is an odd number of
factors.
3. 65. (The factors of 65 are 1, 5, 13, 65.)
4. 81. (The factors of 81 are 1, 3, 9, 27, 81.)
5. Problems will vary.