This unit explores the connections between percentages, decimals, and fractions. It focuses on strategies for solving problems involving percentages and applies these strategies to real life contexts.
- Use double number lines, ratio tables, and converting to equivalent fractions to solve percentage problems.
- Use a calculator to solve problems with percentages.
Percentages are commonly used in real life. Many of these applications involve money. So in this unit students investigate applying percentages to sales, discounts and investments.
This unit provides practice in using percentages in a range of situations and develops the link between percentages, decimals and fractions. Prior to using this unit, students should be familiar with decimals and fractions. The Level 4 units: Getting Partial to Fractions, Getting Partial to Decimals, and Getting Partial: Fractions of sets form a good foundation for the content in this unit. Getting Partial to Percentages is a parallel unit to this one. You may wish to use parts of each.
Percentages are rates out of 100 (per hundred). 50% means at a rate of 50 out of 100, a rate that is equivalent to one half. This means that 50% of a quantity (say, 40) can be calculated by multiplying the quantity by 50/100 (say, 40 x 50/100). The answer, 20, reflects the fact that 50 out of 100 and 20 out of 40 are equivalent rates, just like the fractions 50/100 and 20/40 are equivalent.
50% can be represented as an infinite number of equivalent fractions, such as 50/100 = 1/2 = 2/4 = 23/46, …. Percentages can be written as decimals, using the structure of the place value system. 50/100 also means 50 hundredths which is 5 tenths or 0.5 (note that 5 is in the tenths place). As a decimal, 50% can be represented as 0.5. Converting percentages to decimals can sometimes assist in calculation, such as 0.6 x 80 = 48 is an equivalent calculation to 60% x 80 = 48.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- beginning with commonly used percentages, such as 50%, 25%, 10%, to build up students’ fluency and confidence
- using models for recording, especially the ratio table and double number line used in the unit
- encouraging students to use a variety of recording methods to illustrate their thinking, and encouraging them to share their representations with others
- providing opportunities for students to work in mixed groupings and pairs, in which they can benefit from peer learning and scaffolding, and the sharing and justification of individual’s ideas
- providing opportunities for small group and individualised instruction that addresses specific gaps in knowledge
- providing access to calculators to allow students to confirm their estimations and experiment with more complex percentages.
The contexts for activities can be adapted to suit the interests and experiences of your students by:
- using the members of the class to create percentage problems
- creating scenarios with contexts (e.g. sports, shared interests, links to other current curriculum areas) that interest your students
- involving students in financial literacy contexts in which percentages are important, such as saving money or budgeting.
Te reo Māori kupu such as ōrau (percent), hautau (fraction), hautaunga ā-ira (decimal fraction), and whakahekenga ōrau (percentage discount) could be introduced in this unit and used throughout other mathematical learning
- Calculators
- Computer spreadsheets
- One hundred squares (Copymaster One)
- Plastic containers or jars (large enough to hold the coloured cubes in session 2)
- Unifix, multilink cubes, (coloured counters will suffice)
- Deci-links, deci-cubes, deci-pipes, or paper tape and metre rulers, or 1 metre lengths of square dowel and orange and white Cuisenaire rods (optional)
- Brochures and examples of ‘shopping percentages’ from the media (for session 4)
Pre-prepared spreadsheets and copies for students (for session 5)
Session 1
Today we explore the relationship between percentages and fractions.
- Ask your students what 50% means. Many of them will know that 50% is equivalent to one-half and be familiar with “fifty-fifty” referring to an even chance. Ask them what they think the % sign means. Point out, if necessary, that the sign is derived from the symbol /, meaning "out of", and the two zeros from one hundred. Ask where in real life the word “per” is encountered. Students might offer ideas such as kilometres or minutes per hour, the cost of a meal per person, and dollars per litre or kilogram.
- Generally speaking, in mathematics “per” refers to a uniform rate, meaning “for every”. 40% means 40 measures for every 100 measures. The measures refer to the same unit, so percentages connect to ratios. If a student gets a ratio of 60 correct to 40 wrong in a test (60:40) they get 60% correct, since there are 60 correct answers in every 100 questions. Explain this to your students, with reference to the contexts that they have listed in discussion.
- Ask students to fold or shade a one-hundred (10 x 10) square (Copymaster One) in half and check that the area of one-half of the square is 50 out of 100. Represent this with a double number line and a place value table:
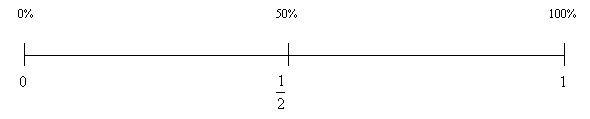

You may need to revisit a material model of decimal place values, such as deci-lengths or decimats to show why 50 hundredths equals 5 tenths. - Ask the students to predict what one-quarter and three-quarters will be as percentages. Have them fold or fold the 10 x10 square paper and then open it up to check the areas taken up by these fractions. Add the fraction to percentage conversions to the number line and place value table:
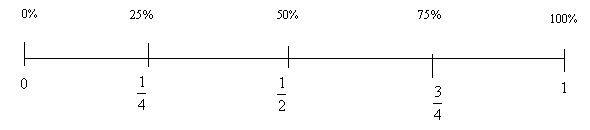

- The fractions ½ and ¼ form the start of an interesting progression.
Ask students to predict what fractions and percentages occur if the halving continues.
What is half of one quarter?
What is one eighth as a percentage? (Half of 0.25 equals 0.125 or 12.5%)
Deci-lengths or deci-pipes are useful to show the halving.
Extend the pattern to sixteenths. - Write the following fractions on the board and ask the students to express each of the fractions as percentages and decimals. Encourage them to use any representation (100 square, double number line, place value table) that they think will be helpful.
1/5, 3/5, 3/2 (1 1/2), 9/4 (2 1/4), 1/10, 1/8 - After a suitable time, discuss students’ solutions. Highlight strategies used, such as:
- Non-unit fractions as iterations (cumulative copies) of unit fractions, such as 1/5 = 0.2 = 20% so 3/5 = 0.6 = 60%
- Fractions with numerators greater than the denominator are greater than one so the percentage is greater than 100%, for instance, that 3/2 = 150%.

- Use of equivalent fractions, like; 1/5 = 2/10 = 20/100 = 20%.
- Use of double number lines as above.
- Use of ratio tables:
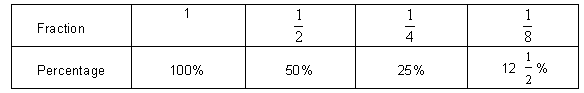
From this table we see that 1/8 = ½ x 25% = 12.5 %. - Use of calculators to check predictions developed by other means. For example, to find the percentage of 3/4 calculate 3 ÷ 4 = 0.75 = 75%. Scientific calculators have a S↔D button that changes decimal form to fraction form and vice versa.
- To consolidate students’ ability to convert from fractions to percentages and vice versa give them the following percentages to convert to fractions:
- 60%, 90%, 37.5%, 175%, 250%, 35%
Students may use any of the previously-introduced strategies to solve these problems.
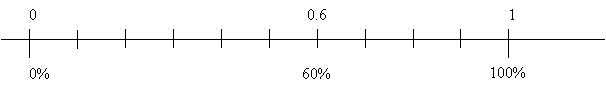
- Provide students with time to summarise the key mathematical understandings and ideas that have been covered in the session.
Session 2
In this session students solve percentage problems using a range of strategies and share those strategies.
- Revise what key mathematical content was introduced in the previous session. Look for students to recall key fraction-decimal-percentage relationships (e.g. around 50%, 25%, 75&, 100%) and those relating to more complex fractions (e.g. 1 ½, ⅛, 9/4). Look also for students to identify efficient methods for expressing fractions as percentages and decimals (e.g. double number lines, one-hundred square, ratio table, place value table). Make a note of any gaps in students’ knowledge and address these, either throughout this session or in a small-group session.
- Give the students the following problem to solve. Change the context of the problem to reflect your students’ interests and the current learning climate.:
Tāmati is trying to work out the number of goals scored by the Northern Mystics in a netball game against the Southern Steel. His sister tells him that the Northern Mystics scored 25% of the goals. The total number of goals scored throughout the game, by both teams, was 48. How many goals did the Northern Mystics score? - Let the students solve the problem in small co-operative groups and gather the class together to share strategies. Key strategies are:
- Use fractional equivalents to simplify the problem: 25% is equivalent to 1/4 so the problem becomes 1/4 x 48. Note that x means "of’’ in this case, as in "one-quarter of forty-eight."
- Use the double number line or ratio table to model the problem:
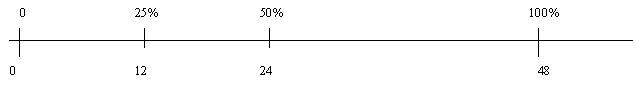

- Pose other similar problems such as:
Tipene helps his Uncle Kahu check the kōura pots in the boat. He is allowed to keep 20 % of the kōura they catch. One day Tipene and Kahu catch 25 kōura. How many kōura is he allowed to keep? - Set up the following puzzles using coloured cubes and opaque plastic jars. Tell the students that they need to work out how many cubes of each colour are in the jars. Stress the need to record their solutions:
Jar A: 30 cubes, 50% yellow, 20% green, 30% blue (15 yellow, 6 green, 9 blue)
Jar B: 36 cubes, 25% red, 75% blue (9 red, 27 blue)
Jar C 20 cubes, 20% black, 5% blue, 50% green, 25% yellow (4 black, 1 blue, 10 green, 5 yellow)
Jar D: 16 cubes, 12.5% white, 37.5% red, 50% orange (2 white, 6 red, 8 orange)
Jar E: 60 cubes, 10% yellow, 20% blue, 30% green, 40% red (6 yellow, 12 blue, 18 green, 24 red) - Gather the class to discuss their strategies for finding common percentages of amounts. Possibilities might include:
- Change the percentage to a simple fraction, e.g. 25% = ¼.
- For multiples of 10%, find 10% first through dividing by 10.
- Challenge the students to make up their own percentage jar problems for others to solve. Whilst students work on this task, you could engage with small groups of students, or individuals, to address any identified gaps in knowledge.
Session 3
In this lesson students use the percentage key on the calculator to solve problems. Encourage your students to justify the reasonableness of the answers that they get.
- Revise what key mathematical content was introduced in the previous session. Look for students to identify common percentages of amounts (e.g. 50% of 30, 10% of 60) and for them to identify efficient strategies for finding these percentages (e.g. using fractional equivalents to simplify the problem, using a double number line or ratio table, changing the percentage to a simple fraction, using multiples of 10%). Make a note of any gaps in students’ knowledge and address these, either throughout this session or in a small-group session.
- Ask the students if they know how to work out 25% of 28 using a calculator. Use a virtual four function calculator on screen so everyone can see. Key in 28 x 25%. Note that the factors are reversed in order, just like 3 x 5 = 5 x 3.
- Challenge students to find 40% of 35 by first estimating and then performing the operation on the calculator (35 x 40%.)
- Pose this problem: "Is 50% of 25 more, less, or the same as, 25% of 50?" Tell the students that you want them to explain their answers. Discuss the models that students use to solve the problem: Examples might include:
- use of equivalent fractions:
50% is 1/2, so 50% of 25 is one-half of 25;
25% is 1/4, so 25% of 50 is one-quarter of 50;
Since 50 is twice as much as 25, and one-quarter is half of one-half, the answers must be equal (doubling and halving argument); - use of operational order:
50 x 25% gives the same result as 25 x 50% as only the order of the factors is changed. This argument is not strictly correct since 50 x 0.25 is not the same operation as 25 x 0.5. - use of matching double number lines:
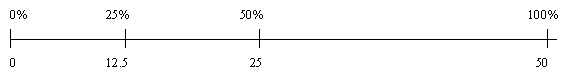
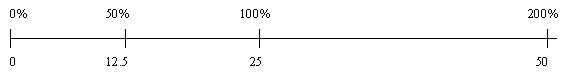
- use of equivalent fractions:
- Pose problems like those below. Tell the students that they can use a calculator if they wish but suggest that thinking about each problem may be a more beneficial first step. Note that the problems involve unknown multiplicands and multipliers, and students are likely to employ systematic trial and error strategies at first.
- 25% of what number is 12? (25% x □ = 12) (Answer: 25% of 48)
- 40% of what number is 14? (40% x □ = 14) (Answer: 40% of 35)
- What percentage of 28 is 21? (□% x 28 = 21) (Answer: 75% of 28)
- What percentage of 18 is 6? (□ %x 18 = 6) (Answer: 33.33% of 18)
- Share the strategies that students use to solve these problems. Continue to describe the strategies using common language like, "Change to equivalent fractions", "Use double number lines", and "Use tidy or unit fractions".
- An example of using tidy fractions is to solve "40% of what number is 14", using the fact that 20% or one-fifth must be 7. Since 2/5 of the number equals 14, 1/5 must be 7, and 5/5 must be 5 x 7 = 35.
- An example of using a double number line is shown below to answer “What percentage of 18 is 6?” Since 3 x 6 = 18, 6/18 = 1/3 and the percentage for 1/3 equals 33. 33%
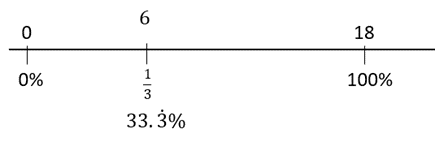
- Students might enjoy making up problems of these types for others to solve.
- Pose contextual problems where the unknown is at the start of the equation or is the whole set. For example:
Hirini gives 40% of his marbles to Melanie. He still has 21 marbles left. How many marbles did he have to start with?
Sione uses 45% of his free call minutes for this month in the first week. He has only 88 minutes left. How many free minutes does he get on his mobile plan each month?
Session 4
In this session students apply their knowledge of percentages to solve shopping problems.
- Tell the students that they now have enough tools to attempt some problems that occur in real life and involve percentages. Point out the many shops identify the amount of discount in a sale in terms of percentage off. Consider the example of a 25% off sale:
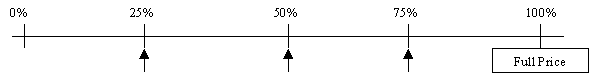
Ask the students which arrow they think matches what you would pay in a 25% off sale. Look for explanations like, "You would pay 75% of the price since 100% - 25%= 75%". - Move to specific examples from a 25% off sale. Use examples from sales brochures/media/online sources where possible, though you may wish to round the prices for easier calculation at this stage. Get the students to work out their solutions in any way they wish and share their strategies with the whole class. Here is the example of an article costing $34 at normal price:

- Provide the students with some advertising materials from shops and tell them that they can choose five articles to purchase from the brochure they receive. Tell them that the store is having a 30% off sale and they must work out what the discounted price will be. You might relate this to an engaging and relevant context - such as food to buy for a class party, headphones, books, or devices for the classroom, or gear for the sports shed. Before beginning, ask students if they can think of a way to estimate the sale price easily. Some may suggest that 30% is close to one-third and that an easy estimate is to take one-third off the price. An article that normally cost $18 would now cost about one-third ($6) less, that is, $12. Others may suggest using 10% as a benchmark and subtracting 3 amounts of 10% off the price.
- As students work, roam the room to look for the following:
- Do they have a sense of size for what amount is left after 30% is removed?
- Have students completed both operations? (i.e. finding 30% and subtracting it from 100%)
- Do they understand that removing 30% results in 70% remaining?
- Do they use 1/3 and 1/10 as benchmarks to check the answers are reasonable?
- Can they use a calculator to find the answer, as a way to check?
- When the students have had sufficient time to work on these problems, put them in pairs to check each other’s calculations. You may wish to show them how the problems can be solved on a calculator. For example, the price of a $72 article could be worked out by keying in 72 x 70% (50.4). Be sure to ask for the interpretation of 50.4 in terms of the context ($50.40).
To conclude the session, pose this problem. "Suppose you have $1000. You want to buy as many computer games as you can. Normally they cost $100 each. How many can you buy with no discount, 10% discount, 20% discount, 30% discount, etc? What do you notice about the number of games you can buy as the discount gets greater?" Suggest to the students that they may want to use a table or graph to record their findings.
Discount (%) Number of items 0 10 10 11.11111111 20 12.5 30 14.28571429 40 16.66666667 50 20 60 25 70 33.33333333 80 50 90 100 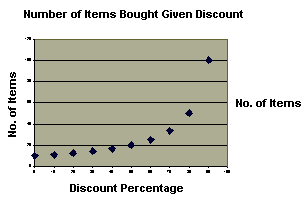
Students may notice that the impact of discount is not linear. For example, a purchaser gets twice as many of an article at 70% discount as they do at 40% discount.
Session 5
In today’s session we explore the use of percentages through banking problems.
- Ask:
Why is it important to save money?
Is it worth it to save money or should you just spend it?
How does the bank reward you for leaving your money with them?
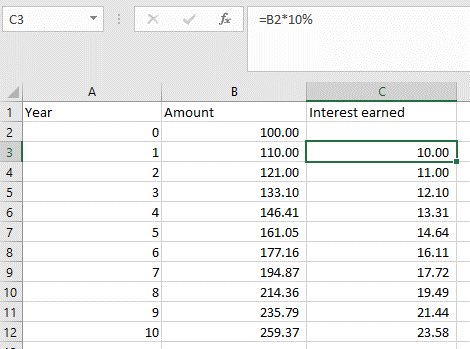
Students may or may not know about compound interest. You might demonstrate what an interest rate of 10% per annum is like. Put $100 into a container (Material Master 4-9). Each time a year passes, the bank adds 10% or 1/10 of the amount to the account.
After 1 year there is $100 + $10 = $110 in the account.
After 2 years there is $110 + $11 = $121 in the account.
What will happen at the end of Year 3?
After 3 years there is $121 + $12.10 = $133.10 in the account. - Use a spreadsheet to show how the amount in the account grows at 10% interest per annum. Ask students to predict the amount at the end of 10 years before ‘filling down.’
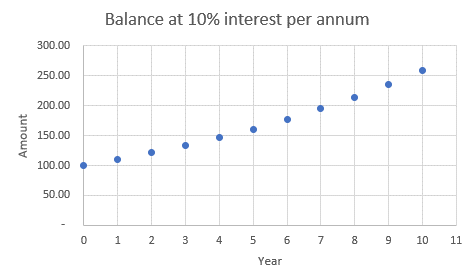
- Graph the relation between Year and Amount to see a pattern.
What do you notice about the amount as the years go by?
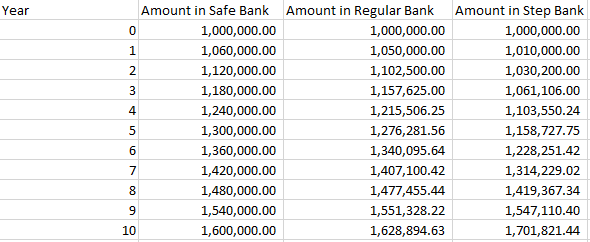
- Motivate your students. Tell them that they have $1 000 000 to invest and they must leave the money invested for ten years. There are three other investment options for them:
SafeBank will pay you $60 000 each year for all ten years that your money is with them.
RegularBank will pay you 5% compound interest at the end of every year. That means the 5% you earned in the year before will also earn interest.
StepBank will pay you 1% compound interest at the end of the first year, 2% at the end of the second year, 3% at the end of the third year, and so on until they pay 10% at the end of the tenth year.
Which bank will give you the most money at the end of ten years? - Support students to use a computer spreadsheet. Using formulae and the fill down function with a spreadsheet can save time and effort, and students can do ‘if-then’ analyses by changing the interest rate and beginning amount. If calculators are available, support students to organise their calculations in a table to help them see patterns. Note that using the formula =D2*(1+A3/100) in cell D3 (Year 1 for Step Bank) is a quick way to adjust the interest rate each year.
- Ask the students to explain why they think some investment schemes offered better returns than others. The effect of compound interest can be demonstrated by getting them to graph the returns of each investment by year.
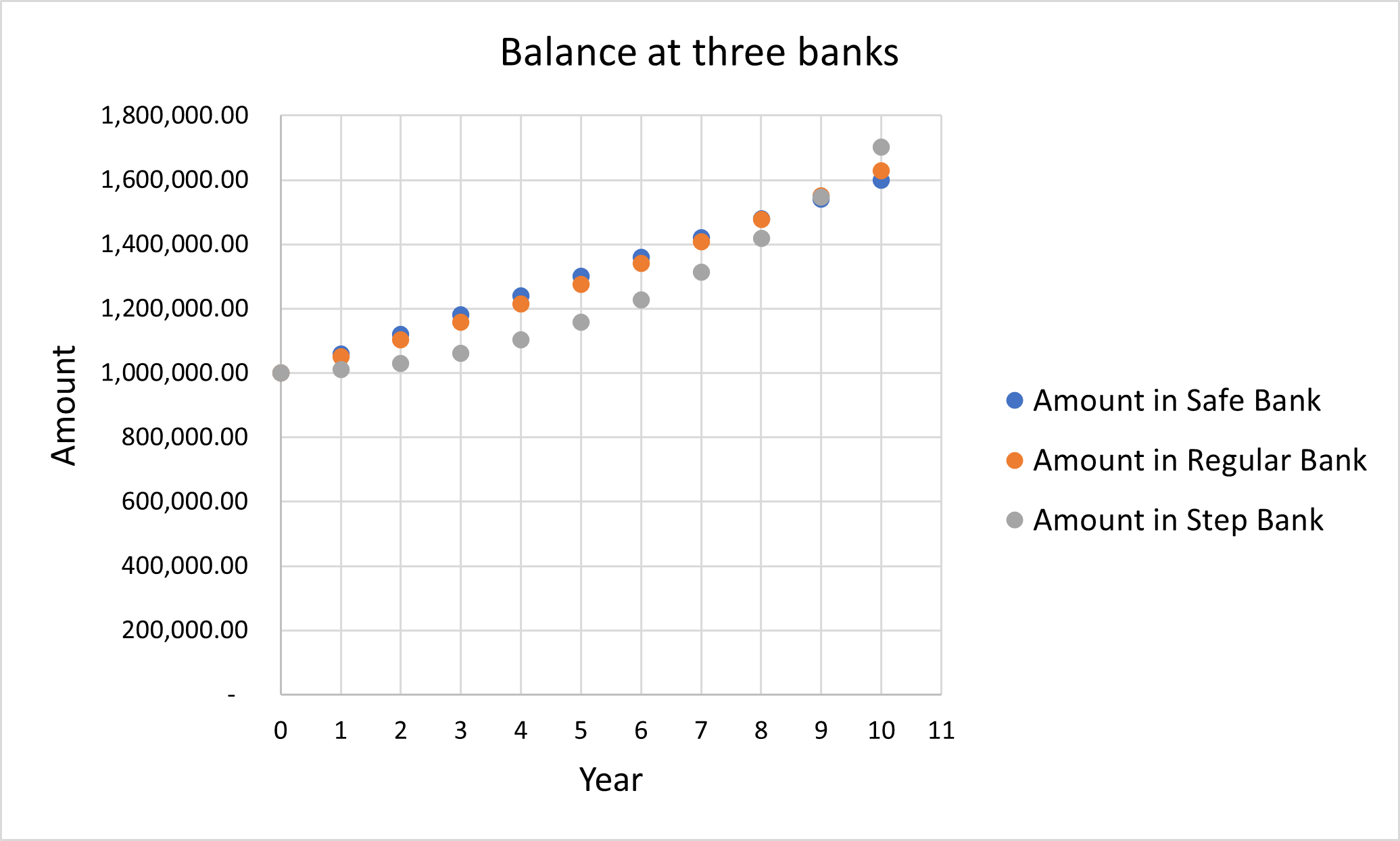
- Students might wish to investigate different investment deals that are available from local banks. These might include fixed and flexible interest rates.
Dear family and whānau
In maths this week we have explored the connections between percentages, decimals, and fractions. We have focused on strategies for solving problems involving percentages and applying these strategies to real life contexts.
At home this week we would like your child to find examples of percentages in some form of media (e.g. the newspaper, on TV, in an online advertisement, in a magazine). They should use their knowledge of percentages to make sense of the item. We would like them to write a brief explanation to accompany the item and bring this to class to share.