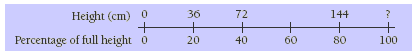Fully Grown

This context is usually of great interest to students. It is important to point out that the chart is about likely height and that, in reality, an individual’s fully grown height can be quite different from what is predicted here.
Students should try to answer questions 1 and 2 without a calculator. A calculator could be used for questions 3 and 4.
Have your students work in pairs. Ask them to examine David’s strategy and try to explain to their classmate the reason for each step. Get them to write down the reasons, like this:

Challenge your students to solve question 1 using David’s strategy; it reinforces important ideas about percentages

Another, more familiar strategy is a double number line. Students can enter the information they have and then extend the pattern to find the information they need:

Question 2 is a simple step from question 1. Now that David’s likely adult height has been determined, it should be halved to get an estimate of what his height would have been at age 2.
Question 3 also depends on the students working from a correct answer to question 1. If students are using calculators, get them to enter 85% as 0.85 instead of using the percentage key. Many calculators do not have percentage keys (because they are completely unnecessary), and students who use them are unlikely to understand what is going on mathematically.
Each of the calculations in question 3 can be done without a calculator, and you could challenge your students to do this, either before or following solution by calculator. Here is a possible line of reasoning for the first part: “We know from question 1 that David is currently 144 cm tall, which is 80% of his likely adult height. From our answer to the same question, we know that his likely adult height is 180 cm. 10% of 180 is 18 cm, which means that 5% of 180 is 9 cm.  144 + 9 = 153 cm.”
Question 4 is challenging, so focus on finding an equation that will lead to the solution. The students can then use a calculator to solve the problem. Angie’s adult height is likely to be 178 cm (2 cm shorter than her brother). She is David’s twin, so her age must now be 10. According to the chart, her present height is 86% of her likely adult height. So the equation is: 0.86 x 178 = . When they have solved the equation, the students need to remember to compare their answer with 144 cm (David’s present height) to see what the difference in height should be.

Answers to Activity

1. 180 cm (1.8 m).
If 144 cm is 80% of David’s adult height, 10% must be 144 ÷ 8 = 18 cm, so 100% must be 18 x 10 = 180 cm.
2. 90 cm (0.9 m)
If 180 cm is David’s likely adult height, his likely height at age 2 was 50% of this.
50% of 180 = 90 cm.
3. 153 cm at 12 yrs (85% of 180)
165.6 cm at 14 yrs (92% of 180)
178.2 cm at 16 yrs (99% of 180)
4. Angie is 9 cm taller than David.
Fully grown, David is likely to be 180 cm, so Angie’s adult height is likely to be 178 cm. At age 10, her height should be 86% of her adult height, that is, 86% of 178. 0.86 x 178 = 153 cm, which is 153 – 144 = 9 cm taller than David is right now.