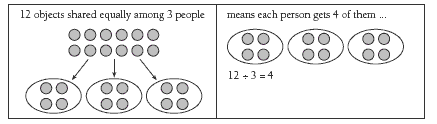Divided We Stand

This activity focuses on the number properties that are useful in solving equal-sharing and equal-sets division problems.
The introductory example starts with a total set of 72 objects and shows two possible ways of arranging the objects in smaller sets. Students will know how to express relationships of this kind as multiplications, in the form 9 x 8 = 72. In this activity, they learn that such relationships may equally well be expressed as divisions, in the form 72 ÷ 8 = 9.
You may find it useful to get your students to work initially with a smaller total set (such as 12) and to consider ways of sharing the set equally. For example:

More generally, we can say that if there are a objects shared equally among b people, each person gets c of them (a ÷ b = c).
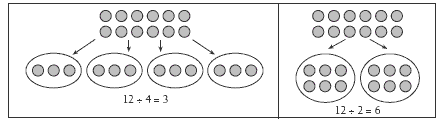
The picture also shows that 3 sets of 4 can be made from 12 objects. The answer to the question “How many sets of 4 can be made from 12?” can be written as 12 ÷ 4 = 3, meaning, in terms of the picture above, that 3 people would each get a set of 4. (Alternatively, the answer to “How many sets of 3 can be made from 12?” can be written as 12 ÷ 3 = 4.) It is very important that students learn that the division sign can be interpreted as either “split equally between” or “split equally into sets of”. Using algebraic notation, we can say that if a ÷ b = c, then a ÷ c = b.
In summary, and using a set of 40 this time, if 40 ÷ 8 = 5, then 40 ÷ 5 = 8, 8 x 5 = 40, and 5 x 8 = 40. Expressed algebraically, if a ÷ b = c, then these three other statements are also true: a ÷ c = b, b x c = a, and c x b = a.
In parts a and b of question 1, students explore the important relationship discussed above, and in part c they are reminded that an inverse relationship exists between the number of sets and the number of objects in each set. They will find this relationship useful when doing the later questions.
In question 2, students explore some strategies for making division calculations. You could introduce the ideas using examples such as the following:
Consider the connection between 12 ÷ 4 = 3 and 12 ÷ 2 = 6 as cases of equal sharing:

When 12 objects are shared into 2 equal sets, those sets contain twice as many objects as would be the case when 12 objects are shared into 4 equal sets.
If these sharing cases are written as multiplications, 4 x 3 = 12 and 2 x 6 = 12, students should recognise the doubling and halving that is going on here.
Strategies that make use of inverse relationships (especially doubling and halving and thirding and trebling strategies) can be used to simplify many division problems. For example, if there are a objects split equally into b groups and the number of objects in each group is c:
• halving the number of groups doubles the number of objects in each group (a ÷ b/2 = 2c)
• thirding the number of groups trebles the number of objects in each group (a ÷ b/3= 3c).
It is also possible to multiply or divide both the total number of objects a and the divisor b by the same amount without affecting the result. This fact can be used as a strategy for making division problems easier: the problems 48 ÷ 16 =, 24 ÷ 8 = , and 12 ÷ 4 = all have the same answer, 3.
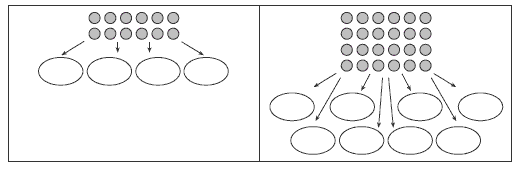
To help your students see the reason for this, have them explore the following pair of diagrams. Ask How are the diagrams related, and how many objects will end up in each group in each case?

If 12 objects are shared equally into 4 groups, there will be 3 objects in each. If twice as many objects are shared into twice as many groups, there will still be 3 objects in each. Expressed algebraically, if a ÷ b = c, then 2a ÷ 2b = c, 3a ÷ 3b = c, and so on.
However, the multiplier for both numbers (objects and groups) doesn’t have to be a whole number. It can be a fraction, with the result that both numbers get smaller and the answer is easier to calculate. For example, 72 ÷ 24 = has the same answer as 12 ÷ 4 = . Both 72 and 24 have been multiplied by one-sixth, which is the same as dividing both by 6. Expressed algebraically, if a ÷ b = c, then a/2 ÷ b/2 = c, a/3 ÷ b/3 = c, and so on.
Question 3 is ideally suited to discussion in small groups. The students think about the thought processes being used and then replicate those processes using their own choice of numbers.
Question 4 deliberately uses larger numbers to ensure that students will have to simplify them using a strategy of the kind described above.
Question 5 provides a check that the students really understand what they are doing.

Imaging

It is important that students understand the structure behind the number properties rather than just recognise and follow patterns. Have them represent each division problem, using materials so that they make the connections between words, symbols, and quantities. Interlocking cubes are ideal for this purpose.
For example, here is a model for 24 ÷ 6 = 4 as “equal sharing”:
Starting Starting with this 24-cube model, have your students pose new sharing questions (predictive questions) and then anticipate how they would need to alter the blocks to model the new outcome. For example, “How would I change this into 24 ÷ 3 = ?” “What would 24 ÷ 12 = look like?” Ensure that your students record the results with a diagram and an equation.
Asking themselves predictive questions encourages students to image the materials. Imaging is an important bridge between the concrete (materials) and the abstract (number properties).
Taking the ideas further
While simple examples like this are useful in the Using Materials and Using Imaging stages of the Numeracy Development Project (NDP) teaching model, they are unlikely to sell the power of the number properties to students. It is vital that the difficulty level is raised to the point where the power of the number properties becomes obvious and is essential in solving calculations.
For example, by posing the problem If there are 144 lollies to be shared among 16 people, how many lollies does each person get?, you will force the students to choose a strategy that will make the problem manageable. In this case, halving both numbers reduces the problem’s complexity to the point where it can be solved by the use of basic facts (144 ÷ 16 = 72 ÷ 8 = 9).
By carefully selecting the numbers involved in problems, you can ensure that some strategies will be more efficient than others. Efficiency relates to the number and complexity of the steps involved in the calculation. For example, the problem 252 ÷ 6 =  might be solved in either of these two ways:
either 240 ÷ 6 = 40; 252 – 240 = 12, 12 ÷ 6 = 2; 40 + 2 = 42;
or 252 ÷ 6 = 126 ÷ 3 = 42.
Although both strategies use place value understanding, the second (halving both numbers) is clearly more efficient. It is important that students explore which strategy or strategies is/are most efficient for any given problem.
Another useful extension question is 279 ÷ 9. Students may initially look at using one of the strategies in the activity but will hopefully recognise that in this case, place value partitioning is best: 270 ÷ 3 = 30; 9 ÷ 9 = 1; 30 + 1 = 31, so 279 ÷ 9 = 31. By inspection, they know that 279 is divisible by 9 because the digital root is 9 (2 + 7 + 9 = 18; 1 + 8 = 9).

Answers to Activity

1. a. 72 ÷ 8 = 9, so 72 ÷ 4 = 18.
b. 72 ÷ 8 = 9, so 72 ÷ 9 = 8.
c. 8 x 9 = 72, so (using tripling and thirding)
24 x 3 = 72.
2. a. Some equations for 56 are:
56 ÷ 8 = 7,
so 56 ÷ 7 = 8,
so 56 ÷ 14 = 4,
so 56 ÷ 4 = 14,
so 56 ÷ 2 = 28,
so 56 ÷ 28 = 2.
Or: 56 ÷ 1 = 56, so 56 ÷ 56 = 1.
b. Some equations for 48 are:
48 ÷ 6 = 8,
so 48 ÷ 8 = 6,
so 48 ÷ 4 = 12,
so 48 ÷ 12 = 4,
so 48 ÷ 24 = 2,
so 48 ÷ 2 = 24;
48 ÷ 3 = 16,
so 48 ÷ 16 = 3.
Or: 48 ÷ 1 = 48, so 48 ÷ 48 = 1.
c. Some equations for 64 are:
64 ÷ 8 = 8,
so 64 ÷ 4 = 16,
so 64 ÷ 2 = 32,
so 64 ÷ 32 = 2,
so 64 ÷ 16 = 4
(or starting with their reverse equations, for example, 64 ÷ 16 = 4). Or: 64 ÷ 1 = 64, so 64 ÷ 64 = 1.
d. Some equations for 96 are:
96 ÷ 8 = 12,
so 96 ÷ 12 = 8,
so 96 ÷ 6 = 16,
so 96 ÷ 3 = 32;
96 ÷ 4 = 24,
so 96 ÷ 2 = 48
(or starting with their reverse equations, for example, 96 ÷ 48 = 2).
e. Some equations for 78 are:
78 ÷ 2 = 39,
so 78 ÷ 39 = 2;
78 ÷ 3 = 26,
so 78 ÷ 6 = 13,
so 78 ÷ 13 = 6.
f. Some equations for 84 are:
84 ÷ 4 = 21;
so 84 ÷ 12 = 7,
so 84 ÷ 6 = 14,
so 84 ÷ 3 = 28
(or their reverse equations).
3. a. Matthew’s idea: Double the divisor gives half the answer. Examples will vary. An example of doubling the divisor is: 64 ÷ 8 = 8, so 64 ÷ 16 = 4.
b. Laurel’s idea: The divisor and the answer are both factors of the first number. Examples will vary. One example (using the basic fact 5 x 9 = 45) is: 45 ÷ 5 = 9, so 45 ÷ 9 = 5.
c. Taylah’s idea: Halving the number being divided and the divisor will give the same
answer. Examples will vary. One example is: 42 ÷ 14 = 3, so 21 ÷ 7 = 3.
d. Quinten’s idea: Treble the divisor, and the answer is of the first answer. Examples
will vary. One example is: 36 ÷ 4 = 9, so 36 ÷ 12 = 3.
4. The choice of two strategies will vary, and so will the reasons given. Some examples are:
a. For 112 ÷ 8 =, you could use:
56 ÷ 4 = 14 and 28 ÷ 2 = 14 (Taylah’s strategy). Another strategy that works well here, halving the number being divided gives 2 times the answer, is a variation on Matthew’s strategy: 56 ÷ 8 = 7, so 112 ÷ 8 = 14. To use this strategy in this problem, you need to know 8 x 7 = 56.
b. For 140 ÷ 5 = , you could use:
140 ÷ 10 = 14, so 140 ÷ 5 = 28 (Matthew’s strategy); or
280 ÷ 10 = 28 (reversing Taylah’s strategy: doubling both instead of halving). Both
work well as long as you know how to use your 10 times table in division.
c. For 81 ÷ 3 = , you could use:
81 ÷ 9 = 9, so 81 ÷ 3 = 27 (from 9 x 3 = 27) (reversing Quinten’s strategy); or 81 ÷ 6 = 13.5 and 13.5 x 2 = 27, so 81 ÷ 3 = 27 (Matthew’s strategy). The first
way is easier for this problem because it uses the 9 and 3 times tables and whole numbers.
d. For 88 ÷ 4 = , you could use 44 ÷ 2 = 22, so 88 ÷ 4 = 22 (Taylah’s strategy); or
88 ÷ 8 = 11, 11 x 2 = 22, so 88 ÷ 4 = 22 (Matthew’s strategy). Both ways work well for this problem.
5. Problems will vary. They should all have an answer of 15. The equations used could include 30 ÷ 2 = 15, 120 ÷ 8 = 15, or 15 ÷ 1 = 15.