Digital Dilemmas

In this activity, there are lots of opportunities for students to apply advanced multiplicative strategies as they explore the relationship between two amounts of memory allocated to photos of different formats on a digital camera.
Students need to be at least advanced multiplicative thinkers (stage 7) to solve all the calculations in this activity mentally. Students who are at stage 6 could do the activity using a calculator where necessary.
You may need to explain that kilobyte (kb) and megabyte (Mb) are units that measure how much information can be stored on a computer. A kilobyte is approximately 1 000 bytes, and a megabyte is approximately 1 000 000 bytes.
You could get the students interested in this activity by letting them take some photos on a digital camera, experimenting with the resolution setting, and comparing the results. Talk about how the photos are stored on a memory card (some cameras use memory sticks or disks) and how the higher the resolution, the greater the memory used by each photo. Extra-wide photos automatically have a higher resolution so that they can be printed bigger without looking fuzzy, but this means that they take up more memory.
Promote algebraic thinking in this activity by focusing discussion on how the numbers relate to each other and by getting the students to use patterns to predict answers.
Many of the problems in this activity look daunting but can be solved quite easily using number sense strategies. Identify key number facts that may prompt the students to use their number sense strategies by asking:
Question 1a: What’s double 125? Double 250? Double 500? Can you use the doubling we’ve just done to help you work out what 1 000 ÷ 125 is? “There are 2 lots of 125 in 250, so there are 4 lots of 125 in 500 and 8 lots of 125 in 1 000. 1 000 ÷ 125 = 8.” Write the facts on the board as the students identify them so that they can refer back to them.
Can you use the fact that 1 000 ÷ 125 = 8 to work out 3 000 ÷ 125? “If there are 3 thousands and each one has 8 lots of 125, there must be 3 x 8 = 24 lots of 125 altogether, so 3 000 ÷ 125 = 24.”
Question 1b: What’s double 375? Double 750? Double 1 500? Can you use the doubling we’ve just done to help you work out what 3 000 ÷ 375 is? “There are 2 lots of 375 in 750, so there are 4 lots of 375 in 1 500 and 8 lots of 375 in 3 000. 3 000 ÷ 375 = 8”
Question 2: How many times does 125 go into 375? (3 x 125 = 375) If you know that 3 x 125 = 375 and that 2 x 375 = 750, how many lots of 125 are there in 750? “There must be 6 x 125 because every 375 has 3 lots of 125 and there are 2 lots of 375.
 x 125 = 2 x 375
= 2 x (3 x 125)
= 6 x 125”
If you take 1 lot of 375 away from 3 000, how much is left? Encourage the students to use an empty number line if they need to. Two possible strategies are:

• Using place value partitioning: 3 000 – 300 = 2 700, 2 700 – 75 = 2 625

• Using tidy numbers and compensating: 3 000 – 400 = 2 600, 2 600 + 25 = 2 625

You’ve worked out that 3 000 – 375 = 2 625. You know that 3 x 125 = 375. You also know that 3 000 ÷ 125 = 24. Can you use those facts to help you work out how many lots of 125 there are in 2 625? (375 [or 3 lots of 125] were taken away from 3 000 to get 2 625. If there are 24 lots of 125 in 3 000 altogether and you’ve already taken away 3 of them, there must be 21 lots of 125 left. [24 x 125] – [3 x 125] = 21 x 125)
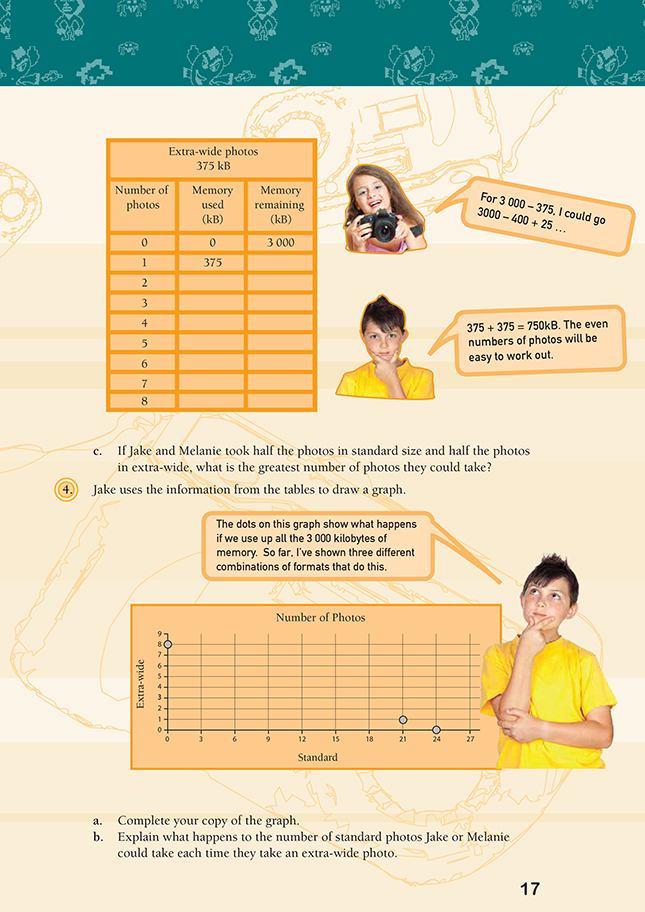
In question 3, encourage the students to complete the tables using strategies such as known facts, tidy numbers and compensating, place value partitioning, and doubling. Remind them of key facts (such as 8 x 125 = 1 000, 24 x 125 = 3 000, 8 x 375 = 3 000, and 3 x 125 = 375) that they could use to help them. Encourage the students to compare the two tables and to make links between the numbers of extra-wide and standard photos and the memory used.
Some students may need to use a calculator at times during this activity so that they can concentrate on the algebraic aspects. Encourage them to evaluate for themselves when they need to use a calculator by asking them to look carefully at the problem to see whether they know a strategy they could try first. Remind them that number sense is very important when using a calculator because they need to check by “backwards estimation” that the answer they get is sensible and not the result of an incorrect entry.

Extension

The students may like to explore the relationship between resolution and memory using the school’s digital camera.

Answers to Activity

1. a. They need to find a solution for 3 000 ÷ 125 = . One way to solve this is
to reverse the problem, making it multiplication, and then perhaps use a
doubling strategy:
 x 125 = 3 000. 2 x 125 = 250,
4 x 125 = 500, 8 x 125 = 1 000. Then they could triple both sides to make
(3 x 8) x 125 = 3 x 1 000 or 24 x 125 = 3 000. 3 000 ÷ 125 = 24, which
means that 24 standard photos could be stored on the camera.
b. They need to find a solution for
3 000 ÷ 375 = . One way to solve this is to reverse the problem to make it a
multiplication:  x 375 = 3 000. Tidy numbers might help them estimate, and if
they realise that 8 x 400 = 3 200, they might try 8 as the solution. 8 x 375 = 3 000.
Another way is to double repeatedly:
2 x 375 = 750; 4 x 375 = 1 500.
1 500 + 1 500 = 3 000, so 8 x 375 = 3 000,
which means that 8 extra-wide photos would fit on the camera. Or they may realise that 375 is 3 x 125 kb. So of the 24 standard photos is 24 ÷ 3 = 8.
2. Explanations will vary. The basic equation is 2 625 ÷ 125 = . Melanie may have known that every extra-wide photo taken uses up the space needed by 3 standard photos (125 x 3 = 375) and that 24 standard photos could fit altogether if there were no extra-wide ones, so 24 – 3 = 21.
3. a. i.

ii.

b. Discussion will vary. Note the reverse order of the second table and the way each row links to its matching row in the other table.
c. 12 photos (6 of each size)
4. a.

b. Every time Jake or Melanie take an extra-wide photo, the number of standard
photos they can take decreases by 3.