Digit Shuffle

Activities One and Two

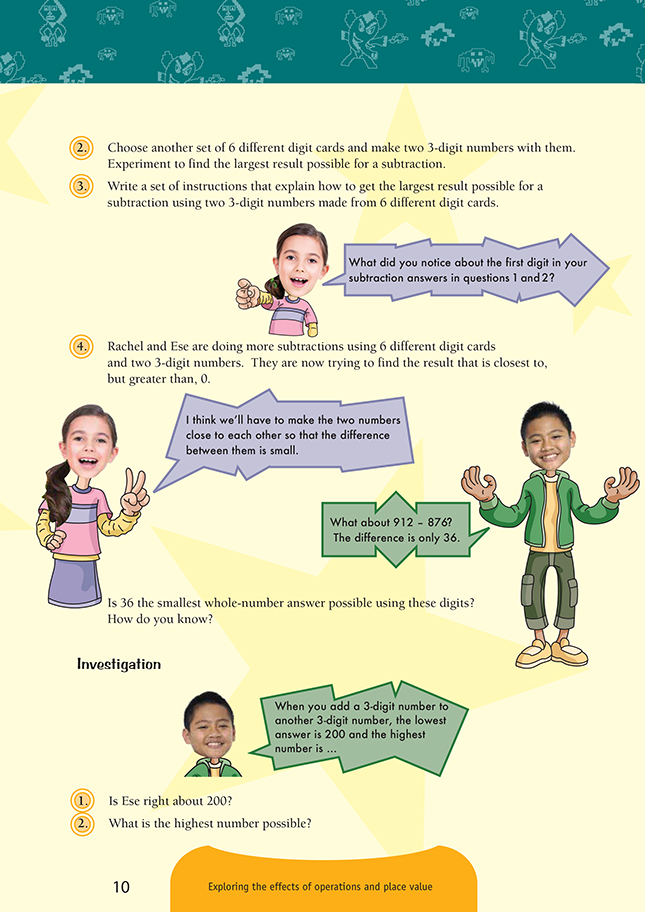
These activities are intended to reinforce the principle of place value: that the value of a digit in a number changes according to the position it is in. Students explore what effect changing the order of the digits has on the solution in addition and subtraction equations.
The students who are not confident using a variety of mental strategies to quickly add and subtract 3-digit numbers could use a calculator so that they can concentrate on the place value. They may also be more willing to experiment with moving their numbers around to create new calculations.
However, they should use the calculator as a backstop rather than automatically reaching for it every time. Encourage them to look first at the numbers in the problem and decide whether they could solve it easily in their heads. For example, Activity One, question 2, asks them to add 623 + 547, which is relatively straightforward when using a place value partitioning strategy such as 600 + 500 = 1 100, 20 + 40 = 60, 3 + 7 = 10, 1 100 + 60 + 10 = 1 170.
In Activity Two, question 4, the numbers should be close enough together for the students to be able to use an adding-on strategy. Even when the calculator is used, the students should use mental strategies to estimate whether the answer shown on the calculator is correct or whether the numbers have been entered incorrectly; just because it’s on the calculator screen doesn’t guarantee it’s right!
The questions that ask the students to write a set of instructions are ideal for promoting algebraic thinking. They are also useful for formative assessment.

Investigation

If the students have difficulties with Ese’s investigation at the end of the activity, encourage them to experiment by adding a range of 3-digit numbers together. Ask:
What’s the smallest 3-digit number possible?
What’s the largest 3-digit number possible?
Some students might be interested in posing their own follow-up investigation question, such as predicting the number of digits in the answer when adding two 4-digit numbers, subtracting a 3-digit number from a 4-digit number, and so on.
 

Answers to Activity

Activity One
1. The largest total possible is 1 827. This can be made with 973 + 854, 953 + 874, 954 + 873, or 974 + 853.
2. a. 1 170
b. 1 395
c. 4 ways: 753 + 642; 752 + 643; 742 + 653; 743 + 652
3. Answers will vary.
4. A possible set of instructions is: Put the 2 largest digits in the hundreds places of the 2 numbers. Put the 2 smallest digits in the ones places. Put the middle 2 digits in the tens places.
5. The instructions would be reversed. For example, put the 2 smallest digits in the hundreds places of the 2 numbers. Put the 2 largest digits in the ones places. Put the middle 2 digits in the tens places.
6. The largest total possible is 2 556. The smallest total possible is 774. There are lots of different ways of arranging the digits to get these totals, but the same basic rules for placing them apply.
(See the answers for questions 4 and 5.)
Activity Two
1. 531 is the largest answer possible:
987 – 456 = 531
2. Answers will vary.
3. A possible set of instructions is: Choose the 3 largest digits and make the biggest number you can by putting the biggest digit in the hundreds place and the smallest of the 3 digits in the ones place. Take the 3 smallest digits and make the smallest number you can by putting the smallest digit in the hundreds place and the largest of the 3 digits in the ones place. Subtract the small number from the large number.
4. No. The smallest possible answer is 14, given by the subtraction 712 – 698.
Investigation
1. Yes. The smallest possible 3-digit numbers you could add together are 100 + 100 = 200.
2. 1 998. (999 + 999)