This problem solving activity has a logic and reasoning focus.
Brian has a pegboard with 9 pegs in a 3 by 3 square array (see the diagram).
He also has a piece of string that he wants to put from the top left hand peg A, to the bottom right hand peg B, so that it touches all of the other pegs on the way only once.
If the string is never put diagonally between the pegs, how many different ways can Brian string up his pegboard?
- Use a systematic approach to count a set of possible outcomes.
This problem challenges students in two ways. Firstly, they are challenged to be systematic in a novel situation. This is an important aspect of much of mathematics. Many students record their working in a haphazard way as they go along. This may lead to errors when students lose track of what they have done and what they still need to do. Being systematic and careful with the recording of work is an important tool that is fundamental to all mathematics.
Secondly, this problem highlights the need to count in a situation that is new to them. Counting is a fundamental part of probability. In order to determine theoretical probabilities accurately, a knowledge of counting techniques is extremely important.
In this problem a guess and check strategy can be used. However, such an approach cannot guarantee that all outcomes have been obtained. Guess and check is nonetheless a good first strategy that will give the students an idea of the problem, along with some possible properties of the problem that they can use in a more systematic approach. However, students should be supported and encouraged to see that there is a better way to try to solve the problem. One way to do this is to help them to see where there are choices, and then to see what implications these choices have.
Once the students have the idea of being systematic in this problem, you might like encourage them further into an investigation. This might be done in several ways. One way is to look at any pair of pegs and see if they can be joined by string in a way prescribed.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Pegboards (if available - or a digital model)
The Problem
Brian has a pegboard with 9 pegs in a 3 by 3 square array (see the diagram).
He also has a piece of string that he wants to put from the top left hand peg A, to the bottom right hand peg B, so that it touches all of the other pegs on the way only once. If the string is never put diagonally between the pegs, how many different ways can Brian string up his pegboard?
Teaching Sequence
- Introduce the idea of a pegboard. Let the class play with one so that they are familiar with the apparatus.
- Introduce the problem.
Do you understand what Brian is trying to do?
Can you think of one way that might work? - Let the students work in their groups to solve the problem. You may need to help them be systematic (e.g. by drawing a diagram, constructing a table, using the materials and recording tally marks). If most of the class can only use guess and check, then it is worth gathering them all together to discuss how they might be systematic.
- Check the progress of each group. Give assistance where needed. Any group that finishes early can try the Extension problem.
- Get the students to report back to the whole class.
- Give them time to write up their method of solution.
Extension
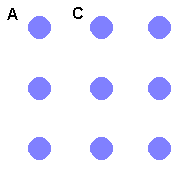
Can Brian string up his pegboard so that it starts at A and ends at C (see diagram). Remember that he is always going to make sure that the string goes horizontally or vertically between neighbouring pegs touching each only once.
Solution
To be able to do this and make sure that we don’t miss anything it is necessary to be systematic in what we do. To this end, there are a couple of things to notice straight away. First that we can start off by making a string path in either a horizontal or vertical direction from A. Because of the symmetry of the square, whatever stringing we do that starts horizontally, there is another stringing that starts vertically. We can explore the horizontal starts and then just rotate these at the end to give some more string paths. Let’s assume then that we start as in the diagram.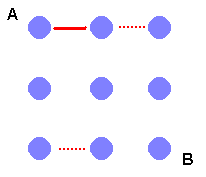
The second thing to notice is the limitations of the pegs D and E. There is only one way that the string can go round these pegs. We show this in the diagram below.
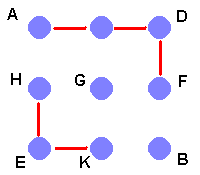
Now F can’t join up to B as we have still more pegs to go past. So F joins to G.
Then G joins H or else H is left high and dry. The only thing left is to join K and B to complete the stringing below.
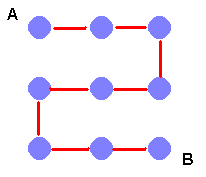
Because of the rotation we talked about earlier, there is one other stringing. It is the rotation through 45° about the diagonal from A to B. This means that there are precisely two stringings that Brian can make altogether.
Solution to the Extension
Now what can be done here? First Brian can’t join A to C as this misses out most of the pegs. So A joins H. And we still have the situation at D and E forced. So so far we have the situation below.
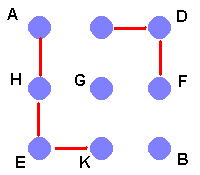
But the same thing has to happen at B as happens at D and E. This means that we can’t use the peg. We can’t join A to C in the way that we wanted.
What other pegs can A be joined to? What pairs of pegs can be joined by Brian?