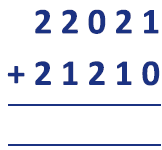This problem solving activity has a number focus.
We say that the number 1202 is a number in base 3 when we write it as 1 x 33 + 2 x 32 + 0 x 3 + 2 x 30.
This is equal to 27 + 18 + 2 = 47 in our normal base, base 10.
What is the value of the base 3 number 21021?
What is the sum of the two base 3 numbers in base 3?
Write the base 10 number 582 in base 3.
- Write numbers in base 3.
- Do arithmetic in base 3.
- Explain the "links" between base 3 and decimal numbers.
- Devise and use problem solving strategies to explore situations mathematically (be systematic).
This problem enables students to better understand our decimal system by looking at a comparable system – the base 3 system.
Students should see that numbers can be represented in more than one way. Sometimes one system has an advantage over another.
For instance base 2 is very useful in telecommunications. Electricity can be made to pulse or not to pulse through circuits. By using the pulse to represent 1 and the non-pulse to represent 0, numbers can be transmitted along a line. Once that has been done, letters can be transmitted too. This is because we can code letters by numbers. In this way the base 2 system allows us to send messages by phone lines or as radio waves.
There are other uses of bases. For instance we represent vectors in three dimensions in terms of the unit vectors i, j and k. In seven dimensions we can use seven unit vectors and so on for higher dimensions.
The base 3 system (ternary) has 3 digits: 0, 1, and 2. Your students might find it interesting to investigate other number base systems.
The Problem
We say that the number 1202 is a number in base 3 when we write it as 1 x 33 + 2 x 32 + 0 x 3 + 2 x 30. This is equal to 27 + 18 + 2 = 47 in our normal base, base 10.
What is the value of the base 3 number 21021?
Write the base 10 number 582 in base 3.
Teaching Sequence
- Introduce the problem by first talking about decimal numbers.
What is 102? How about 107?
What do the digits 1, 2 and 0 actually stand for in the number 120?
Can you expand 2376 in terms of powers of 10? - Then talk about base 3 numbers.
What is 34? How about 38?
What do the digits 1, 2, 0 actually stand for in the base 3 number 120?
Can you expand the base 3 number 21102 in terms of powers of 3?
What does the base 3 number 220011 equal in base 10? - Pose the problem and have students work on this in their groups.
- As the groups work you may need to give them simpler problems to help them to work out parts b) and c).
- Have some groups share and explain their solutions to the class.
- Allow students time to write up and to explain their solutions.
Extension
Find a way of changing any base 10 number into a base 3 number.
Solution
- 21021 = 2 x 34 + 1 x 33 + 0 x 32 + 2 x 3 + 1 = 162 + 27 + 6 + 1 = 196.
- Note that 1 + 2 = 10 in base 3 and 2 + 2 = 11. So
| 2 2 0 2 1 |
| +2 1 2 1 0 |
| 12 1 0 0 1 |
- Key numbers in base 3 are 1, 3, 9, 27, 81, 243, 729, … In other words, the powers of 3.
The biggest power of 3 less than 582 is 243 and 2 x 243 = 486 is less than 582. So the base 3 form of the number will start 2… = 2 x 35 + …
582 – 486 = 96.
81 is the biggest power of 3 less than 96.
So 582 starts 21… = 2 x 35 + 1 x 34 + …
Since 96 – 81 = 15 which equals 9 + 6,
then 582 = 2101… = 2 x 35 + 1 x 34 + 0 x 33 + 1 x 32 + 2 x 3 + 0 x 30.
Solution to the Extension
We show a particular example of a general method
3 | 582 | |
3 | 194 | 0 |
3 | 64 | 2 |
3 | 21 | 1 |
3 | 7 | 0 |
3 | 2 | 1 |
0 | 2 |
The threes on the left divide the corresponding numbers in the centre. The quotient is written in the line below and the remainder goes on the right.
Begin with 299.
3 | 299 | 3 | 299 | 3 | 299 | |||||
99 | 2 | 3 | 99 | 2 | 3 | 99 | 2 | |||
33 | 0 | 3 | 33 | 0 | ||||||
11 | 0 |
3 | 299 | 3 | 299 | |||
3 | 99 | 2 | 3 | 99 | 2 | |
3 | 33 | 0 | 3 | 33 | 0 | |
3 | 11 | 0 | 3 | 11 | 0 | |
3 | 3 | 2 | 3 | 3 | 2 | |
3 | 1 | 0 | ||||
3 | 0 | 1 |
In the first table we divide 299 by 3 get 99 (in the table) and remainder of 2 (to the right). This 2 is the last digit on the right of the base 3 form of 299. Then 3 into 99 goes 33 times (in the table) and the remainder is 0 (to the right). This remainder of 0 becomes the second digit from the right in the final base 3 form of the number. We keep going down.
This algorithm changes numbers in base 10 to numbers in base 3. Just check, 582 in base 3 is 210120 (we’ve seen that already). But 299 in base 3 is 102002.
Why does this algorithm work?
If base 3 is well understood, try working in base 4 or any other base you can think of.